1.1. The many faces of the cosmological constant

Einstein's equations, which determine the dynamics of the spacetime, can be derived from the action (see, eg. [7]):

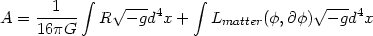(1)

where L_matter is the Lagrangian for matter depending on some dynamical variables generically denoted as . (We are using units with c = 1.) The variation of this action with respect to will lead to the equation of motion for matter (L_matter / ) = 0, in a given background geometry, while the variation of the action with respect to the metric tensor g_ik leads to the Einstein's equation

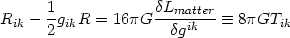(2)

where the last equation defines the energy momentum tensor of matter to be T_ik 2(L_matter / g^ik).

Let us now consider a new matter action L'_matter = L_matter - ( / 8G) where is a real constant. Equation of motion for the matter (L_matter / ) = 0, does not change under this transformation since is a constant; but the action now picks up an extra term proportional to

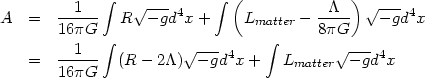(3)

and equation (2) gets modified. This innocuous looking addition of a constant to the matter Lagrangian leads to one of the most fundamental and fascinating problems of theoretical physics. The nature of this problem and its theoretical backdrop acquires different shades of meaning depending which of the two forms of equations in (3) is used.

The first interpretation, based on the first line of equation (3), treats as the shift in the matter Lagrangian which, in turn, will lead to a shift in the matter Hamiltonian. This could be thought of as a shift in the zero point energy of the matter system. Such a constant shift in the energy does not affect the dynamics of matter while gravity - which couples to the total energy of the system - picks up an extra contribution in the form of a new term Q_ik in the energy-momentum tensor, leading to:

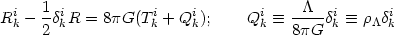(4)

The second line in equation (3) can be interpreted as gravitational field, described by the Lagrangian of the form L_grav (1/G)(R - 2), interacting with matter described by the Lagrangian L_matter. In this interpretation, gravity is described by two constants, the Newton's constant G and the cosmological constant . It is then natural to modify the left hand side of Einstein's equations and write (4) as:

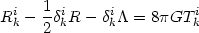(5)

In this interpretation, the spacetime is treated as curved even in the absence of matter (T_ik = 0) since the equation R_ik - (1/2)g_ikR - g_ik = 0 does not admit flat spacetime as a solution. (This situation is rather unusual and is related to the fact that symmetries of the theory with and without a cosmological constant are drastically different; the original symmetry of general covariance cannot be naturally broken in such a way as to preserve the sub group of spacetime translations.)

In fact, it is possible to consider a situation in which both effects can occur. If the gravitational interaction is actually described by the Lagrangian of the form (R - 2), then there is an intrinsic cosmological constant in nature just as there is a Newtonian gravitational constant in nature. If the matter Lagrangian contains energy densities which change due to dynamics, then L_matter can pick up constant shifts during dynamical evolution. For example, consider a scalar field with the Lagrangian L_matter = (1/2)_i ⁱ - V() which has the energy momentum tensor

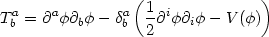(6)

For field configurations which are constant [occurring, for example, at the minima of the potential V()], this contributes an energy momentum tensor T_b^a = ^a_b V(_min) which has exactly the same form as a cosmological constant. As far as gravity is concerned, it is the combination of these two effects - of very different nature - which is relevant and the source will be T_ab^eff = [V(_min) + ( / 8 G)] g_ab, corresponding to an effective gravitational constant

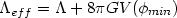(7)

If _min and hence V(_min) changes during dynamical evolution, the value of _eff can also change in course of time. More generally, any field configuration which is varying slowly in time will lead to a slowly varying _eff.

The extra term Q_ik in Einstein's equation behaves in a manner which is very peculiar compared to the energy momentum tensor of normal matter. The term Qⁱ_k = ⁱ_k is in the form of the energy momentum tensor of an ideal fluid with energy density and pressure P = - ; obviously, either the pressure or the energy density of this "fluid" must be negative, which is unlike conventional laboratory systems. (See, however, reference [8].)

Such an equation of state, = - P also has another important implication in general relativity. The spatial part g of the geodesic acceleration (which measures the relative acceleration of two geodesics in the spacetime) satisfies the following exact equation in general relativity (see e.g., page 332 of [9]):

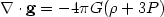(8)

showing that the source of geodesic acceleration is ( + 3P) and not . As long as ( + 3P) > 0, gravity remains attractive while ( + 3P) < 0 can lead to repulsive gravitational effects. Since the cosmological constant has ( + 3P) = - 2, a positive cosmological constant (with > 0) can lead to repulsive gravity. For example, if the energy density of normal, non-relativistic matter with zero pressure is _NR, then equation (8) shows that the geodesics will accelerate away from each other due to the repulsion of cosmological constant when _NR < 2. A related feature, which makes the above conclusion practically relevant is the fact that, in an expanding universe, remains constant while _NR decreases. (More formally, the equation of motion, d ( V) = - P dV for the cosmological constant, treated as an ideal fluid, is identically satisfied with constant , P.) Therefore, will eventually dominate over _NR if the universe expands sufficiently. Since ||^1/2 has the dimensions of inverse length, it will set the scale for the universe when cosmological constant dominates.

It follows that the most stringent bounds on will arise from cosmology when the expansion of the universe has diluted the matter energy density sufficiently. The rate of expansion of the universe today is usually expressed in terms of the Hubble constant: H₀ = 100h km s^-1 Mpc^-1 where 1 Mpc 3 × 10²⁴ cm and h is a dimensionless parameter in the range 0.62 h 0.82 (see section 3.2). From H₀ we can form the time scale t_univ H₀^-1 10¹⁰h^-1 yr and the length scale cH₀^-1 3000h^-1 Mpc; t_univ characterizes the evolutionary time scale of the universe and H₀^-1 is of the order of the largest length scales currently accessible in cosmological observations. From the observation that the universe is at least of the size H₀^-1, we can set a bound on to be || < 10^-56 cm^-2. This stringent bound leads to several issues which have been debated for decades without satisfactory solutions.

• In classical general relativity, based on the constants G, c and , it is not possible to construct any dimensionless combination from these constants. Nevertheless, it is clear that is extremely tiny compared to any other physical scale in the universe, suggesting that is probably zero. We, however, do not know of any symmetry mechanism or invariance principle which requires to vanish. Supersymmetry does require the vanishing of the ground state energy; however, supersymmetry is so badly broken in nature that this is not of any practical use [10, 11].
• We mentioned above that observations actually constrain _eff in equation (7), rather than . This requires and V(_min) to be fine tuned to an enormous accuracy for the bound, |_eff| < 10^-56 cm^-2, to be satisfied. This becomes more mysterious when we realize that V(_min) itself could change by several orders of magnitude during the evolution of the universe.
• When quantum fields in a given curved spacetime are considered (even without invoking any quantum gravitational effects) one introduces the Planck constant, , in the description of the physical system. It is then possible to form the dimensionless combination (G / c³) L_P². The bound on translates into the condition L_P² 10^-123. As has been mentioned several times in literature, this will require enormous fine tuning.
• All the above questions could have been satisfactorily answered if we take _eff to be zero and assume that the correct theory of quantum gravity will provide an explanation for the vanishing of cosmological constant. Such a view was held by several people (including the author) until very recently. Current cosmological observations however suggests that _eff is actually non zero and _eff L_P² is indeed of order (10^-123). In some sense, this is the cosmologist's worst nightmare come true. If the observations are correct, then _eff is non zero, very tiny and its value is extremely fine tuned for no good reason. This is a concrete statement of the first of the two `cosmological constant problems'.
• The bound on L_P² arises from the expansion rate of the universe or - equivalently - from the energy density which is present in the universe today. The observations require the energy density of normal, non relativistic matter to be of the same order of magnitude as the energy density contributed by the cosmological constant. But in the past, when the universe was smaller, the energy density of normal matter would have been higher while the energy density of cosmological constant does not change. Hence we need to adjust the energy densities of normal matter and cosmological constant in the early epoch very carefully so that _NR around the current epoch. If this had happened very early in the evolution of the universe, then the repulsive nature of a positive cosmological constant would have initiated a rapid expansion of the universe, preventing the formation of galaxies, stars etc. If the epoch of _NR occurs much later in the future, then the current observations would not have revealed the presence of non zero cosmological constant. This raises the second of the two cosmological constant problems: Why is it that ( / _NR) = (1) at the current phase of the universe ?
• The sign of determines the nature of solutions to Einstein's equations as well as the sign of ( + 3P). Hence the spacetime geometry with L_P² = 10^-123 is very different from the one with L_P² = - 10^-123. Any theoretical principle which explains the near zero value of L_P² must also explain why the observed value of is positive.

At present we have no clue as to what the above questions mean and how they need to be addressed. This review summarizes different attempts to understand the above questions from various perspectives.