1.2. A brief history of cosmological constant

Originally, Einstein introduced the cosmological constant in the field equation for gravity (as in equation (5)) with the motivation that it allows for a finite, closed, static universe in which the energy density of matter determines the geometry. The spatial sections of such a universe are closed 3-spheres with radius l = (8 G _NR)^-1/2 = ^-1/2 where _NR is the energy density of pressureless matter (see section 2.4) Einstein had hoped that normal matter is needed to curve the geometry; a demand, which - to him - was closely related to the Mach's principle. This hope, however, was soon shattered when de Sitter produced a solution to Einstein's equations with cosmological constant containing no matter [12]. However, in spite of two fundamental papers by Friedmann and one by Lemaitre [13, 14], most workers did not catch on with the idea of an expanding universe. In fact, Einstein originally thought Friedmann's work was in error but later published a retraction of his comment; similarly, in the Solvay meeting in 1927, Einstein was arguing against the solutions describing expanding universe. Nevertheless, the Einstein archives do contain a postcard from Einstein to Weyl in 1923 in which he says: "If there is no quasi-static world, then away with the cosmological term". The early history following de Sitter's discovery (see, for example, [15]) is clearly somewhat confused, to say the least.

It appears that the community accepted the concept of an expanding universe largely due to the work of Lemaitre. By 1931, Einstein himself had rejected the cosmological term as superflous and unjustified (see reference [16], which is a single authored paper; this paper has been mis-cited in literature often, eventually converting part of the journal name "preuss" to a co-author "Preuss, S. B"!; see [17]). There is no direct record that Einstein ever called cosmological constant his biggest blunder. It is possible that this often repeated "quote" arises from Gamow's recollection [18]: "When I was discussing cosmological problems with Einstein, he remarked that the introduction of the cosmological term was the biggest blunder he ever made in his life." By 1950's the view was decidedly against and the authors of several classic texts (like Landau and Liftshitz [7], Pauli [19] and Einstein [20]) argued against the cosmological constant.

In later years, cosmological constant had a chequered history and was often accepted or rejected for wrong or insufficient reasons. For example, the original value of the Hubble constant was nearly an order of magnitude higher [21] than the currently accepted value thereby reducing the age of the universe by a similar factor. At this stage, as well as on several later occasions (eg., [22, 23]), cosmologists have invoked cosmological constant to reconcile the age of the universe with observations (see section 3.2). Similar attempts have been made in the past when it was felt that counts of quasars peak at a given phase in the expansion of the universe [24, 25, 26]. These reasons, for the introduction of something as fundamental as cosmological constant, seem inadequate at present.

However, these attempts clearly showed that sensible cosmology can only be obtained if the energy density contributed by cosmological constant is comparable to the energy density of matter at the present epoch. This remarkable property was probably noticed first by Bondi [27] and has been discussed by McCrea [28]. It is mentioned in [1] that such coincidences were discussed in Dicke's gravity research group in the sixties; it is almost certain that this must have been noticed by several other workers in the subject.

The first cosmological model to make central use of the cosmological constantwas the steady state model [29, 30, 31]. It made use of the fact that a universe with a cosmological constant has a time translational invariance in a particular coordinate system. The model also used a scalar field with negative energy field to continuously create matter while maintaining energy conservation. While modern approaches to cosmology invokes negative energies or pressure without hesitation, steady state cosmology was discarded by most workers after the discovery of CMBR.

The discussion so far has been purely classical. The introduction of quantum theory adds a new dimension to this problem. Much of the early work [32, 33] as well as the definitive work by Pauli [34, 35] involved evaluating the sum of the zero point energies of a quantum field (with some cut-off) in order to estimate the vacuum contribution to the cosmological constant. Such an argument, however, is hopelessly naive (inspite of the fact that it is often repeated even today). In fact, Pauli himself was aware of the fact that one must exclude the zero point contribution from such a calculation. The first paper to stress this clearly and carry out a second order calculation was probably the one by Zeldovich [36] though the connection between vacuum energy density and cosmological constant had been noted earlier by Gliner [37] and even by Lemaitre [38]. Zeldovich assumed that the lowest order zero point energy should be subtracted out in quantum field theory and went on to compute the gravitational force between particles in the vacuum fluctuations. If E is an energy scale of a virtual process corresponding to a length scale l = c / E, then l^-3 = (E / c)³ particles per unit volume of energy E will lead to the gravitational self energy density of the order of

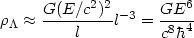(9)

This will correspond to L_P² (E / E_P)⁶ where E_P = ( c⁵ / G)^1/2 10¹⁹GeV is the Planck energy. Zeldovich took E 1 GeV (without any clear reason) and obtained a which contradicted the observational bound "only" by nine orders of magnitude.

The first serious symmetry principle which had implications for cosmological constant was supersymmetry and it was realized early on [10, 11] that the contributions to vacuum energy from fermions and bosons will cancel in a supersymmetric theory. This, however, is not of much help since supersymmetry is badly broken in nature at sufficiently high energies (at E_SS > 10² Gev). In general, one would expect the vacuum energy density to be comparable to the that corresponding to the supersymmetry braking scale, E_SS. This will, again, lead to an unacceptably large value for . In fact the situation is more complex and one has to take into account the coupling of matter sector and gravitation - which invariably leads to a supergravity theory. The description of cosmological constant in such models is more complex, though none of the attempts have provided a clear direction of attack (see e.g, [4] for a review of early attempts).

The situation becomes more complicated when the quantum field theory admits more than one ground state or even more than one local minima for the potentials. For example, the spontaneous symmetry breaking in the electro-weak theory arises from a potential of the form

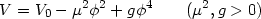(10)

At the minimum, this leads to an energy density V_min = V₀ - (µ⁴ / 4g). If we take V₀ = 0 then (V_min / g) - (300 GeV)⁴; even if g = (²) we get | V_min| ~ 10⁶ GeV⁴ which misses the bound on by a factor of 10⁵³. It is really of no help to set V_min = 0 by hand. At early epochs of the universe, the temperature dependent effective potential [39, 40] will change minimum to = 0 with V() = V₀. In other words, the ground state energy changes by several orders of magnitude during the electro-weak and other phase transitions.

Another facet is added to the discussion by the currently popular models of quantum gravity based on string theory [41, 42]. The currently accepted paradigm of string theory encompasses several ground states of the same underlying theory (in a manner which is as yet unknown). This could lead to the possibility that the final theory of quantum gravity might allow different ground states for nature and we may need an extra prescription to choose the actual state in which we live in. The different ground states can also have different values for cosmological constant and we need to invoke a separate (again, as yet unknown) principle to choose the ground state in which L_P² 10^-123 (see section 11).