


3.2. Age of the universe and cosmological constant
From equation (24) we can also determine the current age of the universe by the integral
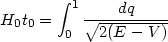 |
(34) |
Since most of the contribution to this integral comes from late times,
we can ignore the radiation term and set
 R
R
 0.
When both
0.
When both
 NR and
NR and

 are present and
are arbitrary, the age of the universe is determined by the integral
are present and
are arbitrary, the age of the universe is determined by the integral
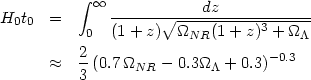 |
(35) |
The integral, which cannot be expressed in terms of elementary
functions, is well approximated by the numerical fit given in the second
line. Contours of constant H0t0
based on the (exact) integral are shown in
figure 11.
It is obvious that, for a given
 NR, the
age is higher for models with
NR, the
age is higher for models with


 0.
0.
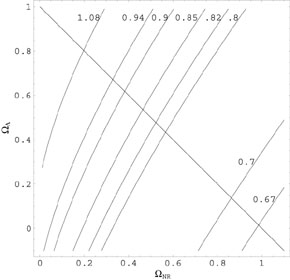 |
Figure 11. Lines of constant
H0t0 in the
|
Observationally, there is a consensus
[49,
50]
that h  0.72 ±
0.07 and
t0
0.72 ±
0.07 and
t0  13.5 ± 1.5 Gyr
[83].
This will give H0 t0 = 0.94 ± 0.14.
Comparing this result with the fit in (35), one can immediately draw
several conclusions:
13.5 ± 1.5 Gyr
[83].
This will give H0 t0 = 0.94 ± 0.14.
Comparing this result with the fit in (35), one can immediately draw
several conclusions:
 NR >
0.1, then
NR >
0.1, then

 is
non zero if H0 t0 > 0.9. A more
reasonable assumption of
is
non zero if H0 t0 > 0.9. A more
reasonable assumption of
 NR >
0.3 we will require non zero
NR >
0.3 we will require non zero

 if
H0 t0 > 0.82.
if
H0 t0 > 0.82.
 NR = 1,
NR = 1,

 = 0
and demand
t0 > 12 Gyr (which is a conservative lower bound
from stellar ages) will require h < 0.54.
Thus a purely matter dominated
= 0
and demand
t0 > 12 Gyr (which is a conservative lower bound
from stellar ages) will require h < 0.54.
Thus a purely matter dominated
 = 1 universe would
require low Hubble constant which is contradicted by
most of the observations.
= 1 universe would
require low Hubble constant which is contradicted by
most of the observations.
 NR
NR
 0.2,
0.2,

 = 0
will require H0 t0
= 0
will require H0 t0
 0.85. This still requires
ages on the lower side but values like
h
0.85. This still requires
ages on the lower side but values like
h  0.6,
t0
0.6,
t0
 13.5 Gyr
are acceptable within error bars.
13.5 Gyr
are acceptable within error bars.
 = 1 model
only if
= 1 model
only if
 NR
NR
 0.3,
0.3,


 0.7.
0.7.
If the universe is populated by dust-like matter (with w = 0) and
another component with an equation of state parameter
wX, then the age
of the universe will again be given by an integral similar to the one in
equation (35) with

 replaced by
replaced by
 X(1 +
z)3(1+wX). This will give
X(1 +
z)3(1+wX). This will give
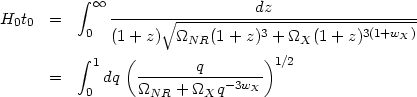 |
(36) |
The integrand varies from 0 to
( NR +
NR +
 X)-1/2 in the range of
integration for w < 0 with the rapidity of variation decided
by w. As a result, H0 t0
increases rapidly as w changes from 0 to -3 or so and then
saturates to a plateau. Even an absurdly negative value for w
like w = - 100 gives H0 t0 of
only about 1.48. This shows that even if some exotic dark energy is
present in the universe with a constant, negative w, it cannot
increase the age of the universe beyond about
H0 t0
X)-1/2 in the range of
integration for w < 0 with the rapidity of variation decided
by w. As a result, H0 t0
increases rapidly as w changes from 0 to -3 or so and then
saturates to a plateau. Even an absurdly negative value for w
like w = - 100 gives H0 t0 of
only about 1.48. This shows that even if some exotic dark energy is
present in the universe with a constant, negative w, it cannot
increase the age of the universe beyond about
H0 t0
 1.48.
1.48.
The comments made above pertain to the current age of the universe. It is also possible to obtain an expression similar to (34) for the age of the universe at any given redshift z
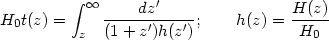 |
(37) |
and use it to constrain

 .
For example, the existence of high redshift galaxies with evolved stellar
population, high redshift radio galaxies and age dating of high redshift
QSOs can all be used in conjunction with this equation to put constrains
on
.
For example, the existence of high redshift galaxies with evolved stellar
population, high redshift radio galaxies and age dating of high redshift
QSOs can all be used in conjunction with this equation to put constrains
on 
 [84,
85,
86,
87,
88,
89].
Most of these observations require either
[84,
85,
86,
87,
88,
89].
Most of these observations require either


 0 or
0 or
 tot <
1 if they have to be consistent with
h
tot <
1 if they have to be consistent with
h  0.6.
Unfortunately, the interpretation of these observations at present requires
fairly complex modeling and hence the results are not water tight.
0.6.
Unfortunately, the interpretation of these observations at present requires
fairly complex modeling and hence the results are not water tight.