3.3. Gravitational lensing and the cosmological constant
Consider a distant source at redshift z which is lensed by some
intervening object. The lensing is most effective if the lens is located
midway between the source and the observer (see, eg., page 196 of
[46]).
This distance will be (rem/2)
if the distance to the source is rem.
(To be rigorous, one should be using angular diameter distances rather than
rem for this purpose but the essential conclusion does
not change.) To see how this
result depends on cosmology, let us consider a source
at redshift z = 2, and a lens, located optimally, in:
(a) 
= 1 matter
dominated universe, (b) a very low density matter
dominated universe in the limit of
0, (c) vacuum
dominated universe with
=
tot.
In case (a),
dH 
H-1(z)
(1 +
z)-3/2, so that
 |
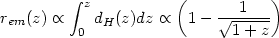(38) |
The lens redshift is determined by the equation
 |
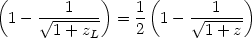(39) |
For z = 2, this gives zL = 0.608.
For case (b),
a t
giving dH
(1 +
z)-1 and rem(z)
ln(1 + z). The
equation to be solved is
(1 + zL) = (1 + z)1/2 which gives
zL = 0.732 for z = 2.
Finally, in the case of (c), dH is a constant giving
rem(z)
z and
zL = (1/2)z. Clearly, the lens redshift
is larger for vacuum dominated universe compared to the
matter dominated universe of any
.
When one considers a distribution of lenses, this will affect the
probability for lensing in a manner which depends on
.
From the observed statistics of lensing, one can put a bound on
.
More formally, one can compute the probability for
a source at redshift zs being lensed in a
+
NR = 1
universe (relative to the corresponding probability in a
NR = 1,
= 0
model). This relative probability is nearly five times larger at
zs = 1 and about thirteen
times larger for zs = 2 in a purely cosmological
constant dominated universe
[90,
91,
92,
93,
94,
2,
3].
This effect quantifies the fact that the physical
volume associated with unit redshift interval is larger in models with
cosmological constant and
hence the probability that a light ray will encounter a galaxy is larger
in these cases.
Current analysis of lensing data gives somewhat differing constraints
based on the assumptions which are made
[95,
96,
97,
98];
but typically all these constraints are about
0.7.
The result [99]
from Cosmic Lens All Sky Survey (CLASS), for example, gives
NR =
0.31+0.27-0.14 (68%)
+0.12-0.10 (systematic) for a k = 0 universe.