3.4. Other geometrical tests

The existence of a maximum for d_A(z) is a generic feature of cosmological models with _NR > 0. For a k = 0, _NR = 1 model, the maximum occurs at z_max 1.25 and z_max increases as is increased. To use this as a cosmological test, we require a class of objects with known transverse dimension and redshift. The most reliable quantity used so far corresponds to the physical wavelength acoustic vibrations in the baryon-photon gas at z 10³. This length scale is imprinted in the temperature anisotropies of the CMBR and the angular size of these anisotropies will depend on d_A and hence on the cosmological parameters; this is discussed in section 6. In principle, one could also use angular sizes of galaxies, clusters of galaxies, or radio galaxies [100, 101, 102]. Unfortunately, understanding of different physical effects and the redshift evolution of these sources make this a difficult test in practice.

There is another geometrical feature of the universe in which angular diameter distance plays an interesting role. In a closed Friedmann model with k = + 1, there is possibility that an observer at = 0 will be able to receive the light from the antipodal point = . In a purely matter dominated universe, it is easy to see that the light ray from the antipodal point = reaches = 0 exactly at the time of maximum expansion; therefore, in a closed, matter dominated universe, in the expanding phase, no observer can receive light from the antipodal point. The situation, however, is different in the presence of cosmological constant. In this case, d_A(z) (1 + z)^-1 sinµ where

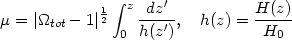(40)

It follows that d_A 0 when µ . Therefore, the angular size of an object near the antipodal point can diverge making the object extremely bright in such a universe. Assuming that this phenomena does not occur up to, say z = 6, will imply that the redshift of the antipodal point z_a(, _NR) is larger than 6. This result can be used to constrain the cosmological parameters [103, 104, 68] though the limits obtained are not as tight as some of the other tests.

Another test which can be used to obtain a handle on the geometry of the universe is usually called Alcock-Paczynski curvature test [105]. The basic idea is to use the fact that when any spherically symmetric system at high redshift is observed, the cosmological parameters enter differently in the characterization of radial and transverse dimensions. Hence any system which can be approximated a priori to be intrinsically spherical will provide a way of determining cosmological parameters. The correlation function of SDSS luminous red galaxies seems to be promising in terms of both depth and density for applying this test (see for a detailed discussion, [106, 107]). The main sources of error arises from non linear clustering and the bias of the red galaxies, either of which can be a source of systematic error. A variant of this method was proposed using observations of Lyman- forest and compare the correlation function along the line of sight and transverse to the line of sight. In addition to the modeling uncertainties, successful application of this test will also require about 30 close quasar pairs [108, 109].