Next Contents Previous

4.1. Parametrized equation of state and cosmological observations

One simple, phenomenological, procedure for comparing observations with theory is to parameterize the function w(a) in some suitable form and determine a finite set of parameters in this function using the observations. Theoretical models can then be reduced to a finite set of parameters which can be determined by this procedure. To illustrate this approach, and the difficulties in determining the equation of state of dark energy from the observations, we shall assume that w(a) is given by the simple form: w(a) = w0 + w1(1 - a); in the k = 0 model (which we shall assume for simplicity), w0 measures the current value of the parameter and - w1 gives its rate of change at the present epoch. In addition to simplicity, this parameterization has the advantage of giving finite w in the entire range 0 < a < 1.

Figure 12 shows confidence interval contours in the w0 - w1 plane arising from the full supernova data, obtained by assuming that OmegaNR + OmegaLambda = 1. The three frames are for OmegaNR = (0.2, 0.3, 0.4). The following features are obvious from the figure: (i) The cosmological constant corresponding to w0 = - 1, w1 = 0 is a viable candidate and cannot be excluded. (In fact, different analysis of many observational results lead to this conclusion consistently; in other words, at present there is no observational motivation to assume w1 neq 0.) (ii) The result is sensitive to the value of OmegaNR which is assumed. This is understandable from equation (44) which shows that wX(a) depends on both Q propto OmegaNR and H(a). (We shall discuss this dependence of the results on OmegaNR in greater detail below). (iii) Note that the axes are not in equal units in figure 12. The observations can determine w0 with far greater accuracy than w1. (iv) The slanted line again corresponds to H0dL(z = 0.63) = constant and shows that the shape of the probability ellipses arises essentially from this feature.

Figure 12

Figure 12. Confidence interval contours in the w0 - w1 plane arising from the full supernova data, for flat models with OmegaNR + OmegaLambda = 1. The three frames are for OmegaNR = (0.2, 0.3, 0.4). The data cannot rule out cosmological constant with w0 = - 1, w1 = 0. The slanted line again corresponds to H0 dL(z = 0.63) = constant and shows that the shape of the probability ellipses arises essentially from this feature.

In summary, the current data definitely supports a negative pressure component with w0 < - (1/3) but is completely consistent with w1 = 0. If this is the case, then the cosmological constant is the simplest candidate for this negative pressure component and there is very little observational motivation to study other models with varying w(a). On the other hand, the cosmological constant has well known theoretical problems which could possibly be alleviated in more sophisticated models with varying w(a). With this motivation, there has been extensive amount of work in the last few years investigating whether improvement in the observational scenario will allow us to determine whether w1 is non zero or not. (For a sample of references, see [110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125].) In the context of supernova based determination of dL, it is possible to analyze the situation along the following lines [79].

Since the supernova observations essentially measure dL(a), accuracy in the determination of w0 and w1 from (both the present and planned future [126]) supernova observations will crucially depend on how sensitive dL is to the changes in w0 and w1. A good measure of the sensitivity is provided by the two parameters

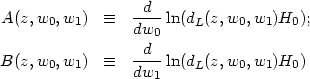Equation 45 (45)

Since dL(z, w0, w1) can be obtained from theory, the parameters A and B can be computed form theory in a straight forward manner. At any given redshift z, we can plot contours of constant A and B in the w0 - w1 plane. Figure (13) shows the result of such an analysis [79]. The two frames on the left are at z = 1 and the two frames on the right are at z = 3. The top frames give contours of constant A and bottom frame give contours of constant B. From the definition in the equation (45) it is clear that A and B can be interpreted as the fractional change in dL for unit change in w0, w1. For example, along the line marked A = 0.2 (in the top left frame) dL will change by 20 per cent for unit change in w0. It is clear from the two top frames that for most of the interesting region in the w0 - w1 plane, changing w0 by unity changes dL by about 10 per cent or more. Comparison of z = 1 and z = 3 (the two top frames) shows that the sensitivity is higher at high redshift, as to be expected. The shaded band across the picture corresponds to the region in which -1 leq w(a) leq 0 which is of primary interest in constraining dark energy with negative pressure. One concludes that determining w0 from dL fairly accurately will not be too daunting a task.

Figure 13

Figure 13. Sensitivity of dL to the parameters w0, w1. The curves correspond to constant values for the percentage of change in dLH0 for unit change in w0 (top frames), and w1 (bottom frames). Comparison of the top and bottom frames shows that dLH0 varies by few tens of percent when w0 is varied but changes by much lesser amount whenw1 is varied.

The situation, however, is quite different as regards w1 as illustrated in the bottom two frames. For the same region of the w0 - w1 plane, dL changes only by a few percent when w1 changes by unity. That is, dL is much less sensitive to w1 than to w0. It is going to be significantly more difficult to determine a value for w1 from observations of dL in the near future. Comparison of z = 1 and z = 3 again shows that the sensitivity is somewhat better at high redshifts but only marginally.

The situation is made worse by the fact that dL also depends on the parameter OmegaNR. If varying OmegaNR mimics the variation of w1 or w0, then, one also needs to determine the sensitivity of dL to OmegaNR. Figure 14 shows contours of constant H0 dL in the OmegaNR - w0 and OmegaNR - w1 planes at two redshifts z = 1 and z = 3. The two top frames shows that if one varies the value of OmegaNR in the allowed range of, say, (0.2, 0.4) one can move along the curve of constant dL and induce fairly large variation in w1. In other words, large changes in w1 can be easily compensated by small changes in OmegaNR while maintaining the same value for dL at a given redshift. This shows that the uncertainty in OmegaNR introduces further difficulties in determining w1 accurately from measurements of dL. The two lower frames show that the situation is better as regards w0. The curves are much less steep and hence varying OmegaNR does not induce large variations in w0. We are once again led to the conclusion that unambiguous determination of w1 from data will be quite difficult. This is somewhat disturbing since w1 neq 0 is a clear indication of a dark energy component which is evolving. It appears that observations may not be of great help in ruling out cosmological constant as the major dark energy component. (The results given above are based on [79]; also see [127] and references cited therein.)

Figure 14

Figure 14. Contours of constant H0dL in the OmegaNR - w0 and OmegaNR - w1 planes at two redshifts z = 1 and z = 3. The two top frames shows that a small variation of OmegaNR in the allowed range of, say, (0.2, 0.4)corresponds to fairly large variation in w1 along the curve of constant dL.

Next Contents Previous