4.2. Theoretical models with time dependent dark energy: cosmic degeneracy

The approach in the last section was purely phenomenological and one might like to construct some physical model which leads to varying w(a). It turns out that this is fairly easy, and - in fact - it is possible to construct models which will accommodate virtually any form of evolution. We shall now discuss some examples.

A simple form of the source with variable w are scalar fields with Lagrangians of different forms, of which we will discuss two possibilities:

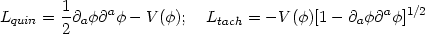(46)

Both these Lagrangians involve one arbitrary function V(). The first one, L_quin, which is a natural generalisation of the Lagrangian for a non-relativistic particle, L = (1/2) ² - V(q), is usually called quintessence (for a sample of models, see [128, 129, 130, 131, 132, 133, 134, 135, 136, 137, 138]). When it acts as a source in Friedman universe, it is characterized by a time dependent w(t) with

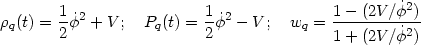(47)

The structure of the second scalar field can be understood by a simple analogy from special relativity. A relativistic particle with (one dimensional) position q(t) and mass m is described by the Lagrangian L = - m(1 - ²)^1/2. It has the energy E = m / (1 - ²)^1/2 and momentum p = m / (1 - ²)^1/2 which are related by E² = p² + m². As is well known, this allows the possibility of having massless particles with finite energy for which E² = p². This is achieved by taking the limit of m 0 and 1, while keeping the ratio in E = m / (1 - ²)^1/2 finite. The momentum acquires a life of its own, unconnected with the velocity , and the energy is expressed in terms of the momentum (rather than in terms of ) in the Hamiltonian formulation. We can now construct a field theory by upgrading q(t) to a field . Relativistic invariance now requires to depend on both space and time [ = (t, x)] and ² to be replaced by _i ⁱ . It is also possible now to treat the mass parameter m as a function of , say, V() thereby obtaining a field theoretic Lagrangian L = -V()(1 - ⁱ _i )^1/2. The Hamiltonian structure of this theory is algebraically very similar to the special relativistic example we started with. In particular, the theory allows solutions in which V 0, _i ⁱ 1 simultaneously, keeping the energy (density) finite. Such solutions will have finite momentum density (analogous to a massless particle with finite momentum p) and energy density. Since the solutions can now depend on both space and time (unlike the special relativistic example in which q depended only on time), the momentum density can be an arbitrary function of the spatial coordinate. This provides a rich gamut of possibilities in the context of cosmology. [139, 140, 141, 142, 143, 144, 145, 146, 147, 148, 149, 150, 151, 152, 153, 154, 155, 156, 157, 158, 159, 160, 161, 162, 163, 164, 165], This form of scalar field arises in string theories [166] and - for technical reasons - is called a tachyonic scalar field. (The structure of this Lagrangian is similar to those analyzed in a wide class of models called K-essence; see for example, [159]. We will not discuss K-essence models in this review.)

The stress tensor for the tachyonic scalar field can be written in a perfect fluid form

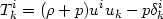(48)

with

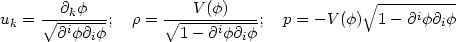(49)

The remarkable feature of this stress tensor is that it could be considered as the sum of a pressure less dust component and a cosmological constant [164] To show this explicitly, we break up the density and the pressure p and write them in a more suggestive form as

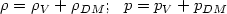(50)

where

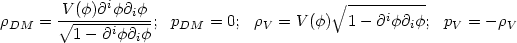(51)

This means that the stress tensor can be thought of as made up of two components - one behaving like a pressure-less fluid, while the other having a negative pressure. In the cosmological context, the tachyonic field is described by:

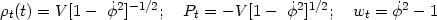(52)

When is small (compared to V in the case of quintessence or compared to unity in the case of tachyonic field), both these sources have w - 1 and mimic a cosmological constant. When >> V, the quintessence has w 1 leading to _q (1 + z)⁶; the tachyonic field, on the other hand, has w 0 for 1 and behaves like non-relativistic matter. In both the cases, -1 < w < 1, though it is possible to construct more complicated scalar field Lagrangians with even w < - 1. (See for example, [167]; for some other alternatives to scalar field models, see for example, [168].)

Since the quintessence field (or the tachyonic field) has an undetermined free function V(), it is possible to choose this function in order to produce a given H(a). To see this explicitly, let us assume that the universe has two forms of energy density with (a) = _known(a) + (a) where _known(a) arises from any known forms of source (matter, radiation, ...) and (a) is due to a scalar field. When w(a) is given, one can determine the V() using either (47) or (52). For quintessence, (47) along with (43) gives

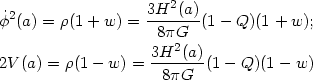(53)

For tachyonic scalar field, (52) along with (43) gives

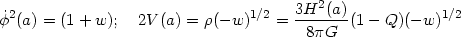(54)

Given Q(a), w(a) these equations implicitly determine V(). We have already seen that, for any cosmological evolution specified by the functions H(a) and _k(a), one can determine w(a); see equation (44). Combining (44) with either (53) or (54), one can completely solve the problem.

Let us first consider quintessence. Here, using (44) to express w in terms of H and Q, the potential is given implicitly by the form [169, 165]

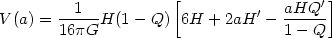	(55)
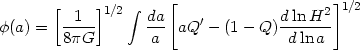	(56)

where Q(a) [8 G _known(a) / 3H²(a)]. We shall now discuss some examples of this result:

• Consider a universe in which observations suggest that H²(a) = H₀² a^-3. Such a universe could be populated by non relativistic matter with density parameter _NR = = 1. On the other hand, such a universe could be populated entirely by a scalar field with a potential V() = V₀exp[- (16 G/3)^1/2 ]. One can also have a linear combination of non relativistic matter and scalar field with the potential having a generic form V() = A exp[- B].
• Power law expansion of the universe can be generated by a quintessence model with V() = ^-. In this case, the energy density of the scalar field varies as t^{-2 / (2 + )}; if the background density _bg varies as _bg t^-2, the ratio of the two energy densities changes as ( / _bg = t^{4 / (2 + )}). Obviously, the scalar field density can dominate over the background at late times for > 0.
• A different class of models arise if the potential is taken to be exponential with, say, V() exp(- / M_Pl). When k = 0, both and _bg scale in the same manner leading to

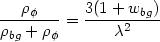  (57)

  where w_bg refers to the background parameter value. In this case, the dark energy density is said to "track" the background energy density. While this could be a model for dark matter, there are strong constraints on the total energy density of the universe at the epoch of nucleosynthesis. This requires 0.2 requiring dark energy to be sub dominant at all epochs.

• Many other forms of H(a) can be reproduced by a combination of non-relativistic matter and a suitable form of scalar field with a potential V(). As a final example [68], suppose H²(a) = H₀² [_NR a^-3 + (1 - _NR) a^-n]. This can arise, if the universe is populated with non-relativistic matter with density parameter _NR and a scalar field with the potential, determined using equations (55), (56). We get

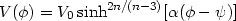  (58)

  where

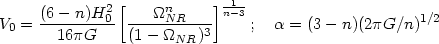  (59)

  and is a constant.

Similar results exists for the tachyonic scalar field as well [165]. For example, given any H(t), one can construct a tachyonic potential V() so that the scalar field is the source for the cosmology. The equations determining V() are now given by:

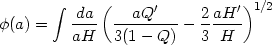	(60)
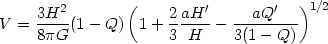	(61)

Equations (60) and (61) completely solve the problem. Given any H(t), these equations determine V(t) and (t) and thus the potential V().

As an example, consider a universe with power law expansion a = tⁿ. If it is populated only by a tachyonic scalar field, then Q = 0; further, (aH'/H) in equation (60) is a constant making a constant. The complete solution is given by

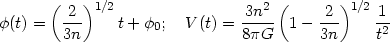(62)

where n > (2/3). Combining the two, we find the potential to be

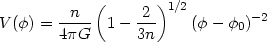(63)

For such a potential, it is possible to have arbitrarily rapid expansion with large n. (For the cosmological model, based on this potential, see [158].)

A wide variety of phenomenological models with time dependent cosmological constant have been considered in the literature. They involve power law decay of cosmological constant like t^- [170, 171, 172, 173, 174, 175, 68] or a^-, [176, 177, 178, 179, 180, 181, 182, 183, 184, 185, 186, 187, 188, 189, 190, 191], exponential decay exp(- a) [192] and more complicated models (for a summary, see [68]). Virtually all these models can be reverse engineered and mapped to a scalar field model with a suitable V(). Unfortunately, all these models lack predictive power or clear particle physics motivation.

This discussion also illustrates that even when w(a) is known, it is not possible to proceed further and determine the nature of the source. The explicit examples given above shows that there are at least two different forms of scalar field Lagrangians (corresponding to the quintessence or the tachyonic field) which could lead to the same w(a). A theoretical physicist, who would like to know which of these two scalar fields exist in the universe, may have to be content with knowing w(a). The accuracy of the determination of w(a) depends on the prior assumptions made in determining Q, as well as on the observational accuracy with which the quantities H(a) can be measured. Direct observations usually give the luminosity distance d_L or angular diameter distance d_A. To obtain H(a) from either of these, one needs to calculate a derivative [see, for example, (17)] which further limits the accuracy significantly. As we saw in the last section, this is not easy.