The conventional paradigm for the formation of structures in the
universe is based on the growth of small perturbations due to
gravitational instabilities. In this picture, some mechanism is invoked
to generate small perturbations in the energy density in the very early
phase of the universe. These perturbations grow due to gravitational
instability and eventually form the different structures which we see
today. Such a scenario can be constrained most severely by observations
of cosmic microwave background radiation (CMBR) at
z 
103. Since the perturbations in CMBR are observed to be small
(10-5 - 10-4 depending
on angular scales), it follows that the energy density perturbations
were small compared to unity at the redshift of
z 1000.
The central quantity one uses to describe
the growth of structures during 0 < z < 103 is
the density contrast defined as
(t, x) =
[
(t,
x) -
bg(t)] /
bg(t) which characterizes
the fractional change in the energy density compared to the background.
(Here bg(t) is the mean background density of
the smooth universe.) Since one is often interested in the statistical
behaviour of structures in the universe, it is conventional to assume
that
and other related
quantities are elements of an ensemble. Many popular models of structure
formation suggest that the initial density perturbations in the early
universe can be represented as a Gaussian random variable with zero mean
(that is, < > =
0) and a given initial power spectrum. The latter quantity is defined
through the relation P(t, k) = <
|k(t)|2 > where
k is
the Fourier transform of
(t, x) and
< ... > indicates averaging over the
ensemble. It is also conventional to define the two-point correlation
function 
(t,
x) as the Fourier transform of P(t, k) over
k. Though gravitational clustering will make the density contrast
non Gaussian at late times, the power spectrum and the correlation
function continue to be of primary importance in the study of structure
formation.
When the density contrast is small, its evolution can be studied by
linear perturbation theory and
each of the spatial Fourier modes k(t) will grow independently. It
follows that
(t, x)
will have the form
(t, x) =
D(t)f (x) in the linear
regime where D(t) is the growth factor and
f (x) depends on the initial configuration.
When
1, linear
perturbation theory breaks down and one needs
to either use some analytical approximation or numerical simulations to
study the non linear growth. A simple but effective approximation is
based on spherical symmetry in which one studies the dynamics of a
spherical region in the universe which has a constant over-density
compared to the background. As the universe expands, the over-dense
region will expand more slowly compared to the background, will reach a
maximum radius, contract and virialize to form a bound nonlinear system.
If the proper coordinates of the particles in a background Friedmann
universe is given by r = a(t)x we can take
the proper coordinates of the particles in the over-dense region to be
r = R(t)x where R(t) is the
expansion rate of the over-dense region. The relative acceleration of
two geodesics in the over-dense region will be
g =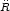 
x
= ( /
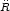R)r. Using (8) and
. r = 3,
we get
 |
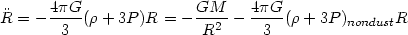(64) |
where the subscript `non-dust' refers to all components of matter other
than the one with equation of state P = 0; the dust component is
taken into account by the first term on the right hand side with
M = (4
/3)
NR
R3.
The density contrast is related to R by
(1 + ) =
( /
bg)
= (a/R)3.
Given the equation (64) satisfied by R and (20), it is easy to
determine the equation satisfied by the density contrast. We get (see
p. 404 of
[9]):
 |
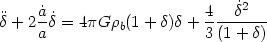(65) |
This is a fully nonlinear equation satisfied by the density contrast in a spherically symmetric over-dense region in the universe.