


5.2. Nonlinear growth of perturbations
In a purely matter dominated universe, equation (64) reduces to
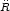 = - GM /
R2.
Solving this equation one can obtain the non linear density contrast
= - GM /
R2.
Solving this equation one can obtain the non linear density contrast
 as a function
of the redshift z:
as a function
of the redshift z:
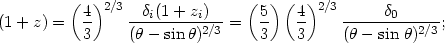 |
(82) |
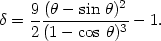 |
(83) |
Here,  0 is
the density contrast at present if the initial density contrast was
evolved by linear approximation. In general, the linear density contrast
0 is
the density contrast at present if the initial density contrast was
evolved by linear approximation. In general, the linear density contrast
 L is given by
L is given by
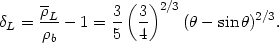 |
(84) |
When  =
(2
=
(2 /3),
/3),
 L = 0.568
and
L = 0.568
and  = 1.01
= 1.01
 1.
If we interpret
1.
If we interpret  = 1
as the transition point to nonlinearity, then such a
transition occurs at
= 1
as the transition point to nonlinearity, then such a
transition occurs at  =
(2
=
(2 /3),
/3),
 L
L
 0.57.
From (82), we see that this occurs at the redshift
(1 + znl) =
(
0.57.
From (82), we see that this occurs at the redshift
(1 + znl) =
( 0 / 0.57).
The spherical region reaches the maximum radius of expansion at
0 / 0.57).
The spherical region reaches the maximum radius of expansion at
 =
=
 .
This corresponds to a density contrast of
.
This corresponds to a density contrast of
 m
m
 4.6
which is definitely in the nonlinear regime. The linear evolution gives
4.6
which is definitely in the nonlinear regime. The linear evolution gives
 L = 1.063
at
L = 1.063
at  =
=
 .
After the spherical over dense region turns around it will continue to
contract. Equation (83) suggests that at
.
After the spherical over dense region turns around it will continue to
contract. Equation (83) suggests that at
 =
2
=
2 all the mass will collapse
to a point. A more detailed analysis of the spherical model
[199],
however, shows that
the virialized systems formed at any given time have a mean density
which is typically 200 times the background density of the universe at
that time in a
all the mass will collapse
to a point. A more detailed analysis of the spherical model
[199],
however, shows that
the virialized systems formed at any given time have a mean density
which is typically 200 times the background density of the universe at
that time in a
 NR = 1.
This occurs at a redshift of about
(1 + zcoll) =
(
NR = 1.
This occurs at a redshift of about
(1 + zcoll) =
( 0 / 1.686).
The density of the virialized structure will be approximately
0 / 1.686).
The density of the virialized structure will be approximately
 coll
coll
 170
170 0(1
+ zcoll)3 where
0(1
+ zcoll)3 where
 0 is
the present cosmological density.
The evolution is described schematically in
figure 16.
0 is
the present cosmological density.
The evolution is described schematically in
figure 16.
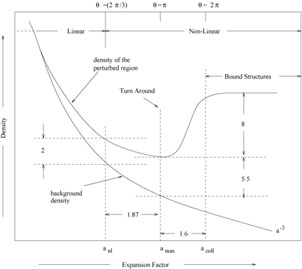 |
Figure 16. Evolution of an over dense region in spherical top-hat approximation. |
In the presence of dark energy, one cannot ignore the second term
in equation (64).
In the case of a cosmological constant, w = - 1 and
 = constant
and this extra term is independent of time. This allows one
to obtain the first integral to the equation (64) and reduce the
problem to quadrature (see, for example
[200,
201,
202]).
For a more general case of constant w with w
= constant
and this extra term is independent of time. This allows one
to obtain the first integral to the equation (64) and reduce the
problem to quadrature (see, for example
[200,
201,
202]).
For a more general case of constant w with w
 - 1, the factor
(
- 1, the factor
( + 3P)
=
+ 3P)
=  (1 + 3w)
will be time dependent because
(1 + 3w)
will be time dependent because
 will be time
dependent even for a constant w
if w
will be time
dependent even for a constant w
if w  - 1.
In this case, one cannot obtain an energy integral for the equation
(64) and the dynamics has to be determined by actual numerical
integration. Such an analysis leads to the following results
[189],
[203],
[204]:
- 1.
In this case, one cannot obtain an energy integral for the equation
(64) and the dynamics has to be determined by actual numerical
integration. Such an analysis leads to the following results
[189],
[203],
[204]:
(i) In the case of matter dominated universe, it was
found that the linear theory critical threshold for collapse,
 c, was about
1.69. This changes very little in the
presence of dark energy and an accurate fitting function
is given by
c, was about
1.69. This changes very little in the
presence of dark energy and an accurate fitting function
is given by
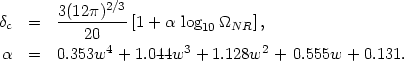 |
(85) |
(ii) The over density of a virialized structure as a function of the
redshift of virialization, however, depends more sensitively on the
dark energy component. For
-1  w
w
 - 0.3, this can be fitted
by the function
- 0.3, this can be fitted
by the function
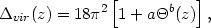 |
(86) |
where
 |
(87) |
and  (z) = 1 /
(z) = 1 /
 NR(z) - 1 = (1 /
NR(z) - 1 = (1 /
 0 - 1)(1
+ z)3w.
0 - 1)(1
+ z)3w.
The importance of
 c and
c and
 vir
arises from the fact that these quantities can be used to study the
abundance of non linear bound structures
in the universe. The basic idea behind this calculation
[205]
is as follows: Let us consider a density field
vir
arises from the fact that these quantities can be used to study the
abundance of non linear bound structures
in the universe. The basic idea behind this calculation
[205]
is as follows: Let us consider a density field
 R(x)
smoothed by a window function
WR of scale radius R. As a first approximation,
we may assume that the region with
R(x)
smoothed by a window function
WR of scale radius R. As a first approximation,
we may assume that the region with
 (R, t)
>
(R, t)
>  c (when
smoothed on the scale R at time t) will form a
gravitationally bound object with mass
M
c (when
smoothed on the scale R at time t) will form a
gravitationally bound object with mass
M 
 R3 by the time t. The
precise form of the M - R relation
depends on the window function used; for a step function
M = (4
R3 by the time t. The
precise form of the M - R relation
depends on the window function used; for a step function
M = (4 / 3)
/ 3)
 R3, while for a Gaussian
M = (2
R3, while for a Gaussian
M = (2 )3/2
)3/2
 R3. Here
R3. Here
 c is a
critical value for the density contrast given by (85). Since
c is a
critical value for the density contrast given by (85). Since
 (t) =
D(t) for the growing mode, the probability for the region
to form a bound structure at t is the same as the probability
(t) =
D(t) for the growing mode, the probability for the region
to form a bound structure at t is the same as the probability
 >
>
 c[D(ti) /
D(t)] at some early epoch ti. This
probability can be easily estimated since at sufficiently early
ti, the system is described by a Gaussian random
field. This fact can be used to calculate the number density of bound
objects leading to the result
c[D(ti) /
D(t)] at some early epoch ti. This
probability can be easily estimated since at sufficiently early
ti, the system is described by a Gaussian random
field. This fact can be used to calculate the number density of bound
objects leading to the result
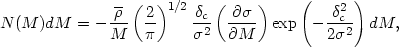 |
(88) |
The quantity  here
refers to the linearly extrapolated density contrast.
We shall now describe the constraints on dark energy arising from
structure formation.
here
refers to the linearly extrapolated density contrast.
We shall now describe the constraints on dark energy arising from
structure formation.