5.3. Structure formation and constraints on dark energy

Combining the initial power spectrum, P(k) = Akⁿ, n 1, with the transfer function in (74) we find that the final spectrum has the approximate form

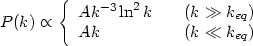(89)

with 2 k_eq^-1 d_H(z_eq) 13(_NR h²)^-1 Mpc = 13( h)^-1h^-1 Mpc [see equation (68)] where _NR h is the shape parameter (see equation (74); we have assumed _B 0 for simplicity.) From equation (89), it is clear that P(k) changes from an increasing function to a decreasing function at k_eq , the numerical value of which is decided by the shape parameter . Smaller values of _NR and will lead to more power at longer wavelengths.

One of the earliest investigations which used power spectrum to determine was based on the APM galaxy survey [206]. This work showed that the existence of large scale power requires a non zero cosmological constant. This result was confirmed when the COBE observations fixed the amplitude of the power spectrum unequivocally (see section 6). It was pointed out in [207, 208] that the COBE normalization led to a wrong shape for the power spectrum if we take _NR = 1, = 0, with more power at small scales than observed. This problem could be solved by reducing _NR and changing the shape of the power spectrum. Current observations favour 0.25. In fact, an analysis of a host of observational data, including those mentioned above suggested [209] that 0 even before the SN data came up.

Another useful constraint on the models for structure formation can be obtained from the abundance of rich clusters of galaxies with masses M 10¹⁵ M. This mass scale corresponds to a length scale of about 8h^-1 Mpc and hence the abundance of rich clusters is sensitive to the root-mean-square fluctuation in the density contrast at 8h^-1 Mpc. It is conventional to denote this quantity < ( / )² > ^1/2, evaluated at 8h^-1 Mpc, by ₈. To be consistent with the observed abundance of rich clusters, equation (88) requires ₈ 0.5_NR^-1/2. This is consistent with COBE normalization for _NR 0.3, 0.7. [Unfortunately, there is still some uncertainty about the ₈ - _NR relation. There is a claim [210] that recent analysis of SDSS data gives ₈ 0.33 ± 0.03_NR^-0.6.]

The effect of dark energy component on the growth of linear perturbations changes the value of ₈. The results of section 5.1 translate into the fitting function [189]

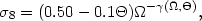(90)

where = (n - 1) + (h - 0.65) and (, ) = 0.21 - 0.22w + 0.33 + 0.25. For constant w models with w = - 1, - 2/3 and -1/3, this gives ₈ = 0.96, 0.80 and 0.46 respectively. Because of this effect, the abundance of clusters can be used to put stronger constraints on cosmology when the data for high redshift clusters improves. As mentioned before, linear perturbations grow more slowly in a universe with cosmological constant compared to the _NR = 1 universe. This means that clusters will be comparatively rare at high redshifts in a _NR = 1 universe compared to models with cosmological constant. Only less than 10 per cent of massive clusters form at z > 0.5 in a _NR = 1 universe whereas almost all massive clusters would have formed by z 0.5 in a universe with cosmological constant [211, 212, 213, 214, 75]. (A simple way of understanding this effect is by noting that if the clusters are not in place by z 0.5, say, they could not have formed by today in models with cosmological constant since there is very little growth of fluctuation between these two epochs.) Hence the evolution of cluster population as a function of redshift can be used to discriminate between these models.

An indirect way of measuring this abundance is through the lensing effect of a cluster of galaxy on extended background sources. Typically, the foreground clusters shears the light distribution of the background object and leads to giant arcs. Numerical simulations suggest [215] that a model with _NR = 0.3, = 0.7 will produce about 280 arcs which is nearly an order of magnitude larger than the number of arcs produced in a _NR = 1, = 0 model. (In fact, an open model with _NR = 0.3, = 0 will produce about 2400 arcs.) To use this effect, one needs a well defined data base of arcs and a controlled sample. At present it is not clear which model is preferred though this is one test which seems to prefer open model rather than a -CDM model.

Given the solution to (64) in the presence of dark energy, we can repeat the above analysis and obtain the abundance of different kinds of structures in the universe in the presence of dark energy. In particular this formalism can be used to study the abundance of weak gravitational lenses and virialized x-ray clusters which could act as gravitational lenses. The calculations again show [204] that the result is highly degenerate in w and _NR. If _NR is known, then the number count of weak lenses will be about a factor 2 smaller for w = - 2/3 compared to the CDM model with a cosmological constant. However, if _NR and w are allowed to vary in such a way that the matter power spectrum matches with both COBE results and abundance of x-ray clusters, then the predicted abundance of lenses is less than 25 per cent for -1 w - 0.4. It may be possible to constrain the dark energy better by comparing relative abundance of virialized lensing clusters with the abundance of x-ray under luminous lensing halos. For example, a survey covering about 50 square degrees of sky may be able to differentiate a CDM model from w = - 0.6 model at a 3 level.

Constraints on cosmological models can also arise from the modeling of damped Lyman- systems [75, 108, 109, 216, 217, 218] when the observational situation improves. At present these observations are consistent with _NR = 0.3, = 0.7 model but do not exclude other models at a high significance level.

Finally, we comment on a direct relation between (a) and H(a). Expressing equation (65) in terms of H(a) will lead to the form

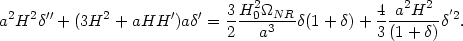(91)

This can be used to determine H²(a) from (a) since this equation is linear and first order in Q(a) H²(a) (though it is second order in ). Rewriting it in the form

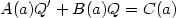(92)

where

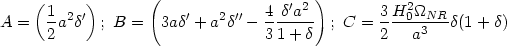(93)

We can integrate it to give the solution

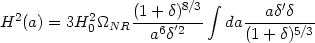(94)

This shows that, given the non linear growth of perturbations (a) as a function of redshift and the approximate validity of spherical model, one can determine H(a) and thus w(a) even during the nonlinear phases of the evolution. [A similar analysis with the linear equation (66) was done in [219], leading to the result which can be obtained by expanding (94) to linear order in .] Unfortunately, this is an impractical method from observational point of view at present.