It is possible to attack the cosmological constant problem from various other directions in which the mathematical structure of equation (3) is reinterpreted differently. Though none of these ideas have been developed into a successful formal theory, they might contain ingredients which may eventually provide a solution to this problem. Based on this hope, we shall provide a brief description of some of these ideas.
7.1. Cosmological constant as a Lagrange multiplier
The action principle for gravity in the presence of cosmological constant
 |
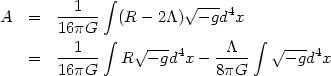(104) |
can be thought of as a variational principle extremizing the integral over R, subject to the condition that the 4-volume of the universe remains constant. To implement the constraint that the 4-volume is a constant, one will add a Lagrange multiplier term which is identical in structure to the second term in the above equation. Hence, mathematically, one can think of the cosmological constant as a Lagrange multiplier ensuring the constancy of the 4-volume of the universe when the metric is varied.
If we take this interpretation seriously, then it is necessary to
specify the 4-volume of the universe before the variation is
performed and determine the cosmological constant so that
the 4-volume has this specified volume.
A Friedmann model with positive cosmological
constant in Minkowski space will lead to a finite 3-volume
proportional to
-3/2 on
spatial integration. (To achieve this, we should use the coordinates in
which the spatial sections are closed 3-spheres.) The time integration,
however, has an arbitrary range and one needs to restrict the integration
to part of this range by invoking some physical principle.
If we take this to be typically the age of the universe, then
we will obtain a time dependent cosmological constant
(t) with
(t)
H(t)-2 remaining of order unity.
While this appears to be a conceptually attractive idea, it is not easy
to implement it in a theoretical model.
In particular, it is difficult to obtain this as a part of a generally
covariant theory incorporating gravity.