7.2. Cosmological constant as a constant of integration

Several people have suggested modifying the basic structure of general relativity so that cosmological constant will appear as constant of integration. This does not solve the problem in the sense that it still leaves its value undetermined. But this changes the perspective and allows one to think of the cosmological constant as a non dynamical entity [258, 259].

One simple way of achieving this is to assume that the determinant g of g_ab is not dynamical and admit only those variations which obeys the condition g^ab g_ab = 0 in the action principle. This is equivalent to eliminating the trace part of Einstien's equations. Instead of the standard result, we will now be led to the equation

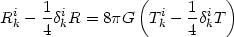(105)

which is just the traceless part of Einstien's equation. The general covariance of the action, however, implies that T^ab_;b = 0 and the Bianchi identities (Rⁱ_k - (1/2) ⁱ_k R)_;i = 0 continue to hold. These two conditions imply that _i R = - 8 G _i T requiring R + 8GT to be a constant. Calling this constant (- 4) and combining with equation (105), we get

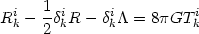(106)

which is precisely Einstien's equation in the presence of cosmological constant. In this approach, the cosmological constant has nothing to do with any term in the action or vacuum fluctuations and is merely an integration constant. Like any other integration constant its value can be fixed by invoking suitable boundary conditions for the solutions.

There are two key difficulties in this approach. The first, of course, is that it still does not give us any handle on the value of the cosmological constant and all the difficulties mentioned earlier still exists. This problem would have been somewhat less serious if the cosmological constant was strictly zero; the presence of a small positive cosmological constant makes the choice of integration constant fairly arbitrary. The second problem is in interpreting the condition that g must remain constant when the variation is performed. It is not easy to incorporate this into the logical structure of the theory. (For some attempts in this direction, see [260].)