4. GLOBALLY NEUTRAL PLASMAS

The simplified discussion of the plasma evolution is often related to magnetohydrodynamics (MHD) which is a one-fluid plasma description holding under very specific assumptions. The goal of the first part of the present Section (together with the related Appendix A) will be to present the reduction of the common two-fluids plasma dynamics to the simplified case of one-fluid description provided by MHD.

4.1. Qualitative aspects of plasma dynamics

Consider, as a starting point, a globally neutral plasma of electrons and ions (in the simplest case protons) all at the same temperature T₀ and with mean particle density n₀. Suppose, for simplicity, local thermodynamical equilibrium ⁽¹¹⁾. The charge densities will be given, respectively, by

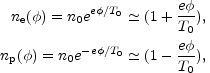(4.1)

where is the electrostatic potential. In Eqs. (4.1) it has been assumed that the plasma is weakly coupled, i.e. |e / T₀| << 1. A test charge q_t located in the origin will then experience the electrostatic potential following from the Poisson equation,

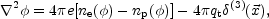(4.2)

or, using Eqs. (4.1) into Eq. (4.2)

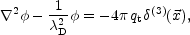(4.3)

where

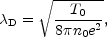(4.4)

is the Debye length. For a test particle the Coulomb potential will then have the usual Coulomb form but it will be suppressed, at large distances by a Yukawa term, i.e. e^-r/_D.

In the interstellar medium there are three kinds of regions which are conventionally defined, namely H₂ regions (where the Hydrogen is predominantly in molecular form), H⁰ regions (where Hydrogen is in atomic form) and H⁺ regions (where Hydrogen is ionized). Sometimes H⁺ regions are denoted with HI and H₂ regions with HII. In the H⁺ regions the typical temperature T₀ is of the order of 10-20 eV while for n₀ let us take, for instance, n₀ ~ 3 × 10^-2 cm^-3. Then _D ~ 30 km.

For r >> _D the Coulomb potential is screened by the global effect of the other particles in the plasma. Suppose now that particles exchange momentum through two-body interactions. Their cross section will be of the order of _em² / T₀² and the mean free path will be _mfp ~ T₀² / (_em² n₀), i.e. recalling Eq. (4.4) _D << _mfp. This means that the plasma is a weakly collisional system which is, in general, not in local thermodynamical equilibrium. This observation can be made more explicit by defining another important scale, namely the plasma frequency which, in the system under discussion, is given by

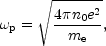(4.5)

where m_e is the electron mass. The plasma frequency is the oscillation frequency of the electrons when they are displaced from their equilibrium configuration in a background of approximately fixed ions. Recalling that v_ther (T₀ / m_e)^1/2 is the thermal velocity of the charge carriers, the collision frequency _c v_ther / _mfp is always much smaller than _p v_ther / _D. Thus, in the idealized system described so far, the following hierarchy of scales holds:

(4.6)

which means that before doing one collision the system undergoes many oscillations, or, in other words, that the mean free path is not the shortest scale in the problem. Usually one defines also the plasma parameter = n₀^-1 _D^-3, i.e. the number of particles in the Debye sphere. In the approximation of weakly coupled plasma << 1 which also imply that the mean kinetic energy of the particles is larger than the mean inter-particle potential, i.e. | e| << T₀ in the language of Eq. (4.1).