


4.2. Kinetic and fluid descriptions
From the point of view of the evolution of large-scale magnetic fields, the galaxy is globally neutral system of charged particles with typical rotation period of 3 × 108 yrs. Two complementary descriptions of the plasma can then be adopted. The first possibility is to study the full system of kinetic equations (the Vlasov-Landau description [82, 83, 84] for the one particle distribution function). In the kinetic description the "observables" of the plasma dynamics are related to the various moments of the distribution function. In a complementary perspective, it is also possible to study directly the evolution equations of the various moments of the distribution function (charge and matter densities, momentum transfer etc.). The resulting description is an effective one since not all the moments of the distribution function can be kept. The necessity of a consistent truncation in the hierarchy of the various moments is usually called closure problem. MHD is an effective description which holding for
 |
(4.7) |
where L and t are the typical length and time scales of the problem. The MHD approximation holds for typical length scales larger than the Debye scale and typical frequencies much smaller than the plasma frequency. In particular, the spectrum of plasma excitations obtained from the full kinetic description matches with the spectrum of MHD excitations but only at sufficiently small frequencies (typically of the order of the ionoacoustic waves) [85, 86].
If the plasma is weakly collisional and out of
thermodynamical equilibrium, an approximation where
the evolution equations are still tractable is given in terms of the
one-particle distribution function
fi( ,
,
 , t) where
the subscript denotes the given charge carrier (for instance
electrons and ions). The one-particle distribution obeys the
Vlasov-Landau equation for each particle species of charge
qi and of mass mi:
, t) where
the subscript denotes the given charge carrier (for instance
electrons and ions). The one-particle distribution obeys the
Vlasov-Landau equation for each particle species of charge
qi and of mass mi:
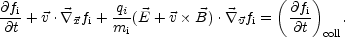 |
(4.8) |
The term appearing at the right-hand side of Eq. (4.8) is the binary collision term. In a weakly coupled plasma, the long-range force is given by the Coulomb interaction, while the short-range component arises thanks to binary collisions. In other words the electric and magnetic fields appearing in Eq. (4.8) are mean fields obeying mean Maxwell's equations:
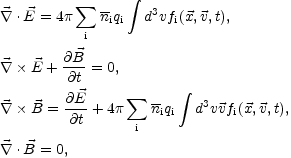 |
(4.9)
|
where  i is
the mean particle density. In the context of the kinetic approach
the evolution equation should be solved self-consistently with the
Maxwell's equations. Clearly, in a system where the density of particles
is small the mean field given by the distant particles is more
important than the the force produced by the closest particles. In
practice the Vlasov-landau system
can be linearized around some equilibrium value of the one-particle
distribution function and specific examples will be discussed later on.
i is
the mean particle density. In the context of the kinetic approach
the evolution equation should be solved self-consistently with the
Maxwell's equations. Clearly, in a system where the density of particles
is small the mean field given by the distant particles is more
important than the the force produced by the closest particles. In
practice the Vlasov-landau system
can be linearized around some equilibrium value of the one-particle
distribution function and specific examples will be discussed later on.
The one-particle distribution function is not directly observable. The directly observable quantities are the the various moments of the one-particle distribution, for instance, the particle density,
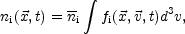 |
(4.13) |
and the related matter and charge densities for each particle
species (i.e.  m,i(
m,i( , t) = mi
ni(
, t) = mi
ni( , t) and
, t) and
 q,i(
q,i( , t) = qi
ni(
, t) = qi
ni( , t)) or summed over the different species (i.e.
, t)) or summed over the different species (i.e.
 m
=
m
=  i
i
 m,i and
m,i and
 q =
q =
 i
i
 q,i).
However, the dynamical informations on the plasma evolution are not only
encoded in the moment of order zero but also in the higher moments (the
first, the second and even higher).
q,i).
However, the dynamical informations on the plasma evolution are not only
encoded in the moment of order zero but also in the higher moments (the
first, the second and even higher).
For some class of problems the kinetic approach is to be preferred. For instance the kinetic approach is mandatory for all the high frequency phenomena (like, for instance, equilibration of charge and current density fluctuations). As far as the low-frequency phenomena are concerned one can imagine to obtain a reduced (fluid-like) description.