4.3. From one-fluid equations to MHD

The evolution equations for the one-fluid variables are obtained from the two-species kinetic description by some algebra which is summarized in the first part of Appendix A. The bottom line of the derivation is that the moments of the one-particle distribution function obey a set of partial differential equations whose solutions can be studied in different approximations. One of these approximations is the MHD description. The set of one-fluid equations (derived in Appendix A) can be written as

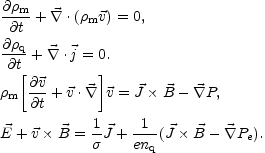(4.14) (4.15) (4.16) (4.17)

supplemented by the Maxwell's equations

(4.18) (4.19) (4.20)

Eqs. (4.14) and (4.15) are the mass and charge conservation, Eq. (4.16) is the equation for the momentum transfer and Eq. (4.17) is the generalized Ohm law. In Eqs. (4.14)-(4.17) is the one-fluid velocity field, P is the total pressure and P_e is the pressure of the electrons.

If the plasma is globally neutral the charge density can be consistently neglected. However, global neutrality is plausible only for typical lengths much larger than _D where the collective properties of the plasma are the leading dynamical effect. Under this assumption, Eqs. (4.15) and (4.18) imply

(4.21)

which means that MHD currents are, in the first approximation, solenoidal.

The second step to get to a generalized form of the MHD equations is to neglect the terms responsible for the high frequency plasma excitations, like the displacement current in Eqs. (4.20) whose form becomes then

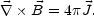(4.22)

Given the two sets of consistent approximations discussed so far, the form taken by the generalized Ohm law may not be unique and, therefore, different MHD descriptions arise depending upon which term at the right hand side of Eq. (4.17) is consistently neglected. The simplest (but often not realistic) approximation is to neglect all the terms at the right hand side of Eq. (4.17). This is sometimes called ideal MHD approximation. In this case the Ohmic electric field is given by - × . 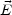This ideal description is also called sometimes superconducting MHD approximation since, in this case, the resistive terms in Eq. (4.17), i.e. 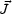/ go to zero (and the conductivity ). In the early Universe it is practical to adopt the superconducting approximation (owing to the large value of the conductivity) but it is also very dangerous since all the (1 / ) effects are dropped.

A more controllable approximation is the real (or resistive) MHD. The resistive approximation is more controllable since the small expansion parameter (i.e. 1 / ) is not zero (like in the ideal case) but it is small and finite. This allows to compute the various quantities to a a given order in 1 / even if, for practical purposes, only the first correction is kept. In this framework the Ohmic current is not neglected and the generalized Ohm law takes the form

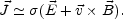(4.23)

Comparing Eq. (4.23) with Eq. (4.17), it is possible to argue that the resistive MHD scheme is inadequate whenever the Hall and thermoelectric terms are cannot be neglected. Defining _B = eB / m as the Larmor frequency, the Hall term 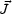× can be neglected provided L _p² / _B v₀ >> 1 where L us the typical size of the system and v₀ the typical bulk velocity of the plasma. With analogous dimensional arguments it can be argued that the pressure gradient, i.e. the thermoelectric term, can be consistently neglected provided Lv_{0 B} m_e / T_e >> 1. Specific examples where the Hall term may become relevant will be discussed in the context of the Biermann battery mechanism.

The set of MHD equations, as it has been presented so far, is not closed if a further relation among the different variables is not specified [87]. Typically this is specified through an equation relating pressure and matter density (adiabatic or isothermal closures). Also the incompressible closure (i.e. ^. = 0) is often justified in the context of the evolution of magnetic fields prior to recombination. It should be stressed that sometimes the adiabatic approximation may lead to paradoxes. It would correspond, in the context of ideal MHD, to infinite electrical conductivity and vanishingly small thermal conductivity (i.e. the electrons should be extremely fast not to feel the resistivity and, at the same time, extremely slow not to exchange heat among them).