


4.4. The Alfvén theorems
The ideal and resistive MHD descriptions are rather useful in order to illustrate some global properties of the evolution of the plasma which are relevant both in the evolution of large-scale magnetic fields prior to recombination and in the discussion of the gravitational collapse in the presence of magnetic fields. These global properties of the plasma evolution go under the name of Alfvén theorems [87] (see also [88]).
In the ideal limit both the magnetic flux and the magnetic helicity are conserved. This means,
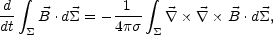 |
(4.24) |
where  is an
arbitrary closed surface which moves with the
plasma (12).
If
is an
arbitrary closed surface which moves with the
plasma (12).
If 

 the expression
appearing at the right hand side is sub-leading
and the magnetic flux lines evolve glued to the plasma element.
the expression
appearing at the right hand side is sub-leading
and the magnetic flux lines evolve glued to the plasma element.
The other quantity which is conserved in the superconducting limit is the magnetic helicity
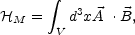 |
(4.25) |
where 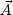 is the
vector potential whose presence may lead to think that the
whole expression (4.25) is not gauge-invariant. In fact
is the
vector potential whose presence may lead to think that the
whole expression (4.25) is not gauge-invariant. In fact
 .
.
 is not gauge
invariant but, none the less,
is not gauge
invariant but, none the less,
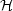 M is
gauge-invariant since
the integration volume is defined in such a way that the magnetic field
M is
gauge-invariant since
the integration volume is defined in such a way that the magnetic field
 is parallel to the surface which bounds V and which we will call
is parallel to the surface which bounds V and which we will call
 V. If
V. If
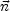 is the unit
vector normal to
is the unit
vector normal to
 V
then
V
then  .
.
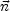 = 0 on
= 0 on
 V and the
gauge dependent
contribution to the integral appearing in Eq. (4.25) vanishes.
In physical terms the integration may always be performed imagining
that the space is sliced in flux tubes of the magnetic field. This
procedure is correct provided the magnetic flux is, at least
approximately, conserved as implied by Eq. (4.24).
V and the
gauge dependent
contribution to the integral appearing in Eq. (4.25) vanishes.
In physical terms the integration may always be performed imagining
that the space is sliced in flux tubes of the magnetic field. This
procedure is correct provided the magnetic flux is, at least
approximately, conserved as implied by Eq. (4.24).
The magnetic gyrotropy
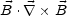 |
(4.26) |
it is a gauge invariant measure of the diffusion rate of
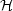 M. In
fact, in the resistive approximation
[88]
M. In
fact, in the resistive approximation
[88]
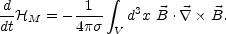 |
(4.27) |
As in the case of Eq. (4.25), for


 the magnetic helicity
is approximately constant.
The value of the magnetic gyrotropy allows to distinguish
different mechanisms for the magnetic field generation. Some
mechanisms are able to produce magnetic fields whose
flux lines have a non-trivial gyrotropy.
The properties of turbulent magnetized plasmas may change
depending upon the value of the gyrotropy and of the helicity
[87].
the magnetic helicity
is approximately constant.
The value of the magnetic gyrotropy allows to distinguish
different mechanisms for the magnetic field generation. Some
mechanisms are able to produce magnetic fields whose
flux lines have a non-trivial gyrotropy.
The properties of turbulent magnetized plasmas may change
depending upon the value of the gyrotropy and of the helicity
[87].
The physical interpretation of the flux and magnetic
helicity conservation is the following. In MHD the magnetic field
has to be always solenoidal (i.e.
 .
.  = 0).
Thus, the magnetic flux conservation implies that, in the
superconducting limit (i.e.
= 0).
Thus, the magnetic flux conservation implies that, in the
superconducting limit (i.e. 

 ) the
magnetic flux lines, closed because of the transverse nature of the
field, evolve always glued together with the plasma element. In this
approximation, as far as the magnetic field
evolution is concerned, the plasma is a collection
of (closed) flux tubes. The theorem of flux conservation
states then that the energetical properties of large-scale
magnetic fields are conserved throughout the plasma evolution.
) the
magnetic flux lines, closed because of the transverse nature of the
field, evolve always glued together with the plasma element. In this
approximation, as far as the magnetic field
evolution is concerned, the plasma is a collection
of (closed) flux tubes. The theorem of flux conservation
states then that the energetical properties of large-scale
magnetic fields are conserved throughout the plasma evolution.
While the flux conservation concerns the energetical properties of the magnetic flux lines, the magnetic helicity concerns chiefly the topological properties of the magnetic flux lines. If the magnetic field is completely stochastic, the magnetic flux lines will be closed loops evolving independently in the plasma and the helicity will vanish. There could be, however, more complicated topological situations [88] where a single magnetic loop is twisted (like some kind of Möbius stripe) or the case where the magnetic loops are connected like the rings of a chain. In both cases the magnetic helicity will not be zero since it measures, essentially, the number of links and twists in the magnetic flux lines. Furthermore, in the superconducting limit, the helicity will not change throughout the time evolution. The conservation of the magnetic flux and of the magnetic helicity is a consequence of the fact that, in ideal MHD, the Ohmic electric field is always orthogonal both to the bulk velocity field and to the magnetic field. In the resistive MHD approximation this is no longer true.
If the conductivity is very large (but finite), the resistive MHD approximation suggests, on one hand, that the magnetic flux is only approximately conserved. On the other hand the approximate conservation of the magnetic helicity implies that the closed magnetic loops may modify their topological structure. The breaking of the flux lines, occurring at finite conductivity, is related to the possibility that bits of magnetic fluxes are ejected from a galaxy into the inter-galactic medium. This phenomenon is called magnetic reconnection and it is the basic mechanism explaining, at least qualitatively, why, during the solar flares, not only charged particles are emitted, but also magnetic fields. In the context of large scale magnetic fields the approximate (or exact) magnetic flux conservation has relevant consequences for the rôle of magnetic fields during gravitational collapse.
12 Notice that in Ref.
[88]
Eq. (4.24) has been derived without the
4 term at the right hand side
because of different conventions.
Back.
term at the right hand side
because of different conventions.
Back.