


5.4. Charge and current density fluctuations
As a simple application of kinetic techniques, it is useful to understand which magnetic field can be obtained from an initial inhomogeneous distribution of charge and current density fluctuations.
Consider then the system of Eqs. (5.38) under the assumption that, initially, electric and magnetic fields vanish:
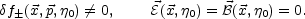 |
(5.68) |
Using Eqs. (5.36)-(5.38) the induced magnetic fields can be obtained.. This problem is discussed, in greater detail, in [134].
Subtracting Eqs. (5.36) and (5.37), and defining
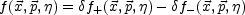 |
(5.69) |
the Vlasov-Landau system can be written as
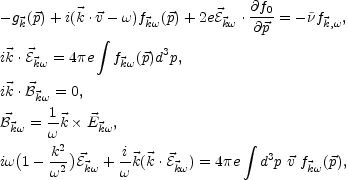 |
(5.70) (5.71) (5.72) (5.73) (5.74) |
where g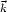 (
(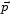 ) is the initial profile of the
distribution function and where
) is the initial profile of the
distribution function and where
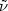 is the typical
collision frequency. The subscripts
is the typical
collision frequency. The subscripts
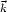
 denote the Fourier
transform with respect to space and the Laplace transform with respect
to time of the corresponding quantity.
denote the Fourier
transform with respect to space and the Laplace transform with respect
to time of the corresponding quantity.
After enforcing the Gauss constraint at the initial time, the electric field can be separated in its polarizations parallel and transverse to the direction of propagation of the fluctuation. The transverse current provides a source for the evolution of transverse electric field fluctuations
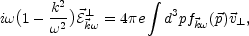 |
(5.75) |
whereas the charge fluctuations provide a source for the evolution of longitudinal electric field fluctuations
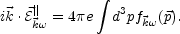 |
(5.76) |
In Eqs. (5.75) and (5.76) the longitudinal and transverse part of the electric field fluctuations have been defined:
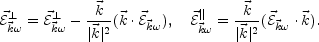 |
(5.77) |
The solution of Eq. (5.70) is given by
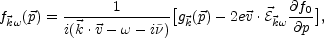 |
(5.78) |
where we used that
 f0
/
f0
/ 
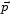


 f0
/
f0
/  p.
The longitudinal and transverse components of the electric
fluctuations can be obtained by inserting Eq. (5.78) into Eqs.
(5.75)-(5.76)
p.
The longitudinal and transverse components of the electric
fluctuations can be obtained by inserting Eq. (5.78) into Eqs.
(5.75)-(5.76)
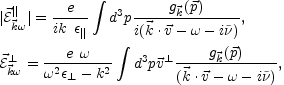 |
(5.79)
|
where  ||
and
||
and 
 are,
respectively, the longitudinal and transverse part of the
polarization tensor
are,
respectively, the longitudinal and transverse part of the
polarization tensor
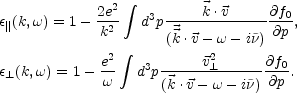 |
(5.81)
|
Now, the general expression for the generated magnetic field is
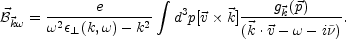 |
(5.83) |
The space-time evolution of the magnetic fluctuations can be determined by performing the inverse Laplace and Fourier transforms:
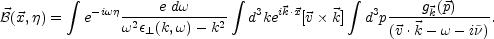 |
(5.84) |
In order to perform this integral, the explicit relations for the polarization tensors should be given. They depend on the equilibrium distribution function f0(p), which we take to be the expression given in Eq. (5.34) (21)
Then we have for transverse polarization
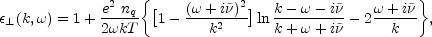 |
(5.85) |
and for the longitudinal polarization:
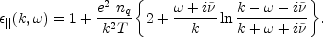 |
(5.86) |
Consider now the case of very small momenta
k <<  and
and
 <<
<<
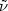 , relevant for
long-ranged magnetic fields. Then the
computation of the integral (5.84) in the large time limit and with
the use of explicit form of the transverse polarization tensor in
(5.85) gives (22):
, relevant for
long-ranged magnetic fields. Then the
computation of the integral (5.84) in the large time limit and with
the use of explicit form of the transverse polarization tensor in
(5.85) gives (22):
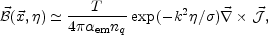 |
(5.87) |
where  is the plasma
conductivity in the relaxation time approximation,
is the plasma
conductivity in the relaxation time approximation,
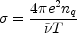 |
(5.88) |
and initial electric current is given by
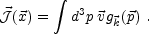 |
(5.89) |
The obtained results assumed that the linearization of the Vlasov equation is consistent with the physical assumptions of our problem. This is indeed the case. In order to safely linearize the Vlasov equation we have to make sure that the perturbed distribution function of the charge fluctuations is always smaller than the first order of the perturbative expansion (given by the distribution of Eq. 5.34). In other words we have to make sure that
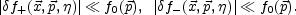 |
(5.90) |
These conditions imply that
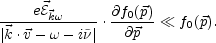 |
(5.91) |
If the relativistic plasma frequency is defined,
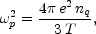 |
(5.92) |
the condition expressed by Eq. (5.91) can be restated, for modes
k 
 p, as
|
p, as
|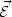
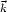 ,
, |2 <
nqT (where we essentially took the
square modulus of Eq. (5.91)). This last inequality expresses
the fact that the energy density associated with the gauge field
fluctuations should always be smaller than the critical energy
density stored in radiation. The linear treatment of the Vlasov
equation is certainly accurate provided the typical modes of the the
field are smaller than the plasma frequency and provided the energy
density in electric and magnetic fields is smaller than
T4, i.e. the energy density stored in the radiation
background.
|2 <
nqT (where we essentially took the
square modulus of Eq. (5.91)). This last inequality expresses
the fact that the energy density associated with the gauge field
fluctuations should always be smaller than the critical energy
density stored in radiation. The linear treatment of the Vlasov
equation is certainly accurate provided the typical modes of the the
field are smaller than the plasma frequency and provided the energy
density in electric and magnetic fields is smaller than
T4, i.e. the energy density stored in the radiation
background.
21 Notice that most of our considerations can be easily extended to the case of a Bose-Einstein or Fermi-Dirac distribution. What is important, in our context, is the analytical structure of the polarization tensors and this is the same for different distributions [125]. Back.
22 For small k, the equation
 2
2

 (k,
(k,
 ) - k2
= 0 defining the poles of the inverse Laplace transform implies
) - k2
= 0 defining the poles of the inverse Laplace transform implies
 ~ i k2 /
~ i k2 /
 .
Back.
.
Back.