


5.6. Hypermagnetic fields
At small temperatures and small densities of the different
fermionic charges the SUL(2)
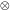 UY(1) is broken down to the
Uem(1) and the long range fields which can
survive in the plasma are the ordinary magnetic fields.
For sufficiently high temperatures
(and for sufficiently high values of the various fermionic charges) the
SUL(2)
UY(1) is broken down to the
Uem(1) and the long range fields which can
survive in the plasma are the ordinary magnetic fields.
For sufficiently high temperatures
(and for sufficiently high values of the various fermionic charges) the
SUL(2)
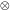 UY(1) is restored and
non-screened vector modes correspond to hypermagnetic fields.
In fact, Abelian electric fields decay within a typical time scale
1/
UY(1) is restored and
non-screened vector modes correspond to hypermagnetic fields.
In fact, Abelian electric fields decay within a typical time scale
1/ where
where
 is the conductivity.
The long-ranged non-Abelian magnetic fields (corresponding, for instance,
to the color SU(3) or to the weak SU(2)) cannot exist
because at high temperatures the non-Abelian interactions
induce a "magnetic" mass gap ~ g2T where
g is the gauge coupling constant.
Also the non-Abelian electric fields decay because of the finite value
of the conductivity as it occurs for Abelian electric fields.
Therefore, the only long scale field that can
exist in the plasma for enough time must be associated with some
Abelian U(1) group. This statement, valid to all orders in
perturbation theory, has been confirmed non-perturbatively for the
electroweak theory by recent lattice studies in
[165].
Under normal conditions (i.e.
small temperatures and small densities of the different fermionic
charges) the SU(2)×U(1)Y symmetry is "broken" down to
U(1)EM, the massless field corresponding to U(1)EM
is the ordinary photon and the only long-lived field in the
plasma is the ordinary magnetic one. At sufficiently high
temperatures, T > Tc, the
SU(2)×U(1)Y symmetry is
"restored", and non-screened vector modes Yµ
correspond to the U(1)Y hypercharge group. Hence, if
primordial fields existed at T > Tc, they
did correspond to hypercharge rather than to U(1)EM.
is the conductivity.
The long-ranged non-Abelian magnetic fields (corresponding, for instance,
to the color SU(3) or to the weak SU(2)) cannot exist
because at high temperatures the non-Abelian interactions
induce a "magnetic" mass gap ~ g2T where
g is the gauge coupling constant.
Also the non-Abelian electric fields decay because of the finite value
of the conductivity as it occurs for Abelian electric fields.
Therefore, the only long scale field that can
exist in the plasma for enough time must be associated with some
Abelian U(1) group. This statement, valid to all orders in
perturbation theory, has been confirmed non-perturbatively for the
electroweak theory by recent lattice studies in
[165].
Under normal conditions (i.e.
small temperatures and small densities of the different fermionic
charges) the SU(2)×U(1)Y symmetry is "broken" down to
U(1)EM, the massless field corresponding to U(1)EM
is the ordinary photon and the only long-lived field in the
plasma is the ordinary magnetic one. At sufficiently high
temperatures, T > Tc, the
SU(2)×U(1)Y symmetry is
"restored", and non-screened vector modes Yµ
correspond to the U(1)Y hypercharge group. Hence, if
primordial fields existed at T > Tc, they
did correspond to hypercharge rather than to U(1)EM.
At the electroweak epoch the typical size of the Hubble radius is of the order of 3 cm . The typical diffusion scale is of the order of 10-9 cm. Therefore, over roughly eight orders of magnitude hypermagnetic fields can be present in the plasma without being dissipated [163].
5.6.1. Anomalous MHD equations
The evolution of hypermagnetic fields can be obtained from the anomalous magnetohydrodynamical (AMHD) equations. The AMHD equations generalize the treatment of plasma effects involving hypermagnetic fields to the case of finite fermionic density [164].
There are essential differences between the interactions of magnetic
fields and the ones of hypermagnetic fields with matter. The ordinary
electromagnetic field has a vector-like coupling to the fermions, while
the coupling of the hypercharge fields is chiral. Thus, if hyperelectric
(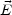 Y)
and hypermagnetic
(
Y)
and hypermagnetic
(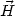 Y)
fields are present
simultaneously, they cause a variation of the fermionic number
according to the anomaly equation,
Y)
fields are present
simultaneously, they cause a variation of the fermionic number
according to the anomaly equation,
 µ
jµ ~ g'2 / (4
µ
jµ ~ g'2 / (4
 2)
2)
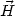 Y
.
Y
.
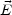 Y (here
g' the hypercharge gauge coupling constant). Now, the presence of
non-homogeneous hypermagnetic fields in the EW plasma with
(hyper)conductivity
Y (here
g' the hypercharge gauge coupling constant). Now, the presence of
non-homogeneous hypermagnetic fields in the EW plasma with
(hyper)conductivity
 c always
implies the existence of a related electric field,
c always
implies the existence of a related electric field,
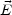 Y ~
1 /
Y ~
1 /  c
c
 ×
×
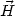 Y.
Since for a general stochastic magnetic background
<(
Y.
Since for a general stochastic magnetic background
<(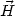 Y
.
Y
.
 ×
×
 Y)2>
Y)2>
 0, the non-uniform
hypermagnetic field may absorb or release fermions and produce, ultimately,
baryon and lepton density perturbations because of the anomaly equation.
0, the non-uniform
hypermagnetic field may absorb or release fermions and produce, ultimately,
baryon and lepton density perturbations because of the anomaly equation.
The behaviour of cold fermionic matter with non-zero anomalous Abelian charges was considered in [166] where it was pointed out that the anomalous fermionic matter is unstable against the creation of Abelian gauge field with non-zero Chern-Simons number, which eats up fermions because of the anomaly. The right electron number density may be converted to the hypercharge field because of a similar effect. Also the opposite effect is possible: hypercharge fields may be converted into fermions in a hot environment.
The electroweak plasma in complete thermal equilibrium at a temperature T can be characterized by nf chemical potentials µi, i = 1,..., nf corresponding to the exactly conserved global charges
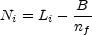 |
(5.105) |
(Li is the lepton number of the i-th generation, B is the baryon number, and nf is the number of fermionic generations). One should also introduce a chemical potential µY corresponding to weak hypercharge, but its value is fixed from the requirement of the hypercharge neutrality of the plasma, <Y> = 0.
It is interesting to study this plasma slightly out of thermal equilibrium, for instance in the situation where a non-uniform distribution of the hypermagnetic field is present. Because of the anomaly, this field is coupled to the fermionic number densities. In principle, different chemical potentials can be assigned to all the fermionic degrees of freedom of the electroweak theory (45 if nf = 3) and the coupled system of Boltzmann-type equations for these chemical potentials and the hypercharge fields may be written. Since we are interested in the slow processes in the plasma, this is not necessary. If the coupling, corresponding to some slow process, is switched off, then the electroweak theory acquires an extra conserved charge and a further chemical potential should be added to the system given in Eq. (5.105).
An interesting observation (which turns out to be quite important in our context) has been made in [167, 168, 169], where it was noticed that perturbative reactions with right-handed electron chirality flip are out of thermal equilibrium at temperatures higher than some temperature TR. (23) Thus, the number of right electrons is perturbatively conserved at temperatures T > TR and the chemical potential µR can be introduced for it. On the other hand, this charge is not conserved because of the Abelian anomaly,
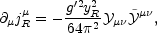 |
(5.106) |
and it is therefore coupled to the hypermagnetic field.
Here 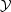 and
and
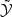 are, respectively, the UY(1) hypercharge field
strengths and their duals, g' is the associated gauge coupling
and yR = -2 is the hypercharge of the right electron.
are, respectively, the UY(1) hypercharge field
strengths and their duals, g' is the associated gauge coupling
and yR = -2 is the hypercharge of the right electron.
Now we are ready to derive the anomalous MHD equations in flat space [163, 164]. The effective Lagrangian density describing the dynamics of the gauge fields at finite fermionic density is [170]:
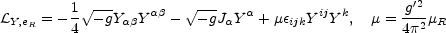 |
(5.107) |
(g is the determinant of the metric defined in (5.1);
Y
 =
=
 [
[ Y
Y ];
];

 is the covariant
derivative with respect to the metric (5.1) [notice that in the
metric (5.1)
is the covariant
derivative with respect to the metric (5.1) [notice that in the
metric (5.1)  [
[ Y
Y ] =
] =
 [
[ Y
Y ]]; g' is the Abelian coupling constant).
The first and the last terms in Eq. (5.107) are nothing but the
curved space generalization of the flat-space effective Lagrangian for
the hypercharge fields at finite fermion density
[163,
164],
J
]]; g' is the Abelian coupling constant).
The first and the last terms in Eq. (5.107) are nothing but the
curved space generalization of the flat-space effective Lagrangian for
the hypercharge fields at finite fermion density
[163,
164],
J is
the ohmic current. The equations of motion for the
hyperelectric and hypermagnetic fields are then
is
the ohmic current. The equations of motion for the
hyperelectric and hypermagnetic fields are then
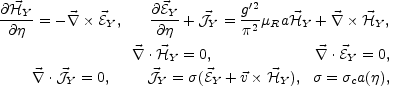 |
(5.108) |
with the same notations introduced in the case of the conventional MHD equations.
To Eqs. (5.108), the evolution equation of the right electron chemical potential, accounting for the anomalous and perturbative non-conservation of the right electron number density (nR), must be added:
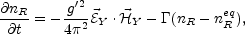 |
(5.109) |
where  is the
perturbative chirality-changing rate,
is the
perturbative chirality-changing rate,
 = T
TR / M0,
nReq is
the equilibrium value of the right electron number density,
and the term proportional to
= T
TR / M0,
nReq is
the equilibrium value of the right electron number density,
and the term proportional to
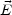 Y
.
Y
.
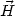 Y is
the right electron anomaly contribution.
Y is
the right electron anomaly contribution.
Finally, the relationship between the right electron number density and the chemical potential must be specified. This relation depends upon the particle content of the theory. In the case of the Minimal Standard Models (MSM) the evolution equation of the chemical potential becomes [164]
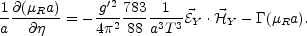 |
(5.110) |
At finite hyperconductivity (in what we would call, in a MHD context, resistive approximation) we have that from Eq. (5.108) the induced hyperelectric field is not exactly orthogonal to the hypermagnetic one and, moreover, an extra "fermionic" current comes in the game thanks to the fact that we are working at finite chemical potential. Therefore in our context the resistive Ohm law can be written as
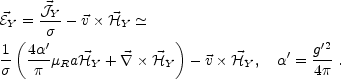 |
(5.111) |
In the bracket appearing in
Eq. (5.111) we can identify two different contributions. One is
associated with the curl of the magnetic field. We will call this the MHD
contribution, since it appears in the same way in ordinary plasmas.
The other contribution contains the chemical potential and it is
directly proportional to the magnetic field and to the chemical
potential. This is a typical finite density effect. In fact the extra
Ohmic current simply describes the possibility that the energy sitting
in real fermionic degrees of freedom can be transferred to the
hypermagnetic field. It may be of some interest to
notice the analogy between the first term of Eq. (5.111) and the
typical form of the ohmic current discussed in Eq. (4.17)
appearing in the context of the dynamo mechanism. In the latter case the
presence of a current (proportional to the vorticity through the
 dynamo term) was
indicating that large length scales
magnetic fields could grow by eating up fluid vortices. By inserting
dynamo term) was
indicating that large length scales
magnetic fields could grow by eating up fluid vortices. By inserting
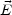 Y
obtained from the generalized Ohm law
(5.111) in the evolution equations (5.108) of the
hypercharge fields, we obtain the generalized form of the magnetic
diffusivity equation:
Y
obtained from the generalized Ohm law
(5.111) in the evolution equations (5.108) of the
hypercharge fields, we obtain the generalized form of the magnetic
diffusivity equation:
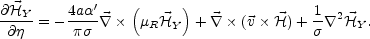 |
(5.112) |
In order to be consistent with our resistive approach we neglected terms
containing time derivatives of the electric field, which are
sub-leading provided the conductivity is finite. In our considerations
we will also make a further simplification, namely we will assume
that the EW plasma is (globally) parity-invariant and that,
therefore, no global vorticity is present. Therefore, since the
length scale of variation of the bulk velocity field is much shorter
than the correlation distance of the hypermagnetic field, the
infrared modes of the hypercharge will be practically unaffected by
the velocity of the plasma, which will be neglected when the large-scale
part of the hypercharge is concerned. This corresponds to the usual MHD
treatment of a mirror symmetric plasma (see, e.g. Eq. (4.32)-(4.34), when
 = 0).
= 0).
Eqs. (5.112) and (5.110) form a set of AMHD equations for the hypercharge magnetic field and right electron chemical potential in the expanding Universe.
The Abelian nature of the hypercharge field does not forbid that the hypermagnetic flux lines should have a trivial topological structure. This situation is similar to what already encountered in the case of conventional electromagnetic fields with the important difference that the evolution equations of hypermagnetic fields are different from the ones of ordinary magnetic fields. After a swift summary of the properties of hypermagnetic knots (based on [171, 172]), some interesting applications of these hypercharge profiles will be reviewed.
In the gauge Y0 = 0,
 .
. = 0,
an example of topologically non-trivial configuration of the hypercharge
field is the Chern-Simons wave
[173,
174,
175]
= 0,
an example of topologically non-trivial configuration of the hypercharge
field is the Chern-Simons wave
[173,
174,
175]
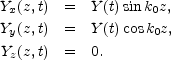 |
(5.113) |
This particular configuration is not homogeneous but it describes a hypermagnetic knot with homogeneous helicity and Chern-Simons number density
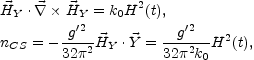 |
(5.114) |
where 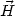 Y =
Y =
 ×
×
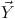 ,
H(t) = k0 Y(t); g'
is the U(1)Y coupling.
,
H(t) = k0 Y(t); g'
is the U(1)Y coupling.
It is possible to construct hypermagnetic knot configurations with finite energy and helicity which are localized in space and within typical distance scale Ls. Let us consider in fact the following configuration in spherical coordinates [172]
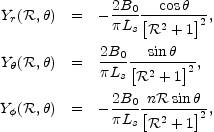 |
(5.115) |
where  = r /
Ls is the rescaled radius and B0 is
some dimensionless amplitude and n is just an integer number
whose physical interpretation will become clear in a moment.
The hypermagnetic field can be easily computed
from the previous expression and it is
= r /
Ls is the rescaled radius and B0 is
some dimensionless amplitude and n is just an integer number
whose physical interpretation will become clear in a moment.
The hypermagnetic field can be easily computed
from the previous expression and it is
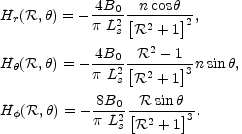 |
(5.116) |
The poloidal and toroidal components of
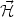 can be usefully
expressed as
can be usefully
expressed as
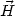 p =
Hr
p =
Hr
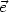 r +
H
r +
H
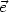
 and
and
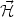 t =
t =
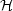

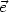
 .
The Chern-Simons number is finite and it is given by
.
The Chern-Simons number is finite and it is given by
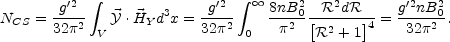 |
(5.117) |
The total helicity of the configuration can also be computed
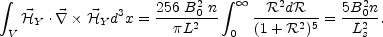 |
(5.118) |
We can compute also the total energy of the field
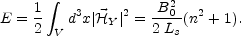 |
(5.119) |
and we discover that it is proportional to n2. This means that one way of increasing the total energy of the field is to increase the number of knots and twists in the flux lines.
This type of configurations can be also obtained by projecting a non-Abelian SU(2) (vacuum) gauge field on a fixed electromagnetic direction [176] (24). The resulting profile of the knot depends upon an arbitrary function of the radial distance.
These configurations have been also studied in [178, 179]. In particular, in [179], the relaxation of HK has been investigated with a technique different from the one employed in [171, 172] but with similar results. The problem of scattering of fermions in the background of hypermagnetic fields has been also studied in [180, 181].
Hypermagnetic knots with large correlation scale can be also generated dynamically provided an unknotted hypermagnetic background is already present.
Let us assume that dynamical pseudoscalar particles are evolving in the background geometry given by Eq. (5.1). The pseudoscalars are not a source of the background (i.e. they do not affect the time evolution of the scale factor) but, nonetheless, they evolve according to their specific dynamics and can excite other degrees of freedom.
The action describing the interaction of a dynamical pseudoscalar with hypercharge fields can be written as
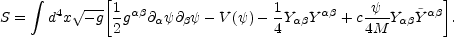 |
(5.120) |
This action is quite generic. In the case
V( )
= (m2 / 2)
)
= (m2 / 2)
 2
Eq. (5.120) is nothing but the curved
space generalization of the model usually employed in direct searches
of axionic particles
[182,
183,
184].
The constant in front of the anomaly
is a model-dependent factor. For example, in the case of axionic particles,
for large temperatures T
2
Eq. (5.120) is nothing but the curved
space generalization of the model usually employed in direct searches
of axionic particles
[182,
183,
184].
The constant in front of the anomaly
is a model-dependent factor. For example, in the case of axionic particles,
for large temperatures T
 mW,
the Abelian gauge fields present in Eq. (5.120) will be
hypercharge fields and
c = c
mW,
the Abelian gauge fields present in Eq. (5.120) will be
hypercharge fields and
c = c Y
Y
 ' /
(2
' /
(2  ) where
) where
 ' = g'2
/ 4
' = g'2
/ 4 and
c
and
c Y is a numerical factor of order 1
which can be computed (in a specific axion scenario) by knowing the
Peccei-Quinn charges of all the fermions present in the model
[185,
186].
For small temperatures T
Y is a numerical factor of order 1
which can be computed (in a specific axion scenario) by knowing the
Peccei-Quinn charges of all the fermions present in the model
[185,
186].
For small temperatures T  mW we have that the Abelian fields present in the
action (5.120) will coincide with ordinary electromagnetic fields and
c = c
mW we have that the Abelian fields present in the
action (5.120) will coincide with ordinary electromagnetic fields and
c = c

 em /
2
em /
2 where
where
 em
is the fine structure constant and
c
em
is the fine structure constant and
c
 is again a numerical factor.
is again a numerical factor.
The coupled system of equations describing the evolution of the
pseudoscalars
and of the Abelian gauge fields can be easily derived by varying the action
with respect to  and Yµ,
and Yµ,
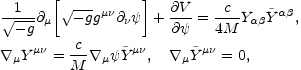 |
(5.121) |
where,
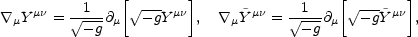 |
(5.122) |
are the usual covariant derivatives defined from the background FRW metric Eqs. (5.121) can be written in terms of the physical gauge fields
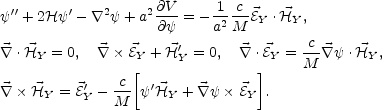 |
(5.123) |
We want now to study the amplification of gauge field
fluctuations induced by
the time evolution of
 . Then, the
evolution equation for the hypermagnetic fluctuations
. Then, the
evolution equation for the hypermagnetic fluctuations
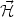 Y
can be obtained by linearizing Eqs. (5.123). We will assume that any
background gauge field is absent. In the linearisation procedure we will
also assume that the pseudoscalar field can be treated as completely
homogeneous (i.e.
|
Y
can be obtained by linearizing Eqs. (5.123). We will assume that any
background gauge field is absent. In the linearisation procedure we will
also assume that the pseudoscalar field can be treated as completely
homogeneous (i.e.
|
 | <<
| <<
 '). This seems
to be natural if,
prior to the radiation dominated epoch, an inflationary phase diluted
the gradients of the pseudoscalar.
'). This seems
to be natural if,
prior to the radiation dominated epoch, an inflationary phase diluted
the gradients of the pseudoscalar.
In this approximation, the result of the linearization can be simply written
in terms of the vector potentials in the gauge
Y0 = 0 and
 .
. 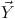 = 0:
= 0:
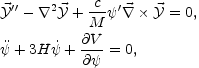 |
(5.124) (5.125) |
By combining the evolution equations for the gauge fields we can find a
decoupled evolution equation for
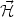 Y,
Y,
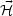 |
(5.126) |
From this equation is already apparent that the pseudo-scalar vertex
induces an interaction in the two physical polarizations of the
hypermagnetic field. Giving initial conditions which are such that
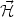 Y
Y
 0 with
0 with
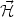 Y
.
Y
.
 ×
×
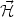 Y
= 0 a profile with
Y
= 0 a profile with
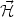 Y
.
Y
.
 ×
×
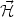 Y
Y
 0 can be generated provided
0 can be generated provided
 '
'
 0.
0.
23 This
temperature depends on the particle physics model, see also the
discussion reported in Section 5. In the MSM
TR  80 TeV
[167,
168,
169].
Back.
80 TeV
[167,
168,
169].
Back.
24 In order to interpret these solutions it is very interesting to make use of the Clebsh decomposition. The implications of this decomposition (beyond the hydrodynamical context, where it was originally discovered) have been recently discussed (see [177] and references therein). Back.