


Since the flux is conserved the ratio between the magnetic energy
density,  B(L,
B(L, ) and the energy density sitting in radiation,
) and the energy density sitting in radiation,

 (
( )
is almost constant and therefore, in terms of this quantity (which is
only scale dependent but not time dependent), the most simplistic
dynamo requirement can be rephrased (see
Section 3) as
)
is almost constant and therefore, in terms of this quantity (which is
only scale dependent but not time dependent), the most simplistic
dynamo requirement can be rephrased (see
Section 3) as
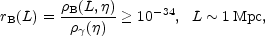 |
(6.1) |
to be compared with the value rB ~ 10-8 which would lead to the galactic magnetic field only thanks to the collapse and without the need of dynamo action (this would be the case when the magnetic field is fully primordial). Notice that Eq. (6.1) assumes that the magnetic flux is exactly frozen into the plasma element.
As previously pointed out during the discussion of the dynamo mechanism, the requirement expressed by Eq. (6.1) is unrealistic: it would correspond to thirty e-folds of amplification during galactic rotation and perfect flux freezing during the collapse of the protogalaxy. In a more realistic situation situation, taking into account the effectively achievable amplification of the dynamo action the requirement would rather be, prior to collapse,
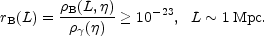 |
(6.2) |
In spite of the richness of the theoretical models, the mechanisms for magnetic field generation can be divided, broadly speaking, into two categories: astrophysical and cosmological. The cosmological mechanisms can be divided, in turn, into causal mechanisms (where the magnetic seeds are produced at a given time inside the horizon) and inflationary mechanisms where correlations in the magnetic field are produced outside the horizon.