2. ASTRONOMY MADE SIMPLE (FOR PHYSICISTS)

I think that it is fair to assume that most of you are physicists, so I begin by defining some of the units and terminology used by astronomers. I do this because much of this terminology is arcane for those not in the field.

First of all there is the peculiar logarithmic scale of flux - magnitudes - whereby a factor of 100 in flux is divided into five equal logarithmic intervals. The system is ancient and has its origin in the logarithmic response of the human eye. The ratio of the flux of two objects is then given by a difference in magnitudes; i.e.,

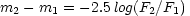(2.1)

where, one will notice, smaller magnitude means larger flux. The zero-point of this logarithmic scale is set by some standard star such as Vega. Because this is related to the flux, and not the luminosity of an object, it is called the "apparent" magnitude. Distant galaxies have apparent magnitudes, in visible light, of greater than 20, and the galaxies in the Hubble Deep Field, go down to magnitudes of 30. The magnitude is typically measured over a specified wavelength range or color band, such as blue (B), visual (V), or infrared (K), and these are designated m_B, m_V, and m_K, or sometimes just B,V, and K. This is made more confusing by the fact that there are several competing photometric systems (or sets of filters) and conversion between them is not always simple.

With a particular photometric system one can measure the color of an astronomical object, expressed as difference in magnitudes in two bands, or color index; e.g.,

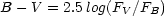(2.2)

Here a larger B-V color index means that an object is relatively redder; a smaller B-V that the object is bluer. Unlike the apparent magnitude, this is an intrinsic property of the object. Or rather, it is intrinsic once the astronomer corrects the magnitudes in the various bands to the zero-redshift (z = 0) frame. This is called the "K-correction" and requires a knowledge of the intrinsic spectral energy distribution (SED) of the source, be it a galaxy or a distant supernova.

The luminosity of an object is also an intrinsic property and is usually expressed by astronomers as an "absolute" magnitude. This is the apparent magnitude an object would have if it were placed at a standard distance, taken to be 10 parsecs, i.e. 3 × 10¹⁷ m (more on parsecs below). Because this distance is small by extragalactic standards the absolute magnitudes of galaxies turn out to be rather large negative numbers: M_G -18 to -21. The luminosity of a galaxy L_G in units of the solar luminosity L can be determined from the relation

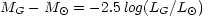(2.3)

where the absolute magnitude of the sun (in the V band) is 5.5. The luminosities of galaxies typically range from 10⁸ to 10¹¹ L. The peak absolute magnitude of a type I supernova (SNIa) is about -19.5, or comparable to an entire galaxy. This is one reason why these objects are such ideal extragalactic distance probes.

The unit of distance used by astronomers is also archaic: the parsec which is about 3 × 10¹⁶ m or about 3 light years. This is the distance to a star with an semi-annual parallax of 1 arc second and is not a bad unit when one is discussing the very local region of the galaxy. Our galaxy has a diameter between 10 to 20 kiloparsecs, so the kiloparsec is an appropriate unit when discussing galactic structure. The appropriate unit of extragalactic distance, however, is the "megaparsec" or Mpc, with nearby galaxies being those at distances less than 10 Mpc. The nearest large cluster of galaxies, the Virgo cluster, is at a distance of 20 Mpc, and very distant galaxies are those further than 100 Mpc, although here one has to be careful about how distance is operationally defined.

We all know that the Universe is uniformly expanding and the Hubble parameter, H, is the recession velocity of galaxies per unit distance, with H_o being its value in the present Universe. It is typically measured in units of km s^-1 Mpc^-1 or inverse time. A number of observations point to H_o 70 km s^-1 Mpc^-1 . The Hubble time is defined as t_H = H_o^-1 which is about 9.8 × 10⁹ h^-1 years, and this must be comparable to the age of the Universe. The definition h = H_o / 100 km s^-1 Mpc^-1 is a relic of the recent past when the Hubble parameter was less precisely determined, but I keep using it below because it remains convenient as a unit-less quantity. We can also define a characteristic scale for the universe which is the Hubble radius or r_H = c / H_o and this is 3000 h^-1 Mpc. This would be comparable to the "distance" to the horizon.

Just for interest, one could also define a Hubble acceleration or a_H = cH_o 7 × 10^-10 m/s². This modest acceleration of 7 angstroms/second squared is, in effect, the acceleration of the Hubble flow at the horizon if we live in a Universe dominated by a cosmological constant as observations seem to suggest. It is also comparable to the acceleration in the outer parts of galaxies where the need for dark matter first becomes apparent [13]. In some sense, it is remarkable that such a small acceleration has led to a major paradigm shift.