3. BASICS OF FRW COSMOLOGY

The fundamental assumption underlying the construction of cosmological models is that of the cosmological principle: The Universe appears spatially isotropic in all its properties to all observers. The only metric which is consistent with this principle is the Robertson-Walker metric:

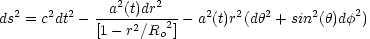(3.1)

where r is the radial comoving coordinate, a(t) is the dimensionless scale factor by which all distances vary as a function of cosmic time, and R_o^-2 is a parameter with dimensions of inverse length squared that describes the curvature of the Universe and may be positive, zero, or negative (see [14] for a general discussion).

This is the geometry of the Universe, but dynamics is provided by General Relativity - the Einstein field equations - which yield ordinary differential equations for a(t). The time-time component leads to a second order equation:

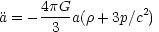(3.2)

where is the density, p is the pressure and the quantity in parenthesis is the active gravitational mass density. Considering conservation of energy for a perfect fluid

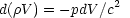(3.3)

with an equation of state

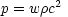(3.4)

we have a^-1(1+w). The equation of state combined with eq. 3.2 tells us that the Universe is accelerating if w < - 1/3.

The space-space components combined with the time-time component yield the usual first-order Friedmann equation

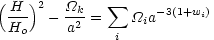(3.5)

where H = / a is the running Hubble parameter, the summation is over the various fluids comprising the Universe and

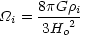(3.6)

with _k = - (r_H / R_o)². We often see eq. 3.5 written in terms of redshift where a = (1 + z)^-1. Each component has its own equation of state parameter, w_i: w = 0 for non-relativistic matter (baryons, CDM); w = 1/3 for radiation or other relativistic fluid; w = -1 for a cosmological constant; and -1 < w < -1/3 for "quintessence", dynamic dark energy resulting in ultimate acceleration of the universal expansion. I will not consider w < - 1 which has been termed "phantom" dark energy [15]; here the effective density increases as the Universe expands (this could be realized by a ghost field, a scalar with a kinetic term in the Lagrangian having the wrong sign so it rolls up rather than down a potential hill).

Given a universe composed of radiation, non-relativistic matter, and quintessence, the Friedmann equation takes its familiar form:

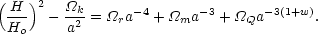(3.7)

Here it is evident that radiation drives the expansion at early times (a << 1), non-relativistic matter at later times, a non-vanishing curvature (_k 0) at later times still, and, if w < -1/3, the vacuum energy density ultimately dominates. For the purpose of this lecture, I refer to eq. 3.7 with w = -1 (the usual cosmological constant) as standard FRW cosmology, while 0 > w -1 would represent a minimal modification to FRW cosmology. Moreover, when w = -1, I replace _Q by . I will not consider changes to the Friedmann equation which might result from modified gravitational physics.

Because the subject here is observational cosmology we must discuss the operational definitions of distance in an FRW Universe. If there exists a standard meter stick, an object with a known fixed linear size d which does not evolve with cosmic time, then one could obviously define an angular size distance:

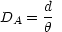(3.8)

where would be the observed angle subtended by this object. If there exists a standard candle, an object with a known fixed luminosity L which does not vary with cosmic time, then one could also define a luminosity distance:

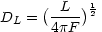(3.9)

where F is the measured flux of radiation.

For a RW universe both the angular size distance and the luminosity distance are related to the radial comoving coordinate,

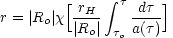(3.10)

where = tH_o, R_o² = - r_H² / _k, and

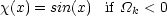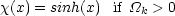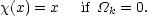Then it is the case that

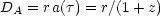(3.11a)

and

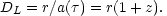(3.11b)

It is evident that both the angular size distance and the luminosity distance depend upon the expansion history (through d / a()) and the curvature (through (x)).

The same is true of a comoving volume element:

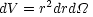(3.12)

where here d is an incremental solid angle. Therefore, if there exists a class of objects with a non-evolving comoving density, then this leads to another possible cosmological test: simply count those objects as a function of redshift or flux.

Below, I am going to consider these measures of distance and volume in the form of three classical cosmological tests:

1. Angular size tests which essentially involve the determination of D_A(z). Here one measure for objects with a known and (hopefully) standard linear size (such as compact radio sources).

2. Luminosity distance tests which involve the measurement of F(z) for presumably standard candles (such as supernova type Ia, SNIa).

3. dV/dz test which involve the counts of very faint galaxies as a function of flux and redshift.

But before I come to these classic tests, I want to discuss the evidence supporting the validity of the standard hot Big Bang, as an appropriate description of the early pre-recombination Universe.