5. THE POST-RECOMBINATION UNIVERSE: DETERMINATION OF H_o AND t_o

Certainly the most basic of the cosmological parameters is the present expansion rate, H_o, because this sets the scale of the Universe. Until a few years ago, there was a factor of two uncertainty in H_o; with two separate groups claiming two distinct values, one near 50 km s^-1 Mpc^-1 and the other nearer 100 km s^-1 Mpc^-1, and the errors quoted by both groups were much smaller than this factor of two difference. This points out a problem which is common in observational cosmology (or indeed, astronomy in general). Often the indicated statistical errors give the impression of great precision, whereas the true uncertainty is dominated by poorly understood or unknown systematic effects. That was true in the Hubble constant controversy, and there is no less reason to think that this problem is absent in modern results. I will return to this point several times below.

The great leap forward in determination of H_o came with the Hubble Space Telescope (HST) program on the distance scale. Here a particular kind of variable stars - Cepheid variables - were observed in twenty nearby spiral galaxies. Cepheids exhibit periodic variations in luminosity by a factor of two on timescales of 2-40 days. There is a well-determined empirical correlation between the period of Cepheids and their mean luminosity - the longer the period the higher the luminosity. Of course, this period - luminosity relation must be calibrated by observing Cepheids in some object with a distance known by other techniques and this remains a source of systematic uncertainty. But putting this problem aside, the Hubble Space telescope measured the periods and the apparent magnitudes, without confusion from adjacent bright stars, of a number of Cephieds in each of these relatively nearby galaxies, which yielded a distance determination (eq. 3.9). These galaxies are generally too close (less than 15 Mpc) to sample the pure Hubble flow - the Hubble flow on these scales is contaminated by random motion of the galaxies and systematic cosmic flows - but these determinations do permit a calibration of other secondary distance indicators which reach further out, such as supernovae type Ia (SNIa) and the Tully-Fisher relation (the observed tight correlation between the rotation velocities of a spiral galaxies and their luminosities). After an enormous amount of work by a number of very competent astronomers [28], the answer turned out to be h = 0.72 ± .10

As I mentioned there is the known systematic uncertainty of calibrating the period-luminosity relation, but there are other possible systematic effects that are less well-understood: How can we be certain that the period-luminosity relation for Cepheids is the same in all galaxies? For example, is this relation affected by the concentration of elements heavier than helium (the metallicity)? In view of such potential problems, other more direct physical methods, which by-pass the traditional "distance ladder" are of interest. Chief among these is the Sunyaev-Zeldovich (S-Z) effect which is relevant to clusters of galaxies [29]. The baryonic mass of clusters of galaxies is primarily in the form of hot gas, which typically exceeds the mass in the visible galaxies by more than a factor of two. This gas has a temperature between 10⁷ and 10⁸ K (i.e., the sound speed is comparable to the one-dimensional velocity dispersion of the galaxies) and is detected by satellite X-ray telescopes with detectors in the range of several KeV. The S-Z effect is a small change in the intensity of the CMB in the direction of such clusters due to Compton scattering of CMB photons by thermal electrons (classical electron scattering would, of course, produce no intensity change). Basically, CMB photons are moved from the Rayleigh-Jeans part of the black body spectrum to the Wien part, so the effect is observable as a spectral distortion of the black body spectrum in the range of 100 to 300 GHz. It is a small effect (on the order of 0.4 milli Kelvin) but still 5 to 10 times larger than the intrinsic anisotropies in the CMB.

By measuring the amplitude of the S-Z effect one determines an optical depth

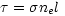(5.1)

where is the frequency dependent cross section, l is the path length, and n_e is the electron density. Because these same clusters emit X-rays via thermal bremsstrahlung, we may also determine, from the observed X-ray intensity, an emission measure:

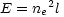(5.2)

Here we have two equations for two unknowns, n_e and l. (This is simplifying the actual calculation because n_e is a function of radius in the cluster.) Knowing l and the angular diameter of the cluster we can then calculate the angular size distance to the cluster via eq. 3.8. Hence, the Hubble parameter is given by H_o = v / D_A where v is the observed recession velocity of the cluster. All of this assumes that the clusters have a spherical shape on average, so the method needs to be applied to a number of clusters. Even so biases are possible if clusters have more typically a prolate shape or an oblate shape, or if the X-ray emitting gas is clumpy. Overall, for a number of clusters [30] the answer turns out to be h = 0.6 - somewhat smaller than the HST distance ladder method, but the systematic uncertainties remain large.

A second direct method relies on time delays in gravitational lenses [31]. Occasionally, a distant quasar (the source) is lensed by an intervening galaxy (the lens) into multiple images; that is to say, we observe two or more images of the same background object separated typically by one or two seconds of arc. This means that there are two or more distinct null geodesics connecting us to the quasar with two or more different light travel times. Now a number of these quasars are intrinsically variable over time scales of days or months (not periodic but irregular variables). Therefore, in two distinct images we should observe the flux variations track each other with a time delay. This measured delay is proportional to the ratio D_l D_s / D_ls where these are the angular size distances to the lens, the source, and the lens to the source. Since this ratio is proportional to H_o^-1, the measured time delay, when combined with a mass model for the lens (the main source of uncertainty in the method), provides a determination of the Hubble parameter. This method, applied to several lenses [32, 33], again tends to yield a value of h that is somewhat smaller than the HST value, i.e., 0.6. In a recent summary [34] it is claimed that, for four cases where the lens is an isolated galaxy, the result is h = 0.48 ± .03, if the overall mass distribution in each case can be represented by a singular isothermal sphere. On the other hand, in a well-observed lens where the mass distribution is constrained by observations of stellar velocity dispersion [35], the implied value of h is 0.75^+.07_-.06. Such supplementary observations are important because the essential uncertainty with this technique is in the adopted mass model of the lens.

It is probably safe to say that h 0.7, with an uncertainty of 0.10 and perhaps a slight bias toward lower values, but the story is not over as S-Z and gravitational lens determinations continue to improve. This is of considerable interest because the best fit to the CMB anisotropies observed by WMAP implies that h = 0.72 ± .05 in perfect agreement with the HST result. With the S-Z effect and lenses, there remains the possibility of a contradiction.

With h = .70, we find a Hubble time of t_H = 14 Gyr. Now in FRW cosmology, the age of the Universe is t_o = f t_H where f is a number depending upon the cosmological model. For an Einstein-de Sitter Universe (i.e., _k = 0, _Q = 0, _m = 1) f = 2/3 which means that t_o = 9.1 Gyr. For an empty negatively curved Universe, f = 1 which means that the age is the Hubble time. Generally, models with a dominant vacuum energy density (_Q 1, w -1) are older (f 1) and for the concordance model, f = 0.94. Therefore, independent determinations of the age of the Universe are an important consistency test of the cosmology.

It is reasonable to expect that the Universe should be older than the oldest stars it contains, so if we can measure the ages of the oldest stars, we have, at least, a lower limit on the age of the Universe. Globular star clusters are old stellar systems in the halo of our own galaxy; these systems are distributed in a roughly spherical region around the galactic disk and have low abundances of heavy elements suggesting they were formed before most of the stars in the disk. If one can measure the luminosity, L_u, of the most luminous un-evolved stars in a globular cluster (that is, stars still burning hydrogen in their cores), then one may estimate the age. That is because this luminosity is correlated with age: a higher L_u means a younger cluster. Up to five years ago, this method yielded globular cluster ages of t_gc 14 ± 2 Gyr, which, combined with the Hubble parameter discussed above, would be in direct contradiction with the Einstein-de Sitter _m = 1 Universe. But about ten years ago the Hipparchus satellite began to return accurate parallaxes for thousands of relatively nearby stars which led to a recalibration of the entire distance scale. Distances outside the solar system increased by about 10% (in fact, the entire Universe suddenly grew by this same factor leading to a decrease in the HST value for the Hubble parameter). This meant that the globular clusters were further away, that L_u was 20% larger, and the clusters were correspondingly younger: t_gc 11.5 ± 1.3 Gyr. If we assume that the Universe is about 1 Gyr older than the globular clusters, then the age of the Universe becomes 12.5 ± 2 Gyr [36] which is almost consistent with the Einstein-de Sitter Universe. At least there is no longer any compelling time scale argument for a non-zero vacuum energy density, _Q > 0. The value of accurate basic astronomical data (and what is more basic than stellar positions?) should never be underestimated.

A second method for determining the ages of stars is familiar to all physicists, and that is radioactive dating. This has been done recently by observations of a U²³⁸ line in a metal-poor galactic star (an old star). Although the iron abundance in this star is only 1/800 that of the sun, the abundances of a group of rare earth metals known as r-process elements are enhanced. The r-process is rapid neutron absorption onto iron nuclei (rapid compared to the timescale for subsequent decay) which contributes to certain abundance peaks in the periodic table and which occurs in explosive events like supernovae. This means that this old star was formed from gas contaminated by an even older supernova event; i.e. the uranium was deposited at a definite time in the past. Now U²³⁸ is unstable with a half life of 4.5 Gyr which makes it an ideal probe on cosmological times scales. All we have to do is compare the observed abundance of U²³⁸ to that of a stable r-process element (in this case osmium), with what is expected from the r-process. The answer for the age of this star (or more accurately, the SN which contaminated the gas out of which the star formed) is 12.5 ± 3 Gyr, which is completely consistent with the globular cluster ages [37].

If we take 0.6 < h < 0.7, and 9.5 Gyr < t_o < 15.5 Gyr this implies that 0.59 < H_o t_o < 1.1. This is consistent with a wide range of FRW cosmologies from Einstein-de Sitter to the concordance model. That is to say, independent measurements of H_o and t_o are not yet precise enough to stand as a confirmation or contradiction to the WMAP result.