4. OBSERVATIONAL SUPPORT FOR THE STANDARD MODEL OF THE EARLY UNIVERSE

The discovery 40 years ago of the cosmic microwave background radiation (CMB) ended, for most people, the old debate about Steady-State vs. the Hot Big Bang. Ten years ago, support for the Hot Big Bang was fortified by the COBE satellite which demonstrated that the CMB has a Planck spectrum to extremely high precision; it is, quite literally, the most perfect black body observed in nature [16]. This makes any model in which the CMB is produced by some secondary process, such as thermal re-radiation of starlight by hot dust, seem extremely difficult, if not impossible, to contrive.

Not only does the background radiation have a thermal spectrum, it is now evident that this radiation was hotter in the past than now as expected for adiabatic expansion of the Universe. This is verified by observations of neutral carbon fine structure lines as well as molecular hydrogen rotational transitions in absorption line systems in the spectra of distant quasars. Here, the implied population of different levels, determined primarily by the background radiation field, is an effective thermometer for that radiation field. One example is provided by a quasar with an absorption line system at z = 3.025 which demonstrates that the temperature of the CMB at this redshift was 12.1^+1.7_-8.2 K, consistent with expectations (T 1 + z) [17].

However, the most outstanding success story for the Hot Big Bang is generally considered to be that of Big Bang Nucleosynthesis (BBN) which, for a given number of relativistic particle species, predicts the primordial abundances of the light isotopes with, effectively, one free parameter: the ratio of baryons-to-photons, [18]. I want to review this success story, and point out that there remains one evident inconsistency which may be entirely observational, but which alternatively may point to new physics.

We saw above in the Friedmann equation (eq. 3.7) that radiation, if present, will always dominate the expansion of the Universe at early enough epochs (roughly at z 2 × 10⁴ _m.) This makes the expansion and thermal history of the Universe particularly simple during this period. The Friedmann equation becomes

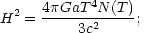(4.1)

here a is the radiation constant and N(T) is the number of degrees of freedom in relativistic particles. The scale factor is seen to grow as t^1/2 which means that the age of the Universe is given by t = 1/2H. This implies, from eq. 4.1, an age-temperature relation of the form t T^-2. Putting in numbers, the precise relation is

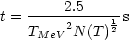(4.2)

where the age is given in seconds and T_MeV is the temperature measured in MeV. It is only necessary to count the number of relativistic particle species:

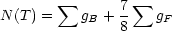(4.3)

where the sums are over the number of bosonic degrees of freedom (g_B) and fermionic degrees of freedom (g_F). The factor 7/8 is due to the difference in Bose-Einstein and Fermi-Dirac statistics. Adding in all the known species - photons, electrons-positrons (when T_MeV > 0.5), three types of neutrinos and anti-neutrinos - we find

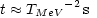(4.4)

for the age-temperature relation in the early Universe.

When the Universe is less than one second old (T > 1 MeV) the weak interactions

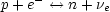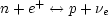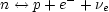are rapid enough to establish equilibrium between these various species. But when T falls below 1 MeV, the reaction rates become slower than the expansion rate of the Universe, and neutrons "freeze out" - they fall out of thermal equilibrium, as do the neutrinos. This means the equilibrium ratio of neutrons to protons at T 1 MeV is frozen into the expanding soup: n / p 0.20 - 0.25. You all know that neutrons outside of an atomic nucleus are unstable particles and decay with a half-life of about 15 minutes. But before that happens there is a possible escape route:

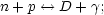that is to say, a neutron can combine with a proton to make a deuterium nucleus and a photon. However, so long as the mean energy of particles and photons is greater than the binding energy of deuterium, about 86 Kev, the inverse reaction happens as well; as soon as a deuterium nucleus is formed it is photo-dissociated. This means that it is impossible to build up a significant abundance of deuterium until the temperature of the Universe has fallen below 86 KeV or, looking back at eq. 4.4, until the Universe has become older than about 2.5 minutes. Then all of the remaining neutrons are rapidly processed into deuterium.

But the deuterium doesn't stay around for long either. Given the temperature and particle densities prevailing at this epoch, there are a series of two-body reactions by which two deuterons combine to make He⁴ and trace amounts of lithium and He³. These reactions occur at a rate which depends upon the overall abundance of baryons, the ratio of baryons to photons:

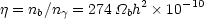(4.5)

So essentially all neutrons which survive until T = 86 KeV become locked up in He⁴. Therefore, the primordial abundance of helium depends primarily upon the expansion rate of the Universe: the faster the expansion (due, say, to more neutrino types or to a larger constant of gravity) the more helium. The abundance of remaining deuterium, however, depends upon the abundance of baryons, : the higher the less deuterium. This is why it is sometimes said [18] that the abundance of primordial helium is a good chronometer (it measures the expansion rate), while the abundance of deuterium is a good baryometer (it measures _b). This is evident in Figs. 1 and 2 where we see first the predicted abundances of various light isotopes as a function of , and secondly, the predicted abundance of He vs. that of deuterium for two, three and four neutrino types.

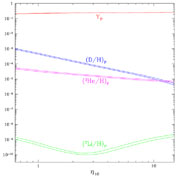Figure 1. The predicted abundances of the light isotopes as a function of [18]. Here Yp is the predicted mass fraction of helium and is based upon the assumption of three neutrino types. The widths of the bands show the theoretical uncertainty.

Figure 2. The predicted abundance, Yp, of helium (the mass fraction) as a function of the predicted deuterium abundance for two, three, and four neutrino types [18]. The point with error bars is the observed abundances of helium and deuterium.

The determination of primordial abundances is not a straightforward matter because the abundance of these elements evolves due to processes occurring within stars ("astration"). In general, the abundance of helium increases (hydrogen is processed to helium providing the primary energy source for stars), while deuterium is destroyed by the same process. This means that astronomers, when trying to estimate primordial abundances of deuterium or helium, must try to find pristine, unprocessed material, in so far as possible. One way to find unprocessed material is to look back at early times, or large redshift, before the baryonic material has been recycled through generations of stars. This can be done with quasar absorption line systems, where several groups of observers have been attempting to identify very shallow absorption lines of deuterium at the same redshift as the much stronger hydrogen Lyman alpha absorption line systems [19, 20, 21, 22]. It is a difficult observation requiring the largest telescopes; the lines identified with deuterium might be mis-identified weak hydrogen or metal lines (incidentally, for an astronomer, any element heavier than helium is a metal). Taking the results of various groups at face value, the weighted mean value [18] is D/H 2.6 ± 0.3 × 10^-5. Looking back at Fig. 1, we see that this would correspond to = 6.1 ± 0.6 × 10^-10 or _b h² = 0.022 ± 0.003.

A word of caution is necessary here: the values for the deuterium abundance determined by the different groups scatter by more than a factor of two, which is considerably larger than the quoted statistical errors ( 25%). This indicates that significant systematic effects are present. But it is noteworthy that the angular power spectrum of the CMB anisotropies also yields an estimate of the baryon abundance; this is encoded in the ratio of the amplitudes of the second to first peak. The value is _b h² = 0.024 ± 0.001. In other words, the two determinations agree to within their errors. This is quite remarkable considering that the first determination involves nuclear processes occurring within the first three minutes of the Big Bang, and the second involves oscillations of a photon-baryon plasma on an enormous scale when the Universe is about 500,000 years old. If this is a coincidence, it is truly an astounding one.

So much for the baryometer, but what about the chronometer - helium? Again astronomers are obliged to look for unprocessed material in order to estimate the primordial abundance. The technique of looking at quasar absorption line systems doesn't work for helium because the absorption lines from the ground state are far in the ultraviolet - about 600 Å for neutral helium and, more likely, 300 Å from singly ionized helium. This is well beyond the Lyman limit of hydrogen, where the radiation from the background quasar is effectively absorbed [23]. Here the technique is to look for He emission lines from HII regions (ionized gas around hot stars) in nearby galaxies and compare to the hydrogen emission lines. But how does one know that the gas is unprocessed? The clue is in the fact that stars not only process hydrogen into helium, but they also, in the late stages of their evolution, synthesize heavier elements (metals) in their interiors. Therefore the abundance of heavier elements, like silicon, is an indicator of how much nuclear processing the ionized gas has undergone. It is observed that the He abundance is correlated with the metal abundance; so the goal is to find HII regions with as low a metal abundance as possible, and then extrapolate this empirical correlation to zero metal abundance [24, 25]. The answer turns out to be He/H 0.24, which is shown by the point with error bars in Fig. 2.

This value is embarrassingly low, given the observed deuterium abundance. It is obviously more consistent with an expansion rate provided by only two neutrino types rather than three, but we know that there are certainly three types. Possible reasons for this apparent anomaly are:

1) Bad astronomy: There are unresolved systematic errors in determination of the relative He abundance in HII regions indicated by the fact that the results of different groups differ by more than the quoted statistical errors [18]. The derivation of the helium to hydrogen ratio from the observed He⁺/H⁺ ratio requires some understanding of the structure of the HII regions. If there are relatively cool ionizing stars (T < 35000 K) spatially separated from the hotter stars, there may be relatively less He⁺ associated with a given abundance of H⁺. Lines of other elements need to be observed to estimate the excitation temperature; it is a complex problem.

2) New neutrino physics: There may be an asymmetry between neutrinos and anti-neutrinos (something like the baryon-antibaryon asymmetry which provides us with the observed Universe). This would manifest itself as a chemical potential in the Boltzmann equation giving different equilibrium ratios of the various neutrino species [26].

3) New gravitational physics: any change in the gravitational interaction which is effective at early epochs (braneworld effects?) could have a pronounced effect on nucleosynthesis. For example, a lower effective constant of gravity would yield a lower expansion rate and a lower He abundance. The standard minimal braneworld correction term, proportional to the square of the density [27], goes in the wrong direction.

It is unclear if the low helium abundance is a serious problem for the standard Big Bang. But it is clear that the agreement of the implied baryon abundance with the CMB determination is an impressive success, and strongly supports the assertion that the Hot Big Bang is the correct model for the pre-recombination Universe.