4.8. Baryogenesis

The symmetry between particles and antiparticles [126, 127], firmly established in collider physics, naturally leads to the question of why the observed universe is composed almost entirely of matter with little or no primordial antimatter.

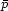Outside of particle accelerators, antimatter can be seen in cosmic rays in the form of a few antiprotons, present at a level of around 10^-4 in comparison with the number of protons (for example see [128]). However, this proportion is consistent with secondary antiproton production through accelerator-like processes, p + p 3p + , as the cosmic rays stream towards us. Thus there is no evidence for primordial antimatter in our galaxy. Also, if matter and antimatter galaxies were to coexist in clusters of galaxies, then we would expect there to be a detectable background of -radiation from nucleon-antinucleon annihilations within the clusters. This background is not observed and so we conclude that there is negligible antimatter on the scale of clusters (For a review of the evidence for a baryon asymmetry see [129].)

More generally, if large domains of matter and antimatter exist, then annihilations would take place at the interfaces between them. If the typical size of such a domain was small enough, then the energy released by these annihilations would result in a diffuse -ray background and a distortion of the cosmic microwave radiation, neither of which is observed.

While the above considerations put an experimental upper bound on the amount of antimatter in the universe, strict quantitative estimates of the relative abundances of baryonic matter and antimatter may also be obtained from the standard cosmology. The baryon number density does not remain constant during the evolution of the universe, instead scaling like a^-3, where a is the cosmological scale factor [130]. It is therefore convenient to define the baryon asymmetry of the universe in terms of the quantity

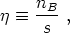(164)

defined earlier. Recall that the range of consistent with the deuterium and ³He primordial abundances is

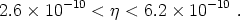(165)

Thus the natural question arises; as the universe cooled from early times to today, what processes, both particle physics and cosmological, were responsible for the generation of this very specific baryon asymmetry? (For reviews of mechanisms to generate the baryon asymmetry, see

As pointed out by Sakharov [131], a small baryon asymmetry may have been produced in the early universe if three necessary conditions are satisfied

• baryon number (B) violation,
• violation of C (charge conjugation symmetry) and CP (the composition of parity and C),
• departure from thermal equilibrium.

The first condition should be clear since, starting from a baryon symmetric universe with = 0, baryon number violation must take place in order to evolve into a universe in which does not vanish. The second Sakharov criterion is required because, if C and CP are exact symmetries, one can prove that the total rate for any process which produces an excess of baryons is equal to the rate of the complementary process which produces an excess of antibaryons and so no net baryon number can be created. That is to say that the thermal average of the baryon number operator B, which is odd under both C and CP, is zero unless those discrete symmetries are violated. CP violation is present either if there are complex phases in the Lagrangian which cannot be reabsorbed by field redefinitions (explicit breaking) or if some Higgs scalar field acquires a VEV which is not real (spontaneous breaking). We will discuss this in detail shortly.

Finally, to explain the third criterion, one can calculate the equilibrium average of B at a temperature T = 1 / :

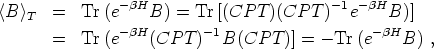(166)

where we have used that the Hamiltonian H commutes with CPT. Thus <B>_T = 0 in equilibrium and there is no generation of net baryon number.

Of the three Sakharov conditions, baryon number violation and C and CP violation may be investigated only within a given particle physics model, while the third condition - the departure from thermal equilibrium - may be discussed in a more general way, as we shall see (for baryogenesis reviews see [132, 133, 9, 10, 134, 135, 136].) Let us discuss the Sakharov criteria in more detail.