4.9. Baryon Number Violation

4.9.1. B-violation in Grand Unified Theories

As discussed earlier, Grand Unified Theories (GUTs) [137] describe the fundamental interactions by means of a unique gauge group G which contains the Standard Model (SM) gauge group SU(3)_C 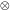SU(2)_L 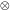U(1)_Y. The fundamental idea of GUTs is that at energies higher than a certain energy threshold M_GUT the group symmetry is G and that, at lower energies, the symmetry is broken down to the SM gauge symmetry, possibly through a chain of symmetry breakings. The main motivation for this scenario is that, at least in supersymmetric models, the (running) gauge couplings of the SM unify [138, 139, 140] at the scale M_GUT 2 × 10¹⁶ GeV, hinting at the presence of a GUT involving a higher symmetry with a single gauge coupling.

Baryon number violation seems very natural in GUTs. Indeed, a general property of these theories is that the same representation of G may contain both quarks and leptons, and therefore it is possible for scalar and gauge bosons to mediate gauge interactions among fermions having different baryon number.

4.9.2. B-violation in the Electroweak theory.

It is well-known that the most general renormalizable Lagrangian invariant under the SM gauge group and containing only color singlet Higgs fields is automatically invariant under global abelian symmetries which may be identified with the baryonic and leptonic symmetries. These, therefore, are accidental symmetries and as a result it is not possible to violate B and L at tree-level or at any order of perturbation theory. Nevertheless, in many cases the perturbative expansion does not describe all the dynamics of the theory and, indeed, in 1976 't Hooft [141] realized that nonperturbative effects (instantons) may give rise to processes which violate the combination B + L, but not the orthogonal combination B - L. The probability of these processes occurring today is exponentially suppressed and probably irrelevant. However, in more extreme situations - like the primordial universe at very high temperatures [142, 143, 144, 145] - baryon and lepton number violating processes may be fast enough to play a significant role in baryogenesis. Let us have a closer look.

At the quantum level, the baryon and the lepton symmetries are anomalous [146, 147], so that their respective Noether currents j_B^µ and j_L^µ are no longer conserved, but satisfy

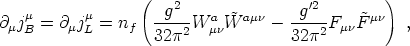(167)

where g and g' are the gauge couplings of SU(2)_L and U(1)_Y, respectively, n_f is the number of families and 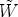^µ = (1/2)^µ W is the dual of the SU(2)_L field strength tensor, with an analogous expression holding for . To understand how the anomaly is closely related to the vacuum structure of the theory, we may compute the change in baryon number from time t = 0 to some arbitrary final time t = t_f. For transitions between vacua, the average values of the field strengths are zero at the beginning and the end of the evolution. The change in baryon number may be written as

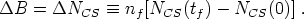(168)

where the Chern-Simons number is defined to be

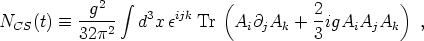(169)

where A_i is the SU(2)_L gauge field. Although the Chern-Simons number is not gauge invariant, the change N_CS is. Thus, changes in Chern-Simons number result in changes in baryon number which are integral multiples of the number of families n_f (with n_f = 3 in the real world). Gauge transformations U(x) which connects two degenerate vacua of the gauge theory may change the Chern-Simons number by an integer n, the winding number.

If the system is able to perform a transition from the vacuum 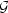_vac⁽ⁿ⁾ to the closest one 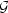_vac^(n±1), the Chern-Simons number is changed by unity and B = L = n_f. Each transition creates 9 left-handed quarks (3 color states for each generation) and 3 left-handed leptons (one per generation).

However, adjacent vacua of the electroweak theory are separated by a ridge of configurations with energies larger than that of the vacuum. The lowest energy point on this ridge is a saddle point solution to the equations of motion with a single negative eigenvalue, and is referred to as the sphaleron [143, 144]. The probability of baryon number nonconserving processes at zero temperature has been computed by 't Hooft [141] and is highly suppressed.

The thermal rate of baryon number violation in the broken phase is

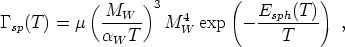(170)

where µ is a dimensionless constant. Although the Boltzmann suppression in (170) appears large, it is to be expected that, when the electroweak symmetry becomes restored at a temperature of around 100 GeV, there will no longer be an exponential suppression factor. A simple estimate is that the rate per unit volume of sphaleron events is

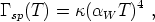(171)

with another dimensionless constant. The rate of sphaleron processes can be related to the diffusion constant for Chern-Simons number by a fluctuation-dissipation theorem [148] (for a good description of this see [134]).

4.9.3. CP violation

CP violation in GUTs arises in loop-diagram corrections to baryon number violating bosonic decays. Since it is necessary that the particles in the loop also undergo B-violating decays, the relevant particles are the X, Y, and H₃ bosons in the case of SU(5).

In the electroweak theory things are somewhat different. Since only the left-handed fermions are SU(2)_L gauge coupled, C is maximally broken in the SM. Moreover, CP is known not to be an exact symmetry of the weak interactions. This is seen experimentally in the neutral kaon system through K₀, 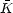₀ mixing. Thus, CP violation is a natural feature of the standard electroweak model.

While this is encouraging for baryogenesis, it turns out that this particular source of CP violation is not strong enough. The relevant effects are parameterized by a dimensionless constant which is no larger than 10^-20. This appears to be much too small to account for the observed BAU and, thus far, attempts to utilize this source of CP violation for electroweak baryogenesis have been unsuccessful. In light of this, it is usual to extend the SM in some fashion that increases the amount of CP violation in the theory while not leading to results that conflict with current experimental data. One concrete example of a well-motivated extension in the minimal supersymmetric standard model (MSSM).

4.9.4. Departure from Thermal Equilibrium

In some scenarios, such as GUT baryogenesis, the third Sakharov condition is satisfied due to the presence of superheavy decaying particles in a rapidly expanding universe. These generically fall under the name of out-of-equilibrium decay mechanisms.

The underlying idea is fairly simple. If the decay rate _X of the superheavy particles X at the time they become nonrelativistic (i.e. at the temperature T ~ M_X) is much smaller than the expansion rate of the universe, then the X particles cannot decay on the time scale of the expansion and so they remain as abundant as photons for T M_X. In other words, at some temperature T > M_X, the superheavy particles X are so weakly interacting that they cannot catch up with the expansion of the universe and they decouple from the thermal bath while they are still relativistic, so that n_X ~ n ~ T³ at the time of decoupling.

Therefore, at temperature T M_X, they populate the universe with an abundance which is much larger than the equilibrium one. This overabundance is precisely the departure from thermal equilibrium needed to produce a final nonvanishing baryon asymmetry when the heavy states X undergo B and CP violating decays.

The out-of-equilibrium condition requires very heavy states: M_X (10¹⁵ - 10¹⁶) GeV and M_X (10¹⁰ - 10¹⁶) GeV, for gauge and scalar bosons, respectively [149], if these heavy particles decay through renormalizable operators.

A different implementation can be found in the electroweak theory. At temperatures around the electroweak scale, the expansion rate of the universe in thermal units is small compared to the rate of baryon number violating processes. This means that the equilibrium description of particle phenomena is extremely accurate at electroweak temperatures. Thus, baryogenesis cannot occur at such low scales without the aid of phase transitions and the question of the order of the electroweak phase transition becomes central.

If the EWPT is second order or a continuous crossover, the associated departure from equilibrium is insufficient to lead to relevant baryon number production [145]. This means that for EWBG to succeed, we either need the EWPT to be strongly first order or other methods of destroying thermal equilibrium to be present at the phase transition. For a first order transition there is an extremum at = 0 which becomes separated from a second local minimum by an energy barrier. At the critical temperature T = T_c both phases are equally favored energetically and at later times the minimum at 0 becomes the global minimum of the theory.

The dynamics of the phase transition in this situation is crucial to most scenarios of electroweak baryogenesis. The essential picture is that around T_c quantum tunneling occurs and nucleation of bubbles of the true vacuum in the sea of false begins. Initially these bubbles are not large enough for their volume energy to overcome the competing surface tension and they shrink and disappear. However, at a particular temperature below T_c, bubbles just large enough to grow nucleate. These are termed critical bubbles, and they expand, eventually filling all of space and completing the transition.

As the bubble walls pass each point in space, the order parameter changes rapidly, as do the other fields, and this leads to a significant departure from thermal equilibrium. Thus, if the phase transition is strongly enough first order it is possible to satisfy the third Sakharov criterion in this way.

A further natural way to depart from equilibrium is provided by the dynamics of topological defects [150, 151, 152, 153]. If, for example, cosmic strings are produced at the GUT phase transition, then the decays of loops of string act as an additional source of superheavy bosons which undergo baryon number violating decays.

When defects are produced at the TeV scale, a detailed analysis of the dynamics of a network of these objects shows that a significant baryon to entropy ratio can be generated if the electroweak symmetry is restored around such a higher scale ordinary defect. Although B-violation can be inefficient along nonsuperconducting strings [154], there remain viable scenarios involving other ordinary defects, superconducting strings or defects carrying baryon number.

4.9.5. Baryogenesis via leptogenesis

Since the linear combination B - L is left unchanged by sphaleron transitions, the baryon asymmetry may be generated from a lepton asymmetry [155, 156, 157] (see also [158, 159].) Indeed, sphaleron transition will reprocess any lepton asymmetry and convert (a fraction of) it into baryon number. This is because B + L must be vanishing and the final baryon asymmetry results to be B - L.

In the SM as well as in its unified extension based on the group SU(5), B - L is conserved and no asymmetry in B - L can be generated. However, adding right-handed Majorana neutrinos to the SM breaks B - L and the primordial lepton asymmetry may be generated by the out-of-equilibrium decay of heavy right-handed Majorana neutrinos N_L^c (in the supersymmetric version, heavy scalar neutrino decays are also relevant for leptogenesis). This simple extension of the SM can be embedded into GUTs with gauge groups containing SO(10). Heavy right-handed Majorana neutrinos can also explain the smallness of the light neutrino masses via the see-saw mechanism [157].

4.9.6. Affleck-Dine Baryogenesis

Finally in this section, we mention briefly a mechanism introduced by Affleck and Dine [160] involving the cosmological evolution of scalar fields carrying baryonic charge.

Consider a colorless, electrically neutral combination of quark and lepton fields. In a supersymmetric theory this object has a scalar superpartner, , composed of the corresponding squark 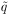and slepton 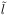fields.

An important feature of supersymmetric field theories is the existence of "flat directions" in field space, on which the scalar potential vanishes. Consider the case where some component of the field lies along a flat direction. By this we mean that there exist directions in the superpotential along which the relevant components of can be considered as a free massless field. At the level of renormalizable terms, flat directions are generic, but supersymmetry breaking and nonrenormalizable operators lift the flat directions and sets the scale for their potential.

During inflation it is likely that the field is displaced from the position <> = 0, establishing the initial conditions for the subsequent evolution of the field. An important role is played at this stage by baryon number violating operators in the potential V(), which determine the initial phase of the field. When the Hubble rate becomes of the order of the curvature of the potential ~ m_3/2, the condensate starts oscillating around its present minimum. At this time, B-violating terms in the potential are of comparable importance to the mass term, thereby imparting a substantial baryon number to the condensate. After this time, the baryon number violating operators are negligible so that, when the baryonic charge of is transferred to fermions through decays, the net baryon number of the universe is preserved by the subsequent cosmological evolution.

The most recent implementations of the Affleck-Dine scenario have been in the context of the minimal supersymmetric standard model [161, 162] in which, because there are large numbers of fields, flat directions occur because of accidental degeneracies in field space.