2.2. Continuum emission from dust

The dust emission process is thermal, with dust grains emitting a modified blackbody spectrum. Grains of interstellar dust, distributed throughout the ISM of a galaxy, are heated to temperatures between about 20 and 200 K, depending on the spectrum and intensity of the interstellar radiation field (ISRF), and the size and optical properties of the grains. Higher dust temperatures can be produced close to a powerful source of radiation, with dust subliming at temperatures of order 2000 K. Very small grains can be heated far above their equilibrium temperatures by absorbing hard-UV photons (see Draine and Li, 2001). Lower dust temperatures, always exceeding the CMB temperature, are possible in opaque regions of the ISM that are shielded from intense heating, in the intergalactic medium or in regions with an intrinsically weak ISRF. Unless dust is heated by the ISRF in addition to the CMB the galaxy will not be detectable. We now consider the properties of the dust emission that are relevant to observations of high-redshift galaxies.

2.2.1. The emission spectrum, dust mass and temperature

The minimum parameters necessary to describe the emission from dust grains are a temperature T_d and a form of the emissivity function . In any galaxy there will be a distribution of dust temperatures, reflecting the different nature and environment of each grain. It is useful to use T_d to describe the coolest grains that contribute significantly to the energy output of a galaxy when discussing submm observations. In most cases, spatially and spectrally resolved images of galaxies are not available, and so it is reasonable to assume a volume-averaged description of the emissivity function as a function of frequency , . Values of in the range 1-2 are usually assumed. Scattering theory predicts that 2 at low frequencies, while a value 1 at high frequencies matches the general trend of the interstellar extinction curve that describes the properties of absorption of optical and UV radiation by the ISM (see Calzetti et al., 2000 and Section 2 of the review by Franceschini, 2002).

The simplest form of the emission spectrum/SED, f is given by assuming that f B, in which B is the Planck function (2k T_d ² / c² in the Rayleigh-Jeans limit, in units of W m^-2 Hz^-1 sr^-1). This assumes that the emitting source is optically thin. For fitting spectra of galaxies found in deep submm surveys, we assume the simple B function to describe the SED. Dunne et al. (2000) and Dunne and Eales (2001) also use this functional form to fit the observed submm spectra of low-redshift galaxies. At the expense of adding another parameter to describe the SED, there is some physical motivation for a SED that includes an optical depth term,

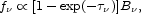(1)

where is the frequency-dependent optical depth of the cloud, and is a multiple of . This equation tends to the simpler B function at long wavelengths, and is assumed by, for example, Benford et al. (1999), Omont et al. (2001), Priddey and McMahon (2001) and Isaak et al. (2002), whose submm data for high-redshift AGNs tends to correspond to rest-frame frequencies that are relatively close to the peak of the SED. The extra parameter required to relate and can be defined as the frequency at which = 1 and the cloud becomes optically thick. If the opacity near a wavelength of 100 µm is large, then the form of the peak of the SED tends to that of a blackbody spectrum. This suppresses the emission near to the SED peak relative to the emission in the Rayleigh-Jeans regime, and so this functional form provides a good fit to a set of submm and far-IR data with a higher value of T_d as compared with the B function, usually by about 10-20%. However, because most observed SEDs for high-redshift galaxies have fewer than four data points (see Fig. 2), the difference is unlikely to be very significant.

It is reasonable to assume that the mid-IR SED can be smoothly interpolated from a modified blackbody function at low frequencies to a power-law f in the mid-IR waveband on the high-frequency side of the spectral peak, in order to prevent the high-frequency SED from falling exponentially with a Wien spectrum. Hotter components of dust, emitting at shorter wavelengths, and ultimately stellar emission in the near-IR waveband, are certain to be present to reduce the steepness of the SED in the Wien regime. That an exponential Wien spectrum is inappropriate can be seen from the well-defined power-law mid-IR SEDs of Arp 220 and Mrk 231 shown in Fig. 2.

It is not always necessary to relate the SED f and luminosity L of a galaxy to the mass of dust M_d that it contains; this can of worms can remain closed by normalizing f in a self-consistent way. However, if a dust mass is required, perhaps in order to estimate the metal content of the ISM, and so provide information about the integrated star-formation activity in the galaxy at earlier times (Hughes et al., 1997; Omont et al., 2001), then it is conventional to define a frequency-dependent mass-absorption coefficient (Draine and Lee, 1984; with units of m² kg^-1), which is proportional to . is the `effective area' for blackbody emission by a certain mass of dust,

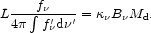(2)

Values of at a conventional frequency of around 1 mm are in the range 0.04-0.15 m² kg^-1 (Hughes, 1996). Recent comparisons of optical extinction and submm emission from partially resolved edge-on spiral galaxies have tended to give values of 0.05-0.4 m² kg^-1 (see Fig. 4 of Alton et al., 2001). Domingue et al. (1999) derive 0.09 m² kg^-1 from similar far-IR, optical and submm data. Dunne et al. (2000) adopt a value of 0.077 m² kg^-1. Note that there is at least a factor of 3 uncertainty in these conversion factors.

An alternative dimensionless function Q (Hildebrand, 1983) is sometimes used, which includes information about the mass/volume and surface area of a typical grain. If grains are assumed to be spherical (a big if), with bulk density , radius a, and an emissive cross section a², then = 3Q / 4a . Q B is the effective emissivity function describing the energy flux from unit area of the dust grain surface. However, dust grains are more likely to be irregular in shape, possibly colloidal or in the form of whiskers. In that case, the emissivity per unit mass would be increased, and the dust mass associated with a fixed luminosity would be overestimated.

This geometrical uncertainty will inevitably result in uncertainty about the mass of dust. Hence, dust masses quoted in papers must be treated with caution, and may be best used as a comparative measure to distinguish galaxies. In general, we will avoid quoting dust masses, as this is unlikely to provide a reliable physical measure of the properties of galaxies until detailed resolved images are available, which is likely to require observations with the ALMA interferometer. This will be a recurring theme: observations with excellent sensitivity and spatial resolution using a large interferometer will resolve many of the questions raised throughout the paper.

Working from submm data, it is also difficult to assess the dust mass of a galaxy, even subject to the caveats above, without knowing its dust temperature. In the Rayleigh-Jeans spectral regime, the flux density from a galaxy S ²⁺ M_d T_d. If T_d is uncertain to within a factor, then M_d is uncertain to within the same factor. The dust mass is at least easier to estimate from a single long-wavelength observation than the luminosity L. As L M_d T_d⁴⁺, or equivalently L S T_d³⁺, an uncertainty in T_d corresponds to a proportionally much larger uncertainty in the inferred value of L.

However, even if the dust mass can be determined reliably at low redshifts, it remains unclear whether the same procedure can be applied to determine the dust mass in more luminous and more distant systems. In order to determine the dust properties of high-redshift galaxies, data of the same quality that has been obtained for nearby galaxies is required. High-frequency submm/far-IR observations are necessary to provide information about the rest-frame frequency of the peak of the SED for a high-redshift galaxy.

Given the current lack of resolved images of distant galaxies in the submm and far-IR wavebands, it is important to neither over-parametrize the descriptions nor overinterpret the results of observations of their SEDs. When spatially-resolved, high-spectral resolution images are available, building on existing interferometric images of low-redshift dusty galaxies (Downes and Solomon, 1998; Sakamoto et al., 1999; Wilson et al., 2000), it should be possible to study the radiative transfer from sites of intense star formation and AGN in these geometrically complex opaque galaxies (see Ivison et al., 2000a, 2001). Models of the SEDs of dust-enshrouded AGN at different viewing angles have been developed by Granato et al. (1996), while star-forming regions embedded in a disk geometry have been analyzed by Devriendt et al. (1999). More powerful and efficient radiative-transfer codes are being developed (for example Abel et al., 1999), and it should be practical to develop detailed models of the appearance of galaxies with realistic geometries to account for future, high-resolution multi-band submm images.

At present, we prefer to use a few simple parameters - , and T_d - to describe the essential features of the SEDs of dusty galaxies. Although such a model can encapsulate only a small part of the true complexity of the astrophysics in a galaxy, it can account for the existing SED data for a wide variety of dusty galaxies. A simple parametrization is preferable to a more baroque, and necessarily at present unconstrained, combination of geometry, dust mass and temperature. In the following section we list plausible values of our SED parameters and discuss the associated degeneracies in fitted values.