3. THE OBSERVED PROPERTIES OF SUBMM-SELECTED GALAXIES

Well over 100 submm-selected galaxies are now known (see Fig. 9), although their redshifts and detailed astrophysical properties are very largely uncertain. The key information available about their properties comes from observations of discrete galaxies made using the SCUBA and MAMBO bolometer array cameras at wavelengths of 450, 850 and 1200 µm. Counts of distant galaxies at far-IR wavelengths of 95 and 175 µm have also been measured using the PHOT instrument aboard ISO. Limits to the counts at 2.8 mm have been obtained using the Berkeley-Illinois-Maryland Association (BIMA) mm-wave interferometer. The results of all the relevant observations are compiled in Figs. 9 and 10. Information is also available about the population of mid-IR 15-µm sources using the CAM instrument aboard ISO (Altieri et al., 1999; Elbaz et al., 1999): see Fig. 22.

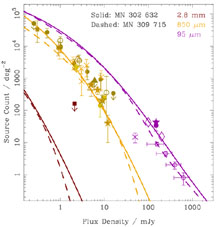Figure 9. A summary of count data from several mm, submm and far-IR surveys. The overplotted curves are derived in models that provide good fits to the compilation of data, and are updated from the results in the listed MNRAS papers (Blain et al., 1999b, c). Identical symbols represent post-1999 data from the same source. The errors are shown as 1 values unless stated. The 2.8 mm data (square) is from Wilner and Wright (1997). At 850 µm, in order of increasing flux (less than 15 mJy), data is from Blain et al. (1999a), Cowie et al. (2002) with 90% confidence limits; Hughes et al. (1998), Chapman et al. (2001b), Barger et al. (1999a, 1998), Smail et al. (1997), Eales et al. (1999, 2000) consistent with the increased area reported by Webb et al. (2002a), Borys et al. (2002), Barger et al. (2000) and Scott et al. (2002). The data points between about 2 and 10 mJy are consistent with a steep integral source count N( > S) S, with a power-law index - 1.6. The counts at brighter flux densities are likely to steepen considerably; note that the counts must turn over at fainter flux densities to have < - 1 to avoid the background radiation intensity diverging. At 95 µm, the data is from Juvela et al. (2000), Kawara et al. (1998), Matsuhara et al. (2000), Serjeant et al. (2001) and Linden-Vornle et al. (2000).

Measurements of the observed intensity of background radiation from the radio to far-UV wavebands are shown in Fig. 11. The background measurements include lower limits obtained by summing over the observed counts plotted in Figs. 9 and 10 the deepest counts at 850 and 15 µm come from surveys made in fields magnified by gravitational lensing clusters. Surface brightness conservation in the lensing process ensures that the mean background intensity in the direction of a lens should be the same as that in a blank field.

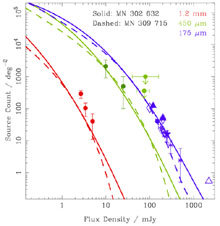Figure 10. Counterpart to Fig. 9 for three other observing bands. The data at 1.2 mm (circles at flux densities less than 10 mJy) are from Bertoldi et al. (2001), Carilli et al. (2000) and Carilli (2001). The data at 450 µm (circles at 10-50 mJy) are from Smail et al. (2002), with limits from Smail et al. (1997) and Barger et al. (1998). The data at 175 µm (100 mJy) are from Kawara et al. (1998), Puget et al. (1999), Matsuhara et al. (2000), Juvela et al. (2000), Dole et al. (2001) and Stickel et al. (1998).

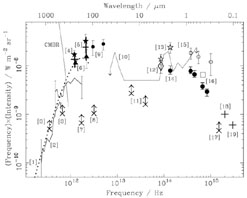Figure 11. The observed intensity of cosmic background radiation between the radio and far-UV wavebands. The great majority of the background energy density in the Universe derived from sources other than the CMB is represented in this figure. Almost all of the rest appears in the X-ray waveband. Some significant uncertainty remains, but the combination of measurements and limits indicates that a comparable amount of energy is incorporated in the far-IR background, which peaks at a wavelength of about 200 µm, and in the near-IR/optical background, which peaks at a wavelength between 1 and 2 µm. The data originates from a wide range of sources: 1. Fixsen et al. (1998); 2. Puget et al. (1996); 3. Blain et al. (1999a); 4. Schlegel et al. (1998); 5. Hauser et al. (1998); 6. Lagache et al. (2000a) see also Kiss et al. (2001); 7. Puget et al. (1999); 8. Kawara et al. (1998); 9. Finkbeiner et al. (2000); 10. Stanev and Franceschini (1998); 11. Altieri et al. (1999); 12. Dwek and Arendt (1998); 13. Wright and Johnson (2002); 14. Pozzetti et al. (1998); 15. Bernstein (1999) and Bernstein et al. (2002); 16. Toller et al. (1987); 17. Armand et al. (1994); 18. Lampton et al. (1990); and 19. Murthy et al. (1999). For a detailed review of cosmic IR backgrounds see Hauser and Dwek (2001). Note that Lagache et al. (2000a, b) claim that the Finkbeiner et al. points (9) could be affected by diffuse zodiacal emission. Where multiple results are available in the literature the most sensitive result is quoted.

From the properties of the counts and backgrounds alone, without any details of the individual galaxies involved, it is possible to infer important details about the population of distant dust-enshrouded galaxies.

The significant surface density of the faint SCUBA and MAMBO galaxies, when coupled to plausible SEDs (Blain et al., 1999b; Trentham et al., 1999; Dunne et al., 2000), clearly indicates that the luminosity function of distant dusty submm galaxies is much greater than that of low-redshift IRAS galaxies (Saunders et al., 1990; Soifer and Neugebauer, 1991), and undergoes very strong evolution. An extrapolation of the low-redshift luminosity function without evolution predicts a surface density of galaxies brighter than 5 mJy at 850 µm of only about 0.25 deg^-2, as compared with the observed density of several 100 deg^-2 (Fig. 9). Because of the flat flux density-redshift relation in the submm shown in Fig. 4, a 5-mJy SCUBA galaxy at any moderate or high redshift (z > 0.5) has a luminosity greater than about 8 × 10¹² L. Immediately, this tells us that the comoving density of high-redshift galaxies with luminosities in excess of about 10¹³ L is 400 times greater than at z = 0. We stress that the submm K correction ensures that the redshift has little effect on the results: the count would be approximately the same whether the population is concentrated at z 1 or extends from z 2 to 10.

This estimate is subject only to an uncertainty in the dust temperature, which is assumed to be about 40 K. Even if the dust temperature of some of the galaxies is as low as the 20 K found for low-redshift spiral galaxies, then their luminosity is still about 8 × 10¹¹ L, considerably greater than the several 10¹⁰ L expected for typical spiral galaxies. This issue can be addressed by taking into account both the observed background spectrum and the counts at different wavelengths.

The submm-wave background radiation spectrum can also be exploited to provide information about the form of evolution of the luminosity function. The submm-wave background, measured directly using COBE-FIRAS (Puget et al., 1996; Hauser et al., 1998; Schlegel et al., 1998), reasonably exceeds the sum of the measured flux densities of discrete galaxies detected in SCUBA surveys (Smail et al., 1997, 2002; Blain et al., 1999a). However, the submm background makes up only a small fraction of the total energy density in the far-IR background, which peaks at a wavelength of about 200 µm and is generated by galaxies at redshift z ~ 1. The relatively flat source SEDs and the rate of change of the cosmic volume element at this redshift conspire to generate most of the background light, just as in the radio, X-ray, optical and near-IR wavebands. The mm and submm background radiation is unique in originating at a higher redshift. Very little of the background is expected to be generated at z < 1, and so it is an important signature of high-redshift galaxy formation. Despite representing only a small fraction of the total energy density in the cosmic background radiation, the mm-wave background is one of the cleanest measures of activity in the distant Universe.

There are significant consequences for the evolution of galaxies at high redshifts due to the observed smooth power-law form of the background spectrum, I ^2.64, for < 500 GHz (Fixsen et al., 1998), which originates at moderate to high redshifts, on account of the submm-wave K correction. The shape of the background radiation spectrum at frequencies greater than about 100 GHz can be approximated quite accurately by associating an evolving comoving volume emissivity (^L in units of W m^-3) with an SED that peaks at a single frequency ₀, so that ^L(z) ( - ₀) (Blain and Longair, 1993b), and then integrating over cosmic volume over a fixed angle on the sky. If the SED, via ₀, is assumed not to evolve strongly with redshift - there is no clear evidence that it does - then in order to reproduce the observed slope of the mm/submm background spectrum, ^L(z) (1 + z) ^-1.1 is required for z >> 1, and so the comoving luminosity density of dust-enshrouded galaxies must decline at large redshifts. If it did not decline, then the background spectrum measured by COBE would be too flat, with too much energy appearing at long wavelengths. This argument has been made using Monte-Carlo simulations of ^L(z) by Gispert et al. (2000). A similar set of simulations have been carried out by Eales et al. (2000), taking into account the observed background radiation spectrum, counts and inferred redshift distribution of submm-selected galaxies.

An approximately equal fraction of the cosmic background radiation energy density emerges in the near-IR/optical and far-IR wavebands (Fig. 11). Because dusty galaxies do not dominate the total volume emissivity at low redshifts (Sanders, 1999; Yun et al., 2001), then the volume emissivity of dusty galaxies must increase by a factor of at least 10, matching the significant evolution of the population of galaxies observed in the optical waveband at z < 1 (Lilly et al., 1996), to avoid the intensity of the far-IR background radiation being significantly less than observed. Only a very small fraction of the total far-IR luminosity from all low-redshift galaxies comes from galaxies more luminous than 10¹² L, yet as discussed above in the context of the submm-wave counts, these luminous galaxies are much more numerous at high redshifts, by a factor of several hundred. These twin constraints demand that the form of evolution of the luminosity function of dusty galaxies cannot be pure density evolution, a simple increase in the comoving space density of all far-IR-luminous galaxies. If the counts were to be reproduced correctly in such a model, then the associated background radiation spectrum would be much greater than observed. A form of evolution similar to pure luminosity evolution, in which the comoving space density of galaxies remains constant, but the value of L^*, the luminosity that corresponds to the knee in the luminosity function, increases - in this case by a factor of order 20 - is consistent with both the submm-wave counts and background intensity.

By a more rigorous process, taking into account all available information, including the need to normalize the results to the observed low-redshift population of dust-enshrouded galaxies from the IRAS luminosity function and the populations of galaxies observed by ISO at z 1, the evolution of the luminosity density ^L can be constrained. The results have been discussed by Blain et al. (1999b, c), as updated in Smail et al. (2002), and by Eales et al. (2000). They are discussed further in Section 5 below.