7. HALO MASSES AND GALAXY MASS-TO-LIGHT RATIOS

Although it ought to be straightforward and even easy to compare the halo masses and galaxy mass-to-light ratios that are obtained from different studies, in practice it is rather like comparing persimmons to tomatoes; i.e., they are vaguely similar on the inside and outside, but they are definitely not interchangeable. The fundamental problem is that it is simply not possible to measure the "total" mass of a galaxy halo (since it is not possible to say where such a halo "ends") and, hence, all halo masses are simply masses that are contained within some physical radius of the center of the halo. Along those same lines, and given that velocity dispersion profiles of NFW halos decrease with radius, if one wants to compare the results of two investigations which have measured a velocity dispersion averaged over some large scale, it is important that those scales be identical. That is, suppose a single measurement of _v is made by averaging over scales r < 100 h^-1 kpc in one study and a single measurement of _v is made by averaging over scales r < 200 h^-1 kpc in another. If the second measurement of _v is lower than the first by some significant amount, that does not necessarily mean that the values are in disagreement. They would be in disagreement if both halos were isothermal spheres, but if the halos are NFW objects, then it is only to be expected that the second measurement would be lower than the first.

A more subtle problem is the definition of the "virial radius" in the context of NFW halos. While r₂₀₀ was originally proposed as the radius at which the interior mass density is 200 times the critical mass density (e.g., [5], [6], [7]), it is not at all uncommon to find that investigators who have fit NFW models to their data have defined the virial radius as the radius at which the interior mass density is 200 times the mean mass density of the universe. Therefore, what is meant by a "virial mass" in the context of an NFW fit to data can (and does) vary from investigation to investigation, and a certain amount of care has to be taken when comparing such results. Despite the difficulties of comparing the conclusions of different studies, I will forge ahead because it is becoming clear that a consistent picture really is emerging on the topic of the masses of the halos of field galaxies, and their corresponding mass-to-light ratios. The weak lensing studies yield results that are by and large consistent with each other, and the dynamical studies seem to be in general agreement with the trends in the weak lensing data: the halos have masses that are consistent with expectations for galaxy-sized halos in CDM, and there are real, physical differences between halos surrounding (i) early-type and late-type galaxies and (ii) high-luminosity and low-luminosity galaxies.

7.1. M and M / L from Galaxy-Galaxy Lensing

In the case of galaxy-galaxy lensing, it is not possible at the moment to discriminate between shear profiles that are caused by NFW versus isothermal galaxy halos. Therefore, investigators will often choose one or the other to constrain the properties of the halos that are producing the lensing signal. In the case of isothermal sphere halos, the velocity dispersions of the lens galaxies used to model the observed signal are often chosen to scale as in eqn. (19) above, (_v / _v^*) = (L / L^*), where again _v is the velocity dispersion of a halo that contains a galaxy of luminosity L, and _v^* is the velocity dispersion of the halo of an L^* galaxy. Hoekstra et al. [48] used this approach with their RCS data, as did Kleinheinrich et al. [60] with their COMBO-17 data. When all lenses and sources were used in the investigations, and when the lensing signal was averaged over an identical scale (r 350 h^-1 kpc), both the RCS and COMBO-17 results are in very good agreement with each other. In particular, Hoekstra et al. [48] find _v^* = 136 ± 8 km sec^-1 for an adopted value of = 0.3, and Kleinheinrich et al. [60] find _v^* = 138⁺¹⁸_-24 and = 0.34^+0.18_-0.12. Further, Kleinheinrich et al. [60] find that there are clear differences in the halos surrounding "blue" galaxies (rest frame colors of (U - V) 1.15 - 0.31z - 0.08[M_V -5 log h + 20]) and those surrounding "red" galaxies (the remainder of the sample). That is, the red COMBO-17 lens galaxies have a higher velocity dispersion than the blue COMBO-17 lens galaxies, but both have a similar value of the index above. See Figure 8.

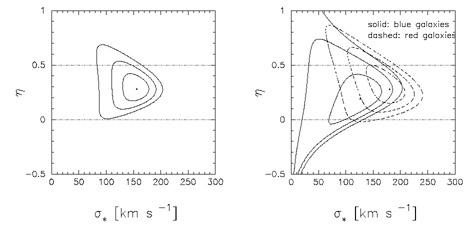Figure 8. Isothermal sphere models for the galaxy-galaxy data from COMBO-17 [60]. Joint constraints (1, 2, and 3) on the velocity dispersion, v*, of the halos of L* galaxies and the index of the Tully-Fisher/Faber-Jackson relation, . Here the weak lensing signal has been averaged over scales rp 150 h-1 kpc. Left panels: all lenses, v* = 156+18-18 km sec-1, = 0.28+0.12-0.09. Right panels: red lenses (2579 galaxies, *v,red = 180+24-30 km sec-1) Left panels: blue lenses (9898 galaxies, *v,blue = 126+30-36 km sec-1). Figure kindly provided by Martina Kleinheinrich.

In addition, Guzik & Seljak [16], Hoekstra et al. [48], and Kleinheinrich et al. [60] have all used NFW halos to model their lens galaxies, and all find very reasonable fits to their lensing signals. Further, the derived values of the NFW virial masses of the halos of L^* galaxies are in quite good agreement amongst these studies when they are determined in similar band passes (e.g., r) and with identical definitions of the virial radius [60]: M_vir^* = 8.96 ± 1.59 × 10¹¹ h^-1 M [16], M_vir^* = 8.4 ± 0.7 × 10¹¹ h^-1 M [48], and M_vir^* = 7.8^+3.5_-2.7 × 10¹¹ h^-1 M [60]. These are also in remarkably good agreement with the virial mass implied for the halos of L^* galaxies by the dynamical analysis of Prada et al. [27] (e.g., M_vir^* ~ 10 × 10¹¹ h^-1 M). Shown in Figure 9 are 1, 2 and 3 confidence limits on a joint-parameter fit of the circular velocity at r₂₀₀, V₂₀₀, and scale radius, r_s, for the lenses in the RCS data [48]. Note that in the analysis of the RCS data, V₂₀₀ and r_s were allowed to vary freely, while, to within some scatter, these parameters are strongly correlated in the NFW theory (i.e., the NFW model is in essence specified by a single parameter). The dashed line in Figure 9 therefore shows the prediction for a strict adherence to the NFW theory (i.e., V₂₀₀ and r_s are correlated appropriately), and the fact that the theoretical NFW line passes so well through the contours gives a certain amount of confidence that the NFW model is a very good fit to the data. Kleinheinrich et al. [60] find good fits of the NFW model to their data and, moreover, find that both the virial radii of the halos and the parameter are dependent upon the rest frame colors of the galaxies, with red galaxies having a somewhat larger virial radius (and, hence, larger virial mass) than blue galaxies. See Figure 10. Here is defined not as in eqn. (19), since the velocity dispersion is a function of projected radius in the NFW model, but rather it is defined as:

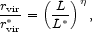(20)

in analogy to the Tully-Fisher and Faber-Jackson relations (see [60]). In this case, r_vir^* is the virial radius of the halo of an L^* galaxy, defined at 200 times the mean mass density of the universe. The variation of with galaxy color and its implications for the mass-to-light ratios of the galaxies will be discussed below.

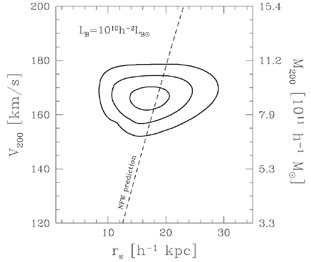Figure 9. Constraints on the circular velocity at r = r200 and the scale radius, rs, for lenses in the RCS that have been modeled as having NFW-type halos [48]. Formally, the best-fitting values of the circular velocity, scale radius and virial mass are: V200 = 162 ± 8 km sec-1, rs = 16.2+3.6-2.9 h-1 kpc, and M200 = 8.4 ± 1.1 × 1011 h-1 M. Here r200 is defined as the radius at which the mean interior mass density of the halo is equal to 200c. The dashed line shows the predictions of the NFW theory, in which V200 and r200 are not independent parameters. Figure kindly provided by Henk Hoekstra.

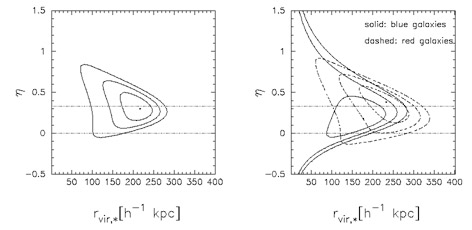Figure 10. NFW halo models of the galaxy-galaxy lensing data from COMBO-17 [60]. Joint constraints (1, 2, and 3) on and the virial radii of the halos of L* galaxies are shown. Left panel: all lenses, = 0.30+0.16-0.12, rvir* = 217+24-32 h-1 kpc. Right panel: red lenses (2579 galaxies, = 0.38+0.16-0.20, rvir* = 233+48-48 h-1 kpc) versus blue lenses (9898 galaxies, = 0.18+0.16-0.16, rvir* = 177+40-56 h-1 kpc). Figure kindly provided by Martina Kleinheinrich.

A particularly detailed study of the masses of lensing galaxies as a function of their color was carried out by Guzik & Seljak [16] for ~ 3.5 × 10⁴ lenses and ~ 3.6 × 10⁶ sources in the SDSS. All of the lens galaxies have spectroscopic redshifts in this case, and all of the halos were modeled as NFW objects in the context of the "halo model". In all 5 of the SDSS band passes, Guzik & Seljak [16] find that the virial masses of L^* ellipticals exceed those of L^* spirals though, unsurprisingly, the amount by which the masses of the ellipticals exceeds those of the spirals is a strong function of the band pass. In the redder bands, the masses of the ellipticals exceed those of the spirals by a factor of ~ 2 to ~ 2.5, while in g' the difference is a factor of ~ 6 and in u' the difference is close to an order of magnitude. Although it is difficult to make direct comparisons between the two studies (because of the differing definitions of the virial radius and the different definitions of the subsamples of galaxies), there is good general agreement between the results of Guzik & Seljak [16] and Kleinheinrich et al. [60]: when the galaxy-galaxy lensing signal is detected red band passes (e.g., R, r') and the lenses are modeled as NFW objects, the virial masses of red/early-type galaxies exceed those of blue/late-type galaxies by a factor of order 2.

In addition to the halos of early-type lenses having more mass than those of late-type lenses, the weak lensing work of Sheldon et al. [42] indicates that, again, in all 5 SDSS band passes, the projected excess surface mass density increases with the luminosity of the lens. Sheldon et al. [42] separated their ~ 1.27 × 10⁵ lenses into 3 magnitude bins (high, middle, and low luminosity), and the magnitude cuts differ for the different band passes. (See Table 2 of Sheldon et al. [42] for a complete list of the magnitude cuts as a function of band pass.) In the case of the r' data, the "high" luminosity galaxies have a mean absolute magnitude of -22.5, the "middle" luminosity galaxies have a mean absolute magnitude of -21.9, and the "low" luminosity galaxies have a mean absolute magnitude of -20.5. These mean luminosities correspond roughly to 4.5L^* ("high"), 2.7L^* ("middle") and 0.8L^* ("low") in the r' band. In all cases, (r_p) for the "high" luminosity galaxies exceeds that of the "medium" and "low" luminosity galaxies, and for r_p 1 h^-1 Mpc, the difference corresponds to an approximately constant multiplicative factor. Specifically at r_p ~ 100 h^-1 Mpc, however, for the high luminosity lenses in Sheldon et al. [42] exceeds that for the low luminosity lenses by a factors of ~ 3 in u', ~ 5 in g', ~ 5 in r', ~ 7 in i', and ~ 7 in z' (e.g., Figure 14 of Sheldon et al. [42]). Similar trends (i.e., higher projected excess surface mass density for more luminous lenses) were found by Seljak et al. [61] in their galaxy-galaxy lensing analysis of SDSS data.

Lastly, although there is reasonable agreement regarding the relative increase in mass for the halos of early-type lens galaxies versus late-type lens galaxies at fixed luminosity (i.e., L^*), there is some disagreement over the dependence of the mass-to-light ratio on the luminosity of the host. Specifically, in their redder bands Guzik & Seljak [16] find that the mass-to-light ratio goes as M / L L^0.4±0.2 for L > L^*, suggestive of a mass-to-light ratio that increases with luminosity. Kleinheinrich et al. [60], however, find that M / L for their sample of lenses is more consistent with a constant value: M / L L^{-0.10+0.48_-0.36}. Both Guzik & Seljak [16] and Kleinheinrich et al. [60] agree, however, that the mass-to-light ratio of red/early-type L^* lens galaxies exceeds that of blue/late-type L^* lens galaxies by a factor of ~ 2 to ~ 2.5 in the redder bands.

7.2. M and M / L from Satellite Dynamics

In the 1990's, Zaritsky et al. [20] and Zaritsky & White [98] used the velocity differences between a small number of isolated spiral galaxies and their satellites to show that the halos of the spirals were massive and extended to large radii: M(150 h^-1 kpc) ~ 1 to 2 × 10¹²h^-1 M. Moreover, Zaritsky et al. [20] found a somewhat curious result: the velocity difference between their 115 satellites and 69 hosts was independent of the inclination corrected H-I line width of the host and was, therefore, independent of the luminosity of the host (through, e.g., the Tully-Fisher relation). At fixed large radius, then, this would imply that M / L for the spiral hosts decreased as M / L L^-1.

More recent investigations of halo masses and corresponding mass-to-light ratios from satellite dynamics have led to rather a large assortment of conclusions. McKay et al. [65] and Brainerd & Specian [66] used the dynamics of the satellites of SDSS galaxies and 2dFGRS galaxies, respectively, to constrain the dynamical masses of the halos of the host galaxies interior to a radius of r = 260 h^-1 kpc. Both used an isothermal mass estimator of the form

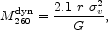(21)

where _v is the line-of-sight velocity dispersion. Both felt this assumption was justified because both found that their velocity dispersion profiles were consistent with a constant value. In the case of McKay et al. [65], however, no correction for an increasing number of interlopers with projected radius was made and this may have led to an incorrect conclusion that _v(r_p) was independent of r_p. In the case of Brainerd & Specian [66], the increasing number of interlopers at large r_p was taken into account, but only galaxies from the 100k data release of the 2dFGRS were used (i.e., roughly half as many galaxies as in the full data release), and although _v(r_p) was consistent with a constant value in their data, the later analysis by Brainerd [67] showed that this was simply due to the rather large error bars in Brainerd & Specian [66]. This being the case, the mass-to-light ratios published by these two studies are suspect at some level, but it is unclear at the moment just how suspect they may actually be. That is, while it is true that the velocity dispersion profile of NFW halos decreases with radius, the fall-off in _v(r_p) is not particularly sharp and it is not obvious how badly isothermal mass estimates of the form in eqn. (21), which are based on an average value of _v, will compare to proper NFW mass estimates.

Formally, McKay et al. [65] found that in all 5 SDSS band passes, M₂₆₀^dyn / L was roughly constant for L > L^*, and that the value of M₂₆₀^dyn / L was a strong function of the band pass (being systematically higher in the blue bands than in the red bands). Brainerd & Specian [66] found that for L 2L^*, M₂₆₀^dyn / L was a constant for dynamical analyses that included (i) all 809 hosts in their sample and (ii) 159 hosts that had been visually classified as early-type (E/S0). However, much like the results of Zartisky et al. [20], Brainerd & Specian [66] found that M₂₆₀^dyn / L decreased as M₂₆₀^dyn / L L^-1 for 243 hosts that had been visually classified as spirals. This latter result remains puzzling, and is certainly in need of further investigation with larger data sets.

In their analysis of the dynamics of the satellites of SDSS host galaxies, Prada et al. [27] found that the velocity dispersion of the satellites scaled with host luminosity as _v L^0.3 (i.e., in good agreement with the local B-band Tully-Fisher relationship [99]) for satellites with projected radii r_p < 120 kpc. (Recall, too, that in this study _v(r_p) was specifically corrected for the increase in interlopers at large r_p.) In addition, Prada et al. [27] found that for satellites at large projected radius, 250 kpc < r_p < 350 kpc, the velocity dispersion scaled with luminosity as _v L^0.5 (i.e., steeper than expected from the Tully-Fisher relation). See Figure 11.

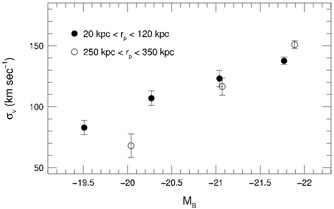Figure 11. Dependence of satellite velocity dispersion on host absolute magnitude for SDSS galaxies [27]. Filled circles: v computed using satellites with 20 kpc rp 120 kpc. Open circles: v computed using satellites with 250 kpc rp 350 kpc. For small projected radii the velocity dispersion scales as v L0.3, in good agreement with the local B-band Tully-Fisher relationship. For large projected radii v L0.5. Here h = 0.7 has been adopted.

Similar to Prada et al. [27], Brainerd [67] also computed the dependence of the small-scale velocity dispersion of satellites on host luminosity. See Figure 12. Like Prada et al. [27], Brainerd [67] corrected for the fact that the interloper fraction is an increasing function of projected radius and overall, she found excellent agreement between the velocity dispersions of satellites with projected radii r_p 120 kpc in the 2dFGRS and GIF simulations. The velocity dispersions of the 2dFGRS satellites were, however, seen to scale with host luminosity as _v L_bJ^0.45±0.10, which is only marginally consistent with the results of Prada et al. [27] and the local B-band Tully-Fisher relationship.

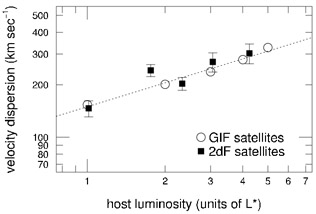Figure 12. Dependence of satellite velocity dispersion on host luminosity for satellites with projected radii rp 120 kpc in both the 2dFGRS and the flat, -dominated GIF simulation [67]. Dotted line shows v L0.45.

Prada et al. [27] have shown (e.g., their Figure 12) that the dependence of the line of sight velocity dispersion on the virial mass of NFW halos scales as _v M_vir^0.38 for the case that _v is computed as an average over scales 20 kpc r_p 100 kpc, and that _v M_vir^0.50 for the case that _v is computed at r_p ~ 350 kpc. Combining this with their results for the dependence of _v on L at different scales leads to the conclusion that on scales r_p 120 kpc, M_vir / L L^-0.2 while on scales r_p ~ 300 kpc, M_vir / L is a constant. Similarly, if the halos of the 2dFGRS galaxies studied by Brainerd [67] are assumed to be NFW objects, the implication is that M_vir / L L^0.2+0.3_-0.1 for the 2dFGRS hosts (again, computed on scales r_p 120 kpc).

While it certainly cannot be said that there is a consensus from weak lensing and satellite dynamics as to the exact dependence of the galaxy mass-to-light ratio on L, it does seem to be the case that all of these studies point towards a dependence of M_vir / L on L that is, at most, rather weak. That is, with the notable exception of the Brainerd & Specian [66] result for late-type galaxies, all of the recent determinations of M / L for L L^* find that, to within 2, M/L is independent of L. In addition, when the weak lenses and host galaxies are each modeled as NFW objects, a fairly consistent value of the average virial mass of the halos of L^* galaxies is found: ~ (8 - 10) × 10¹¹ h^-1 M. Further, it seems to be clear that both weak lensing and satellite dynamics indicate that the masses of the halos of early-type galaxies are larger than that of late-type galaxies, and that at fixed luminosity the mass-to-light ratios of early-type galaxies are larger than those of late-type galaxies.