


The evolutionary models described in
Section 15.5 are based on complex
numerical calculations that tend to obscure connections between
important features in the data and the calculated radio luminosity
functions, redshift distributions, etc. In contrast,
von Hoerner (1973)
demonstrated with analytic approximations the
importance of the broad visibility function
 (Equation
15.14) to
the radio Hubble relation and to the form of the source count. In a
uniformly filled, static Euclidean universe, the visibility function has
no effect on the form of the source count
(Equation 15.16) or the Hubble relation. The visibility function is
important only if its width,
(Equation
15.14) to
the radio Hubble relation and to the form of the source count. In a
uniformly filled, static Euclidean universe, the visibility function has
no effect on the form of the source count
(Equation 15.16) or the Hubble relation. The visibility function is
important only if its width,
 log L, is
greater than twice the redshift range,
log L, is
greater than twice the redshift range,
 log z,
containing most
radio sources. Thus, the actual distribution of extragalactic radio
sources in distance (lookback time) is so nonuniform that features in
the source counts should not be
interpreted as perturbations from a static Euclidean count. A much
better starting model for the radio universe is actually a hollow shell
centered on the observer! This "shell model" reproduces many features of
the data almost as well as the more
elaborate models and clearly shows how they are related to the
distribution of sources in space.
log z,
containing most
radio sources. Thus, the actual distribution of extragalactic radio
sources in distance (lookback time) is so nonuniform that features in
the source counts should not be
interpreted as perturbations from a static Euclidean count. A much
better starting model for the radio universe is actually a hollow shell
centered on the observer! This "shell model" reproduces many features of
the data almost as well as the more
elaborate models and clearly shows how they are related to the
distribution of sources in space.
For sources with average spectral index
< > the
relation
> the
relation
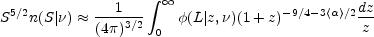 |
(15.30) |
is a good approximation to the exact Equations (15.20) and (15.21) for
all 0 

 2, z < 5
(Condon 1984a).
If most radio sources are confined to a thin shell of thickness
2, z < 5
(Condon 1984a).
If most radio sources are confined to a thin shell of thickness
 zs at redshift zs,
zs at redshift zs,
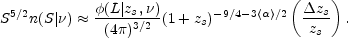 |
(15.31) |
We assume translation evolution so
 m(L| z,
m(L| z,
 ) = g(z)
) = g(z)
 m[L / f (z)| z = 0,
m[L / f (z)| z = 0,
 ]. Let
gs
]. Let
gs  g(zs) be the amount of density evolution and
fs
g(zs) be the amount of density evolution and
fs  f (zs) be the amount of luminosity
evolution at the shell redshift. Then,
log[
f (zs) be the amount of luminosity
evolution at the shell redshift. Then,
log[ (L |
zs,
(L |
zs,
 )] =
log[
)] =
log[ (L /
fs| z = O,
(L /
fs| z = O,
 )] + 3
log(fs) / 2 + log(gs) and
)] + 3
log(fs) / 2 + log(gs) and
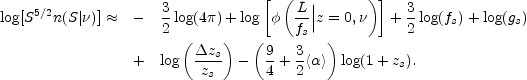 |
(15.32) |
The redshift distribution of sources stronger than S = 2 at
 = 1.4 GHz
(Figure 15.9) suggests
zs
= 1.4 GHz
(Figure 15.9) suggests
zs
 0.8 and (
0.8 and ( zs / zs)
zs / zs)
 1 ; the
spectral-index distribution
[Figure 15.7(b)] gives
<
1 ; the
spectral-index distribution
[Figure 15.7(b)] gives
< >
>
 0.7. Substituting
these quantities yields the following
expression relating the weighted source counts, the local visibility
function, and the evolution parameters at the shell redshift:
0.7. Substituting
these quantities yields the following
expression relating the weighted source counts, the local visibility
function, and the evolution parameters at the shell redshift:
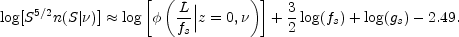 |
(15.33) |
The values of fs and gs that satisfy
Equation (15.33) can be found graphically
by superimposing the observed source counts and local visibility
functions, as shown in Figure 15.17. For
sources with zm
 0.8 and
0.8 and

 0.7,
log[L(W Hz-1)] - log[S(Jy)]
0.7,
log[L(W Hz-1)] - log[S(Jy)]
 26.9. Since the best
fit of the local visibility function to the source counts occurs at
log[L(W Hz-1)] - log[S(Jy)]
26.9. Since the best
fit of the local visibility function to the source counts occurs at
log[L(W Hz-1)] - log[S(Jy)]
 25.7
(Figure 15.17), we require
luminosity evolution in the amount log(fs)
25.7
(Figure 15.17), we require
luminosity evolution in the amount log(fs)
 26.9 - 25.7 =
1.2. This fit also implies
log[S5/2 n(S |
26.9 - 25.7 =
1.2. This fit also implies
log[S5/2 n(S |
 = 1.4 GHz)]
= 1.4 GHz)]
 log[
log[ (L
| z = 0,
(L
| z = 0,  = 1.4 GHz)] -
0.65, resulting in log(gs)
= 1.4 GHz)] -
0.65, resulting in log(gs)
 0.0 (no density
evolution). With these evolution parameters, the weighted
source count predicted by the shell model corresponds exactly to the
local visibility function plotted as the solid line in
Figure 15.17. The
model actually reproduces the entire observed source count from
S
0.0 (no density
evolution). With these evolution parameters, the weighted
source count predicted by the shell model corresponds exactly to the
local visibility function plotted as the solid line in
Figure 15.17. The
model actually reproduces the entire observed source count from
S  10µJy to
S
10µJy to
S  10 Ky.
10 Ky.
Since the shell model ignores local sources, it must fail at the highest
flux densities - the regime in which a nonevolving model is more
appropriate. What is surprising is that the transition flux density is
so high. An exact calculation based
on the same local luminosity function without evolution yields
log[S5/2 n(S |
 = 1.4 GHz)]
= 1.4 GHz)]
 1.8 at high flux
densities (Figure 15.17), so the shell model
and the nonevolving model predict the same source counts at
S
1.8 at high flux
densities (Figure 15.17), so the shell model
and the nonevolving model predict the same source counts at
S  20
Jy. Thus, the static
Euclidean approximation is reasonably good only for S > 20 Jy
at
20
Jy. Thus, the static
Euclidean approximation is reasonably good only for S > 20 Jy
at  = 1.4 GHz; it applies only
to the small number of sources in the very strongest flux-density bin
plotted in Figure 15.17. It should not be used
to describe features in
the observed counts at lower flux densities. For example, the so-called
"Euclidean" regions in which S5/2 n(S |
= 1.4 GHz; it applies only
to the small number of sources in the very strongest flux-density bin
plotted in Figure 15.17. It should not be used
to describe features in
the observed counts at lower flux densities. For example, the so-called
"Euclidean" regions in which S5/2 n(S |
 = 1.4 GHz) is roughly
constant near log[S(Jy)]
= 1.4 GHz) is roughly
constant near log[S(Jy)]
 0 and log[S(Jy)]
0 and log[S(Jy)]
 - 3 do not indicate
that the sources in these flux-density ranges are
comparatively local - they only correspond to maxima in the visibility
function of sources at
z
- 3 do not indicate
that the sources in these flux-density ranges are
comparatively local - they only correspond to maxima in the visibility
function of sources at
z  zs .
zs .
In the shell model, the median source redshift is
<z> = zs
 0.8 for all S
<< 20 Jy,
in good agreement with the observed redshift distribution of sources
stronger than
S = 2 Jy (Figure 15.9) and
the magnitude distributions of galaxies identified with sources as faint
as S
0.8 for all S
<< 20 Jy,
in good agreement with the observed redshift distribution of sources
stronger than
S = 2 Jy (Figure 15.9) and
the magnitude distributions of galaxies identified with sources as faint
as S  1 mJy
(Windhorst et al. 1984a,
Kron et al. 1985).
Since <z>
is independent of S (no Hubble relation), there is a one-to-one
correspondence between average luminosity and flux density that maps
populations from the local
visibility function to the weighted source count. Two consequences are
as follows. (1) All standard evolutionary models
(Section 15.5.2)
require that the evolution function E(L, z) be
largest at high luminosities. The shell
model reproduces this result (see
Figure 15.1) because the difference
between the weighted source counts
observed and predicted by the nonevolving model are largest at high
flux densities. (2) At any flux-density level, most sources will
lie in a narrow range of luminosities;
observations with that sensitivity look beyond the shell for more
luminous sources and will not reach the shell for less luminous
ones. Deeper surveys do not detect more distant sources, only feebler
ones. Consequently, elliptical galaxies account
for nearly all of the strongest radio sources and spiral galaxies the
faintest. There is a transition region at
S
1 mJy
(Windhorst et al. 1984a,
Kron et al. 1985).
Since <z>
is independent of S (no Hubble relation), there is a one-to-one
correspondence between average luminosity and flux density that maps
populations from the local
visibility function to the weighted source count. Two consequences are
as follows. (1) All standard evolutionary models
(Section 15.5.2)
require that the evolution function E(L, z) be
largest at high luminosities. The shell
model reproduces this result (see
Figure 15.1) because the difference
between the weighted source counts
observed and predicted by the nonevolving model are largest at high
flux densities. (2) At any flux-density level, most sources will
lie in a narrow range of luminosities;
observations with that sensitivity look beyond the shell for more
luminous sources and will not reach the shell for less luminous
ones. Deeper surveys do not detect more distant sources, only feebler
ones. Consequently, elliptical galaxies account
for nearly all of the strongest radio sources and spiral galaxies the
faintest. There is a transition region at
S  1 mJy in which
both populations should be present.
Because the local visibility function is falling rapidly for
luminosities L < 1021
W Hz-1 this model also suggests that the (as yet unobserved)
weighted source count will decline rapidly for flux densities
S < 10-5 Jy. [The widespread belief that nearby
galaxies must eventually dominate the source count and cause its slope
to approach the static Euclidean value is incorrect. Even with no
evolution at all in an expanding universe, the slope of the weighted
source count at low flux densities tends to
approach that of the local visibility function at low luminosities
(about 4/3 rather than zero); and most sources are cosmologically
distant, crowding up against the redshift "cutoff" imposed by the
(1 + z)-9/4-3<
1 mJy in which
both populations should be present.
Because the local visibility function is falling rapidly for
luminosities L < 1021
W Hz-1 this model also suggests that the (as yet unobserved)
weighted source count will decline rapidly for flux densities
S < 10-5 Jy. [The widespread belief that nearby
galaxies must eventually dominate the source count and cause its slope
to approach the static Euclidean value is incorrect. Even with no
evolution at all in an expanding universe, the slope of the weighted
source count at low flux densities tends to
approach that of the local visibility function at low luminosities
(about 4/3 rather than zero); and most sources are cosmologically
distant, crowding up against the redshift "cutoff" imposed by the
(1 + z)-9/4-3< >/2 term in Equation (15.30).]
>/2 term in Equation (15.30).]
Many authors have commented that the relatively narrow peak in the weighted
source counts is difficult to model in terms of the relatively broad
local luminosity function. It is inappropriate to compare these
distributions because they do not have the same dimensions. The weighted
source count S5/2n(S |
 ) should only be
compared with the weighted local luminosity function
) should only be
compared with the weighted local luminosity function
 (L|
z = 0,
(L|
z = 0,
 ); the unweighted
source count n(S |
); the unweighted
source count n(S |
 ) is most appropriately
compared with the unweighted local luminosity function
) is most appropriately
compared with the unweighted local luminosity function
 (L |
z = O,
(L |
z = O,  ).
Figure 15.17 shows that the
weighted source counts and the local visibility function peaks actually
have very similar widths at
).
Figure 15.17 shows that the
weighted source counts and the local visibility function peaks actually
have very similar widths at
 = 1.4 GHz. The only
conclusion that can be drawn from the fact
that the weighted source count peak is not much broader than the local
visibility function peak is that some form of evolution is
restricting the lower end of the redshift range
= 1.4 GHz. The only
conclusion that can be drawn from the fact
that the weighted source count peak is not much broader than the local
visibility function peak is that some form of evolution is
restricting the lower end of the redshift range
 log z in
which most radio sources are found. [The factor
(1 + z)-9/4-3<
log z in
which most radio sources are found. [The factor
(1 + z)-9/4-3< >/2 = (1 + z)-3.3 for
<
>/2 = (1 + z)-3.3 for
< > = 0.7 in
Equation (15.30) is quite effective at
suppressing the contribution of high-redshift sources to the observed
source counts, so the success of the shell model is not strong evidence
that evolution stops or reverses at redshifts higher than
zs.]
> = 0.7 in
Equation (15.30) is quite effective at
suppressing the contribution of high-redshift sources to the observed
source counts, so the success of the shell model is not strong evidence
that evolution stops or reverses at redshifts higher than
zs.]
The very similar forms of the local visibility function and the
weighted source count (Figure 15.17) determined
by the visibility function at
z  0.8 indicate
that the form of the visibility function really does not evolve
significantly; i.e., the "translation evolution" approximation is a good
one. Pure luminosity evolution
works in the shell model, and pure density evolution in a thin shell
would also preserve the form of the local visibility function in the
normalized source counts. The amounts of luminosity and density
evolution actually required to fit the data
are determined by the redshift of the shell, the difference between the
luminosity of the local visibility function peak and the flux density of
the weighted count peak, and the difference between the peak values of
the local visibility function and the
weighted source count, as described above. Pure luminosity evolution
shifts the source-count curve along a line of slope 3/2 in the
{log(S), log[S5/2 n(S)]}-plane, and
pure density evolution shifts it vertically. Thus, only one combination
of luminosity and density evolution can match both zm
and the peak of weighted source count exactly.
0.8 indicate
that the form of the visibility function really does not evolve
significantly; i.e., the "translation evolution" approximation is a good
one. Pure luminosity evolution
works in the shell model, and pure density evolution in a thin shell
would also preserve the form of the local visibility function in the
normalized source counts. The amounts of luminosity and density
evolution actually required to fit the data
are determined by the redshift of the shell, the difference between the
luminosity of the local visibility function peak and the flux density of
the weighted count peak, and the difference between the peak values of
the local visibility function and the
weighted source count, as described above. Pure luminosity evolution
shifts the source-count curve along a line of slope 3/2 in the
{log(S), log[S5/2 n(S)]}-plane, and
pure density evolution shifts it vertically. Thus, only one combination
of luminosity and density evolution can match both zm
and the peak of weighted source count exactly.
The shell model emphasizes the insensitivity of the
< > - S
relation to source size evolution. Since there is no Hubble relation for
S << 20 Jy, evolution of the projected
linear size d with z affects sources of all flux densities
equally. Furthermore, most
sources with S << 20 Jy lie at redshifts within a factor of
two of zs = 0.8, so they are
at very nearly the same angular-size distance if
> - S
relation to source size evolution. Since there is no Hubble relation for
S << 20 Jy, evolution of the projected
linear size d with z affects sources of all flux densities
equally. Furthermore, most
sources with S << 20 Jy lie at redshifts within a factor of
two of zs = 0.8, so they are
at very nearly the same angular-size distance if
 = 1
(Figure 15.15). Thus the
<
= 1
(Figure 15.15). Thus the
< > - S
plot really measures the variation of projected linear size d with
luminosity. The flat region with
<
> - S
plot really measures the variation of projected linear size d with
luminosity. The flat region with
< >
>
 10
arcsec extending from
S
10
arcsec extending from
S  1 mJy to
S
1 mJy to
S  1 Jy indicates
that <d>
1 Jy indicates
that <d>  40
kpc for all luminosities in the
range L
40
kpc for all luminosities in the
range L  1024 to 1027 W Hz-1
at
1024 to 1027 W Hz-1
at  = 1.4 GHz. The sudden
falloff to <
= 1.4 GHz. The sudden
falloff to < > < 3
arcsec below
S
> < 3
arcsec below
S  1 mJy cannot
be caused by evolution; it reveals instead a dramatic decline in linear
size to <d> < 10 kpc among sources less luminous than
L
1 mJy cannot
be caused by evolution; it reveals instead a dramatic decline in linear
size to <d> < 10 kpc among sources less luminous than
L  1024 W Hz-1. Such a decline
is expected if most of the sources contributing to the flattening of
S5/2
n(S |
1024 W Hz-1. Such a decline
is expected if most of the sources contributing to the flattening of
S5/2
n(S |  ) below
S
) below
S  1 mJy at
1 mJy at
 = 1.4 GHz are in the disks of
spiral galaxies.
= 1.4 GHz are in the disks of
spiral galaxies.