12.1.2. The Information in the 21-cm Line
Although in most cases HI is just a tracer component of the makeup of a galaxy, it constitutes an important tool in the study of the structure and dynamics of galaxy evolution. Notable reasons for the popularity of the line as such a tool are the ease of detection and the relative reliability of the column densities and other physical parameters inferred from the line profiles.
The 21-cm line results from a magnetic dipole transition between the two
levels that characterize the ground state of the hydrogen
atom. Depending on whether the electronic and nuclear spin vectors are
parallel or antiparallel, a slightly higher
(triplet) or lower (singlet) hyperfine level is obtained. The
statistical equilibrium between the populations of the singlet and
triplet levels can be expressed by means
of the Boltzmann equation, in which the effective temperature that
regulates the relative populations is referred to as the "spin
temperature," Ts. Several processes
contribute to Ts; the most important, as originally
described
by Field (1959),
are: (i) absorption of and emission stimulated by photons of an existing
radiation field;
(ii) collisions of H atoms with other particles, especially with other H
atoms and with electrons; (iii) "pumping" by Lyman
photons. As an example
of the last process, a H atom in the singlet state of n = 1 can
be excited to the n = 2 state by
a Lyman photon;
subsequent deexcitation to the n = l level
will leave the H atom in the triplet level in a fraction of the
cases. Spontaneous transitions from the triplet
to the singlet level occur with a transition probability
A10 = 2.868 × 10-15 s-1; in
most cases of interest, however, a H atom will not be left alone for as
long as eleven million years, and so Ts is largely
determined by the above-mentioned extrinsic influences.
A cloud of optical depth
and spin temperature
Ts, bathed in a radiation field of temperature
Tr, will yield a brightness temperature
 |
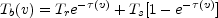(12.1) |
where the optical depth
(v) varies with
velocity v across the line profile. The optical
depth (v) can be
expressed as the ratio of the HI column density to the spin temperature
(see Spitzer 1978).
If one assumes that the gas is optically thin
(i.e., < < 1), the
column density of HI can then be obtained as
 |
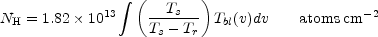(12.2) |
where Tbl(v) is the brightness temperature of
the line profile at velocity v, in cm s-1,
above the continuum or baseline level, and the integral is over the line
profile. Over most of the HI mass of a galactic disk, collisions
determine the population of the
two n = 1 hyperfine levels, and Ts closely
approaches the kinetic temperature of
the gas. Since this is usually much larger than Tr the
term in square brackets in
Equation (12.2) is about unity. In the outer regions of the disks, and
in envelopes of tidal debris after galaxy-galaxy interactions, where gas
densities are low and
collisions rare, Ts will be regulated by the radiation
field at 21 cm and at 1216 Å
(Lyman ). The former
will be dominated by the cosmic background radiation at
2.7 K; in the absence of a sufficient ionizing flux, the term
[Ts / (Ts) - Tr)]
could be significantly larger than 1, and the determination of
NH would
require a knowledge of Ts, which is difficult to obtain.
Watson and Deguchi
(1984)
have shown, however, that the Lyman a flux in intergalactic space may be
large enough that Lyman
pumping regulates the populations of the hyperfine levels and tends to
push Ts to
values well above 2.7 K, thus suggesting that even in very-low-density
clouds outside of disks,
[Ts / (Ts) - Tr)]
remains close to 1. A simple integral across the line then will
give a close estimate of the atomic hydrogen column density. It should
be stressed again that this conclusion rests on the assumption of a
sufficient value for a relatively
uncertain quantity: a pervasive intergalactic ultraviolet flux. If
current estimates of that quantity were to be found too high, column
densities of HI in the outskirts of
galaxies and in diffuse clouds outside of disks would have to be revised.
We address next the validity of the assumption of optical transparency. That assumption is invalid in a number of cases: dense regions of the interstellar medium, whence originate absorption lines, are opaque. The integrated line profile of a galaxy results from the collective emission - and absorption - by all its HI. In order to correctly convert the line integral into a total HI mass, we need to know the fraction of the HI gas in the disk which is found in optically thick regions. That fraction in turn depends on the intrinsic properties of the gas distribution in the galaxy and on the geometrical perspective with which it appears to us. The practical approach to this problem consists in computing column densities in the optically thin approximation and then applying a correction that accounts for self-absorption. The self-absorption correction can be estimated (a) from statistical studies on large samples of galaxies, covering a broad range of disk inclinations and morphological and possibly luminosity class, (b) from HI absorption line studies in our Galaxy, or (c) by modeling the distribution of cold gas in the interstellar medium. A detailed description of these methods is given in Appendix B of Haynes and Giovanelli (1984). The results indicate that when a disk like that of our Galaxy is seen face-on, the assumption of optical transparency leads us to underestimate the column density by a small amount, probably less than five percent. When disks are seen close to edge-on, however, substantial corrections to the column densities and masses inferred using Equation (12.2) become necessary. The corrections appear to be larger for intermediate-type spirals. It is estimated that for the majority of galaxies, such column density corrections amount to factors less than 1.5.
If the distance is known, the total HI mass of a galaxy can be obtained by integrating Equation (12.2) over the effective disk area (i.e., the approximate ellipse obtained by the inclined view of the disk with respect to the line of sight), after correcting for self-absorption. In the case of single-dish observations where the galaxy is unresolved by the beam, Equation (12.2) yields simply
 |
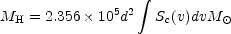(12.3) |
where d is the distance in Mpc and
Sc(v) dv is the
integral, over the line, of the
flux density corrected for self-absorption and other instrumental
biases, with Sc(v) expressed in Jy and v
in km s-1 [see
Roberts (1975)
for details of the derivation of Equation (12.3)].
Standard radio spectroscopy techniques allow for spectral resolutions better than 0.1 km s-1 at 21 cm. Extragalactic observations are however preferentially done with broad bandwidths, covering typically 2000, 4000, or 8000 km s-1; spectral resolutions are then more typically on the order of 5 to 20 km s-1, although they can be much better than that when the signal strength so permits. The fine spectral resolution achievable in the HI line ordinarily allows very precise measurements of radial and rotational velocities of large samples of galaxies. In face-on systems, accurate measurements of the velocity dispersion of the interstellar gas perpendicular to the plane of the disk are possible. In inclined systems, the determination of the disk velocity field allows a detailed study of the large-scale galaxian dynamical characteristics. The maximum rotational velocity, as indicated, for example, by the half-width of a galaxy's integrated line profile, has been found to be a good luminosity indicator, thus providing a powerful method for the determination of extragalactic distances and hence the expansion rate of the universe.
The HI content of a galaxy has been shown to be vulnerable to environmentally driven gas removal mechanisms, and may thus be used to probe the effects of the latter on galaxy evolution. The fragile outer layers of the disk are easily disrupted by close encounters of galaxies, especially of those located in small groups, and HI observations have provided spectacular data on this sort of perturbation. As for the physics of disks, HI observations provide valuable insights on the dynamic and thermal equilibrium of the interstellar medium.
In addition, the combination of large apertures and modern receivers has made the execution of large-scale redshift surveys in the 21-cm line a practical endeavor.
Spiral galaxies within 100 to 200 Mpc are easily detectable in the line with modest investments of telescope time, yielding recessional velocities with errors of only a few km s-1. While optical redshift surveys preferentially favor objects of high central optical surface brightness, galaxies of low optical surface brightness tend to have abundant HI and, at equal apparent magnitude, are more easily detected by radio surveys. For example, while redshifts of galaxies in clusters - where lenticular and elliptical morphologies are most abundant - are usually obtained by optical means, the vast majority of redshifts available for galaxies in the low-density regions of superclusters have been obtained using radio methods.