


12.3.3. The Mass Distribution in Spiral Galaxies
By combining optical photometry data with the mass derived from 21-cm observations via Equation (12.4), we can determine total mass-to-luminosity ratios - although one should note that values thus obtained depend inversely on the assumed distance scale. Arbitrarily choosing some limiting radius, e.g., r25, measured at the blue isophote of 25.0 mag arcsec-2, the integral of Equation (12.4) and the blue luminosity within r25 yield a measure of the global mass-to-light ratio. Using this system, Rubin et al. (1985) find that ratio to be 6.2, 4.5, and 2.6 for Sa, Sb, and Sc galaxies, respectively, with an error on those mean values of about 10%. Since the mass is proportional to r25 Vmax2, and since it is found that, in the blue, the relationship between luminosity and radius is independent of morphological type, the variation in (MT / LB) with type is essentially one of Vmax with type. The mean values of Vmax as a function of type bear out that conclusion. The values of (MT / LB) are virtually constant within a given Hubble type, over a range of several magnitudes. Now, what fraction of the total dynamical mass does the luminous mass constitute? To answer that question, we must first obtain an estimate of the fraction of the total luminous mass represented by LB. Work based on model stellar populations indicates that reasonable values for the ratio between the total mass in all stars and LB are 3.1, 2.0, and 1.0 for Sa, Sb, and Sc types, respectively. Although these numbers are relatively uncertain, they indicate that the ratio of total to luminous mass within the 25-mag arcsec-2, isophote is likely to be on the order of 2 for spirals of all types. As the mass grows more or less linearly and the light fades exponentially, the mass-to-light ratio grows rapidly outwards from r25.
The analysis of rotation curves yields information on the mass distribution as a function of distance from the galactic center, but none whatsoever on the distribution as a function of distance from the plane of the disk. One would like to know which fraction of the total mass resides in the disk and which in the halo, and also how the total mass-to-light ratio of the disk alone varies with radius. In order to answer these questions, it is necessary to measure the characteristics of some tracer of the gravitational potential in the z-direction (i.e., perpendicular to the disk); handily, such is the HI. It is possible to obtain the distribution and the velocity dispersion, in the z-direction, of the galaxian HI. The former can be measured from high-resolution maps of edge-on galaxies, the latter from spectral profiles of isolated regions in face-on disks.
Following van der Kruit and Shostak (1983) and references therein, let us assume that a spiral disk can be approximated by a self-gravitating sheet which is locally isothermal (i.e., the velocity dispersion of any of its components is independent of z). Then the total mass density can be expressed as
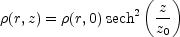 |
(12.7) |
where z0 may be a function of the distance from the center (in the plane), r. The HI disk can be assumed to be effectively massless, in comparison with other dynamically important components; it can then be shown that the HI density decreases to half of its midplane value at a height zH,
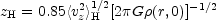 |
(12.8) |
where <vz2>H1/2 is the z-velocity dispersion of the gas and G is the gravitational constant. We can rewrite Equation (12.8) as
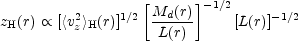 |
(12.9) |
where Md(r) is the disk mass within radius r and the luminosity profile L(r) is obtained from major-axis photometry. Measurements of <vH2>H1/2 have been made directly in a few face-on galaxies; all yield values in the range of 7 to 10 km s-1 and appear to vary relatively little with r. One can thus apply Equation (12.9) to a well-mapped edge-on object, such as NGC 891 or NGC 7814, for which zH(r) is then known. By assuming a value of <vz2>H1/2 as measured in face-on spirals, and by photometrically determining L(r), we can obtain the details of the (Md / L) ratio within the disk. Such an operation yields the following results:
The mass-to-luminosity ratio of the disk is independent of r, and hence the luminosity profile of the spiral disk is also a profile of the disk's mass.
Only one-third of the total mass of NGC 891 within the distance to the edge of the optical disk actually resides in the disk itself, the rest being distributed in a much thicker component, the halo.
At r = 10 kpc, the mass density of the disk at z = 0 exceeds that of the halo (assumed spherical) by a factor of 4; at r = 21 kpc, that ratio decreases to 2.
In the edge-on Sab galaxy NGC 7814, only a small fraction of the total mass, interior to the optical radius of 22 kpc, is in the disk; its light distribution, furthermore, is dominated by the spheroidal bulge. The rotation curve then can be used to sample the bulge's mass-to-light ratio; it is found to increase by a factor of 10 between the inner regions (r < 10) and 22 kpc.
In conclusion, the dynamical masses of spiral galaxies are found to be still growing linearly beyond the edges of their optical disks, at least out to the greatest radii at which gravitational potential tracers like HI are detectable. Within the optical radius, no more than one-third to one-half of the mass resides in the disk. The ratio between luminous and dynamical mass within the disk is about constant with radius and independent of morphological type, while that of the spheroidal component grows rapidly with distance from the galactic center.