12.4. THE VELOCITY WIDTH AS A DISTANCE INDICATOR

It is well know that there is a tight correlation between galaxy morphology and angular momentum, dominated in spirals by rotation. As a distance-independent quantity, the velocity width can be used in conjunction with some other observable to estimate the distance to a galaxy via a method that does not involve the redshift. Comparison of this "luminosity distance" with that predicted from the redshift serves as a means of deriving the Hubble constant and in identifying deviations from a smooth Hubble expansion. Calibration of the method relies on the assumption of known distances to a few nearby galaxies, obtained via primary indicators such as variable stars.

12.4.1. The Velocity Width-Magnitude Relation

As discussed in Section 12.3.1, the maximum rotational velocity reached within a galaxian disk depends on the luminosity of the galaxy, as described by Equation (12.5). In 1977, B. Tully and R. Fisher were the first to realize that such a circumstance lent itself to the measurement of distance moduli. They expressed the relationship in the form

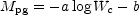(12.10)

where M_pg is the absolute photographic magnitude, corrected for both the extinction by dust in our galaxy and by dust in the target galaxy itself. The latter is generally parameterized by an inclination and a morphological-type dependence. W is the velocity width of the 21-cm line profile, integrated over the whole solid angle subtended by the HI in the galaxy after correction by a factor (csc i), where i is the inclination of the galaxian disk to the line of sight. The coefficients a and b were initially found to be about 6.25 and 3.5, respectively. Numerous authors successively applied the method, but doubts were cast on the legitimacy of the application of Equation (12.10). Brosche (1971) noted that the maximum velocity width observed is different for galaxies of different morphological type; later, Roberts (1978) pointed out that the velocity width-magnitude relation depends strongly on the morphological type, a result later confirmed by the detailed studies of systematic properties of rotation curves by Rubin and coworkers (1985). The slope of the relation, in fact, when considered for individual morphological types, is closer to 10; it was the combination of galaxies of several morphologies, each with a different offset b, which initially yielded a flatter relation. The offset between Sa's and Sc's is, according to Rubin et al., about 2 magnitudes, in the blue. Important contributions towards understanding the biases in the use of the velocity width-magnitude relation have been made by Bottinelli et al. (1986 and references therein), particularly in connection with the determination of the Hubble constant.

The sources of uncertainty in establishing values of a and b can be serious. The circumstance that optimizes the determination of W_c, i.e., high inclination, conspires to render more uncertain both the correction for internal extinction to M_pg and the determination of the morphological type, necessary to decide which values of a and b in Equation (12.10) should apply. Aaronson and coworkers first proposed in 1979 that most of the uncertainties associated with the inclination corrections are minimized if infrared rather than blue or photographic magnitudes are used. The interstellar extinction at 1.6 µm is practically negligible, and hence the uncertainty in the magnitude correction is practically eliminated. In addition, Aaronson and coworkers found no dependence in the coefficients of Equation (12.10) with morphological type, when the absolute magnitudes at 1.6 µm replace the photographic ones, and a reduced scatter about the best fit to the data. The quality of this correlation is illustrated in Figure 12.8, an infrared magnitude-velocity width plot for 306 nearby galaxies. Aaronson and coworkers have interpreted this apparently fortuitous and most convenient of circumstances as a natural consequence of using infrared magnitudes, given the properties of the stellar population they trace, but their interpretation has been disputed by Burstein (1982). Rubin et al. (1985) find that Equation (12.10) is not independent of morphological type even at infrared wavelengths. As with blue magnitudes, the slope of about a = 10 is virtually independent of type, but an offset of about 1.3 magnitudes separates Sa's from Sc's. They also find that the scatter in the relation is not significantly reduced (rms of 0.68 with blue magnitudes, 0.67 with infrared magnitudes) by adopting 1.6 - µ magnitudes. The differences between the results of Rubin et al. and those of Aaronson et al. probably reside in different biases inherent in the choice of samples.

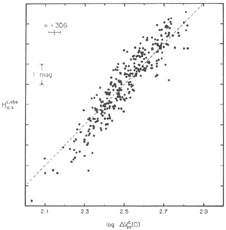Figure 12.8. Infrared magnitude-velocity width relation for 306 nearby galaxies, after Aaronson et al. (1982). Absolute magnitudes were calculated assuming a uniform Hubble flow. Dashed line has a slope of 10. Error bar represents the typical uncertainty for a single point, as estimated by the authors.

The physical basis for the velocity width-magnitude relation is poorly understood. (A possible interpretation was given in Section 12.3.1.) A similar relationship between the luminosity and velocity dispersion is seen among ellipticals, L ⁴, with a third parameter, the integrated surface brightness, providing the needed scale length to minimize the scatter. Indeed, equilibrium disk models with constant surface brightness and constant mass-to-light ratio predict L V⁴, but the application to all real galaxies is not clear.