Copyright © 2002 by Annual Reviews. All rights reserved
|
| Annu. Rev. Astron. Astrophys. 2002. 40:
643-680 Copyright © 2002 by Annual Reviews. All rights reserved |
With recent developments in instrumentation and observing strategies, it will soon be possible to image large areas with high sensitivity, enabling efficient and systematic SZE searches for galaxy clusters.
The primary motivation for large surveys for galaxy clusters using the SZE is to obtain a cluster catalog with a well understood selection function that is a very mild function of cosmology and redshift. There are two primary uses for such a catalog. The first is to use clusters as tracers of structure formation, allowing a detailed study of the growth of structure from z ~ 2 or 3 to the present day. The second use is for providing a well-understood sample for studies of individual galaxy clusters, either as probes of cosmology or for studies of the physics of galaxy clusters.
Numerous authors have presented estimates of the expected yields from SZE surveys (Korolev et al, 1986, Bond & Myers, 1991, Bartlett & Silk, 1994, Markevitch et al, 1994, De Luca et al, 1995, Bond & Myers, 1996, Barbosa et al, 1996, Colafrancesco et al, 1997, Aghanim et al, 1997, Kitayama et al, 1998, Holder et al, 2000b, Bartlett, 2000, Kneissl et al, 2001). Results from the diverse approaches to calculating the cluster yields are in broad agreement.
The number of clusters expected to be found in SZE surveys depends sensitively on the assumed cosmology and detector specifications. Estimates of the order of magnitude, however, should be robust and able to give a good indication of the expected scientific yields of surveys for galaxy clusters using the SZE.
In calculating the number of clusters expected in a given survey,
three things are needed:
1) the volume per unit solid angle
as a function of redshift,
2) the number density of clusters
as a function of mass and redshift, and
3) an understanding of the
expected mass range which should be observable with the particular SZE
instrument and survey strategy.
The physical volume per unit redshift per unit solid angle is given by (Peebles, 1994)
 |
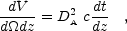(7) |
where dt / dz = 1 / [H(z)(1 + z)] and H(z) is the expansion rate of the universe. The comoving volume is simply the physical volume multiplied by (1 + z)3.
The number density of clusters as a function of mass and redshift can either be derived by applying the statistics of peaks in a Gaussian random field (Press & Schechter, 1974, Bond et al, 1991, Sheth et al, 2001) to the initial density perturbations or taken from large cosmological N-body simulations (Jenkins et al, 2001). The mass function is still not understood perfectly, with small but important differences between competing estimates, especially at the high mass end of the spectrum. Precise cosmological studies will require an improved understanding, but reasonably accurate results can be obtained with the "standard" Press-Schechter (Press & Schechter, 1974) mass function, with the comoving number density between masses M and M + dM given by
 |
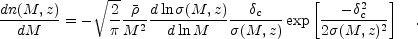(8) |
In the above,
is the
mean background density of the universe today,
2(M,
z) is the variance of the density field
when smoothed on a mass scale M, and
c (typically
~ 1.69) is the critical overdensity for collapse in the spherical
collapse model
(Peebles, 1980).
Smoothing the density field on a mass scale corresponds to finding the
comoving volume that encloses a given mass for a region at the mean
density of the universe and smoothing the density field over this
volume. The variance
2(M,
z) is separable as
(M, z)
(M)
D(z), where
(M) is the variance
in the initial density field and D(z) is the linear growth
function that indicates how the amplitude of the density field has grown
with time. For a universe with
M = 1
this growth function is simply proportional to the scale factor.
For a universe composed only of matter and vacuum energy (either with or without spatial curvature), accurate fitting functions for the growth function can be found in Carroll et al (1992) or can be found as a straightforward one-dimensional numerical integral, using the solution found by Heath (1977). For a more exotic universe, for example one with dark energy not in the form of a cosmological constant, the growth function requires solution of a two dimensional ordinary differential equation.
The Press-Schechter formulation has the advantage of making it clear
that the abundance of very massive objects is exponentially
suppressed, showing that massive clusters are expected to be rare. The
amount of suppression as a function of redshift is sensitive to the
linear growth function D(z), which is itself sensitive to
cosmological parameters. Structure grows most efficiently when the
universe has
M ~ 1, so
the growth function as a function
of z should give a good indication of the epoch when either
curvature, vacuum energy or dark energy started to become
dynamically important.
The exponential dependence of the cluster abundance makes SZE surveys a potentially powerful probe of cosmology. This is shown in Figure 7, where the relative importance of volume and number density can be seen. A difference in cosmology can cause a difference in volume of a few tens of percent, while the corresponding change in comoving number density is typically a factor of a few. This plot also shows the rapid decline in the number density of the cluster abundance with redshift and its steep dependence on mass, both of which are due to the exponential suppression of high peaks.
 |
Figure 7. Comoving volume element (left)
and comoving number density (center) for two cosmologies,
( |
The cosmology with the higher mass density can be seen to have a
higher abundance at z = 0 in Figure 7 for
a fixed normalization of the power spectrum, i.e.,
8. This is
primarily because a given cluster mass will correspond to a slightly
smaller size for a universe with higher matter density. The matter
power spectrum rises toward smaller scales, so a fixed amplitude of
the power spectrum on a specific scale will lead to a higher density
cosmology having more power on a given mass scale. Choosing a slightly
lower value of
8 for the
cosmology with the higher density
removes this offset in the cluster abundance at z = 0 and leads to a
lower cluster abundance at higher redshifts, i.e., if the cluster
abundance is normalized at z = 0 for all cosmological models, the
higher density models will have relatively fewer clusters at high
redshift. This can be seen in the right panel of
Figure 7, where the redshift distribution per square
degree has been normalized to give the same number of clusters above a
mass of 1014 h-1
M
at
z = 0 by lowering the normalization of the power spectrum from
8 = 0.90 to
0.75 for the cosmology with the higher matter density.
4.2. Mass Limits of Observability
The range of masses to which a survey is sensitive is set by the effective beam size and sensitivity of the instrument as well as the cluster profile on the sky. In the case of a beam that is larger than the cluster, a survey is limited by SZE flux. From equation 5, a flux limit corresponds to constant Ne T / DA2. The dependence on angular diameter distance rather than luminosity distance leads to a relative factor of (1 + z)4 when compared to a usual flux limit for emission from a distant source. Past z ~ 1 the angular diameter distance is slowly varying, and the gas temperature for a fixed mass should be higher than at z = 0, since the clusters are more dense and therefore more tightly bound, i.e., smaller. As a result, at z > 1 the limiting mass for an SZE survey is likely to be gently declining with redshift (Holder et al, 2000b, Bartlett, 2000, Kneissl et al, 2001). Nearby clusters (z < 0.2) are likely to be at least partially resolved by most SZE surveys, making the mass selection function slightly more difficult to estimate robustly. It is not expected that the mass threshold of detectability should change more than a factor of ~ 2 - 3 for clusters with z > 0.05, making an SZE selected catalog remarkably uniform in redshift in terms of its mass selection function.
The expected cluster profiles are not well known, since there are very few known clusters at z > 0.5, and these are much more massive than the typical clusters expected to be found in deep SZE surveys. The total SZE flux from a cluster should be fairly robust against changes in cluster profiles due to substructure or merging. Broadly speaking, the SZE is providing an inventory of hot electrons. The characteristic temperature in a cluster is set by virial considerations, since the electrons are mainly heated by shocks due to infall. Kinetic energy of infalling gas should be converted into thermal energy in a time shorter than the Hubble time, suggesting that the thermal energy per particle must necessarily be on the order of GM / R. Therefore, it is very difficult to substantially alter the expected SZE flux for a cluster of a given mass.
The mass limit of detection corresponding to an SZE flux limited survey is shown in the left panel of Figure 8. The two types of surveys shown correspond to deep ground-based imaging of a few tens of square degrees down to µK sensitivities with arcminute resolution or wide-field surveys (similar to the Planck Surveyor satellite) with ~ 5' - 10' resolution.
 |
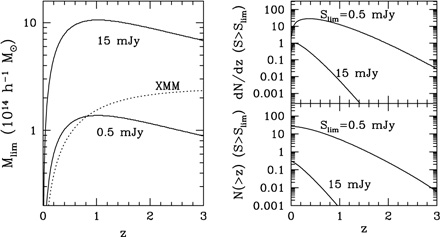Figure 8. Left: Mass limits as a function
of redshift for a typical
wide-field type of survey (equivalent to ~ 15 mJy at 30 GHz) and
a typical deep survey (~ 0.5 mJy). The approximate XMM
serendipitous survey limit is also shown. Right: Differential (top)
and cumulative (bottom) counts as a function of redshift for two SZE
surveys shown at left, assuming a
|
In contrast to the total integrated SZE flux, the concentration of SZE flux is very model dependent, with very compact clusters having high central decrements (or increments) but subtending a relatively small solid angle. The integrated SZE flux is thus a potentially very powerful criterion for controlling selection effects in samples for cluster studies. The clusters can first be found using integrated SZE flux and then investigated with high resolution SZE imaging.
4.3. Estimates of SZE Source Counts
The expected source counts are shown in the right panels of Figure 8. From the considerations discussed above, it should be clear that the exact numbers will depend on cosmology and observing strategy. A robust conclusion is that upcoming deep surveys should find tens of clusters per square degree. Less deep surveys, such as the all-sky Planck Surveyor satellite survey should detect a cluster in every few square degrees. The resulting catalogs should be nearly uniformly selected in mass, with the deep catalogs extending past z ~ 2.
=
(0.3, 0.7) (solid) and (0.5, 0.5) (dashed). For the middle panel, the
normalization of the matter power spectrum was taken to be