4. ENERGETIC PARTICLE ACCELERATION IN COLLISIONLESS SHOCKS

The reflected ions with a gyro-radius exceeding the width of the shock transition region can then be efficiently accelerated, via the Fermi mechanism, by converging plasma flows carrying magnetic inhomogeneities and MHD waves. In perpendicular shock a net transverse particle momentum gain is due to the work of the electric field on the particle drift motion. The electric field perpendicular to the shock normal exists in all the reference frames for the perpendicular shock. The particle of a momentum p crossing back and forth the shock front and being scattered by MHD waves carried with a flow of velocity u would undergo a momentum increment p p ⋅ u / v + O((u / v)²) per scattering. A velocity profile in the plane shock is illustrated by the dashed line in Fig. 5 in the test particle case where one neglects the back reaction effect of accelerated particles on the shock. One way to calculate the accelerated particle spectra in a scattering medium is to use the kinetic equation in the diffusion approximation. The scattering medium in that approach is characterised by momentum dependent particle diffusion coefficients k₁(p) and k₂(p). The shock is considered as a bulk velocity jump (see the dashed line in Fig. 5) assuming that the test particles are injected at p = p₀ and the gyroradii of the particles are larger than the shock width. Therefore, in a test particle case particles must be injected at some super-thermal energy to be accelerated by the shock. A solution to the kinetic equation for a nearly isotropic test particle distribution in the phase space is a power-law momentum distribution f(p, x) (p / p₀) ^{- b}, p p₀ where the index

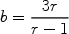(14)

depends on the shock compression ratio r (Axford et al. 1977, Krymskii 1977, Bell 1978, Blandford & Ostriker 1978). The CR spatial distribution in the model is illustrated in Fig. 5. For a strong shock of _s >> 1 and _a >> 1 the compression ratio given by Eqs. 6 and 8 is close to 4 if _g = 5/3 (or even larger if relativistic gas dominates the equation of state). The pressure of the accelerated particles is

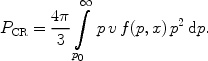(15)

Then for b = 4 one may see that P_CR ln(p_max / p₀) indicating a potentially large cosmic ray (CR) pressure, if CRs are accelerated to p_max >> p₀. The maximal energy of accelerated test particles depends on the diffusion coefficients, bulk velocity and scale-size of the system. The finite scale-size of the shock is usually accounted for by an energy dependent free escape boundary located either in the upstream or in the downstream. For electrons p_max can also be limited by synchrotron (or inverse-Compton) losses of relativistic particles.

Figure 5. A sketch illustrating the structure of a cosmic-ray modified shock. The dashed line is the shock velocity jump corresponding to the test particle case. The dotted line is a spatial distribution of accelerated particles at some momentum p >> p0. The solid line is the CR modified shock velocity profile with the precursor and subshock indicated.

The test particle shock acceleration time τ_a(p) can be estimated from the equation

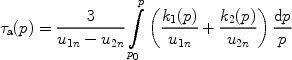(16)

where the normal components of the shock upstream and downstream bulk velocities u_1n, u_2n are measured in the shock rest frame. Estimations based on a more rigorous approach distinguishing between the mean acceleration time and the variance does not change the results substantially, given the uncertainties in the diffusion model.