5. COSMIC-RAY MODIFIED MULTIFLUID SHOCKS

The efficiency of the upstream plasma flow energy conversion into nonthermal particles could be high enough providing a hard spectrum of nonthermal particles up to some maximal energy . If the efficiency of ram energy transfer to the energetic particles is high enough, an extended shock precursor appears due to the incoming plasma flow deceleration by the fast particle pressure. The precursor scale L is of the order of (c / v_sh) - orders of magnitude larger than the width of the shock transition region (see Fig. 5). Here is the maximal mean free path of a particle in the energy-containing part of the spectrum and v_sh is the shock velocity. We shall later refer to these energetic particles as cosmic rays.

It has been shown that the front of a strong collisionless shock wave consists of an extended precursor and a viscous velocity discontinuity (subshock) of a local Mach number that is smaller than the total Mach number of the shock wave (see Fig. 5). The compression of matter at the subshock can be much lower than the total compression of the medium in the shock wave with allowance for high compression in the precursor. We shall refer later to such shocks as CR-modified.

The large scale ("macroscopic") structure of a CR-modified shock can be modelled by a two-fluid approach with a kinetic description of nonthermal particles (see e.g. Blandford & Eichler 1987, Berezhko et al. 1996, Malkov & Drury 2001, Blasi 2004 and references therein) or by a Monte Carlo method (e.g. Jones & Ellison 1991, Ellison et al. 1996). In both methods some suitable parameterisation of particle scattering process must be postulated a priori. Monte-Carlo simulations, however, have no assumption of isotropy for particle distributions, and that allows an internally self-consistent treatment of thermal particle injection. While the injection depends on the assumptions made for the particle pitch-angle scattering, these assumptions are applied equally to particles of all energies. The Monte Carlo technique eliminates a free injection parameter, which is present in all models based on the diffusion approximation and is used to set the injection efficiency. The strong feedback between injection, shock structure, and magnetic field amplification makes this property of the Monte Carlo technique particularly important. The Monte Carlo technique allows to iteratively obtain a shock velocity profile and particle distribution function conserving mass, momentum and energy fluxes taking into account the nonlinear feedback from the accelerated energetic particles.

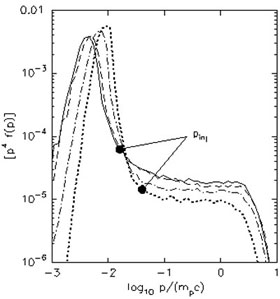
In Fig. 6 Monte Carlo simulated proton spectra (multiplied by [p / (m_pc)]⁴) are shown, in the downstream shock from Vladimirov et al. (2006). To illustrate the dependence of the maximal energy of an accelerated proton on the system scale size, a free escape boundary condition was applied at some distance from the subshock position in the shock rest frame. The heavy solid and dotted curves in the right panel correspond to the free escape boundary located at a distance 10⁴r_g1 (where r_g1 = m_p v_sh c / e B₁), the dashed curve has 10³r_g1, and the light solid curve has 10⁵r_g1. The simulations were done for a supernova shock in the interstellar medium with a shock speed v_sh = 5000 km s^-1 and an unshocked proton number density n₁ = 1 cm^-3. In the left panel the spectra are given for the same position of the free escape boundary, but for different prescriptions of the scattering model.

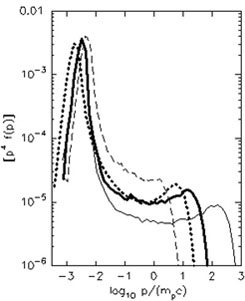Figure 6. Spectra of protons accelerated by a strong shock. The spectra were simulated with a non-linear Monte-Carlo model which accounts for particle injection and magnetic field amplification by the shock (for details see Vladimirov et al. 2006). On the left panel the transitions from the thermal-like component to the high energy tail are marked by pinj. On the right panel different curves correspond to different locations of the free escape boundary (see in the text).

5.1. Magnetic field amplification in CR-dominated shocks

An important predicted feature of strong shocks with efficient CR acceleration is the possibility to amplify an initial seed magnetic field by orders of magnitude (e.g. Bell & Lucek 2001, Bell 2004). CR current and CR pressure gradient upstream of the strong shock could drive magnetic fluctuations on the shock precursor scale length. The CR-shock precursor scale L is ~ (c / v_sh) which is expected to be above a kpc, moreover, the width is L 100 kpc for a shock of a size comparable to that of a galaxy cluster. The precursor scale size L is >> 10⁹ times larger than the subshock transition region where strong small scale magnetic field fluctuations are directly produced by instabilities of super-Alfvénic bulk plasma flows illustrated in Fig. 2. That small scale fluctuations are responsible for bulk plasma motion dissipation process and adiabatic amplification of the transverse magnetic field in collisionless shocks. At the same time the collisionless dissipation process is thought to inject a minor fraction of incoming particles to be accelerated to high energies by Fermi mechanism. Recent models of diffusive shock acceleration allows a substantial fraction (say, 30%) of the MHD shock ram pressure to be converted to accelerated particles filling a vicinity of the shock of the scale L. The large scale current and density gradient of the accelerated CRs may convert a fraction of the CR energy to magnetic field due to multifluid instabilities of different kinds providing a way to amplify the initial magnetic field by a factor larger than the shock compression ratio.

Recent non-linear simulations of magnetic field amplification in diffusive shock acceleration by a Monte-Carlo model (Vladimirov et al. 2006) and a kinetic model (Amato & Blasi 2006) confirmed the possibility of a significant effect. The amplitude of the fluctuating magnetic field energy density W_B is of the order of the shock accelerated CR pressure which is in turn a substantial fraction of the shock ram pressure 0.5 ₁ v_sh². Here ₁ is the shock upstream ambient gas density.

For typical cluster parameters the discussed mechanism could provide a µG range magnetic field amplitude in a hundred kpc range scale of CR-modified shock precursor. The Faraday rotation measure RM provided by a strong CR-dominated shock in a cluster can reach values of 10 rad m^-2 and even a few times higher. For the case of the so-called Bohm diffusion model the rotation measure RM is proportional to the maximal energy of the ions in the energy-containing part of the CR-spectrum accelerated by the shock. Radio observations, Faraday rotation and synchrotron-Compton emission measurements are used to estimate the magnetic fields in clusters (e.g. Carilli & Taylor 2002, Newman et al. 2002). Large filaments of polarised radio emission of scale size about 400 kpc were discovered by Govoni et al. (2005) in the halo of the cluster of galaxies Abell 2255 and by Bagchi et al. (2006) in Abell 3376 (see Fig. 8). They could be connected to large scale shocks due to accretion/merging activity of the cluster.

5.2. Gas heating and entropy production in strong CR-modified shocks

An exact modelling of a collisionless shock structure taking into account the nonthermal particle acceleration effect requires the nonperturbative self-consistent description of a multi-component and multi-scale system including strong MHD-turbulence dynamics. Such a modelling is not feasible at the moment. Instead, a simplified description of a multi-fluid strong shock structure can be used with an appropriate parameterisation of the extended pre-shock and of the gas subshock. The predicted observable characteristics of the shocks can be confronted to the observational data. We will now discuss the effects of plasma heating by modified shocks and then make some specific predictions for possible observational tests.

In the shocks with efficient high energy particle acceleration the energy flux carried away by escaping energetic particles Q_esc must be accounted for in the energy continuity equations. The energy loss results in a lower effective adiabatic index, but it allows to increase the total compression of the gas in the shock downstream.

The total compression ratio r_tot of a strong MHD shock modified by an efficient nonthermal particle acceleration can be estimated as

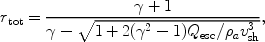(17)

assuming that the energy density in the shock upstream is dominated by the ram pressure and that the CR escape is through the cut-off momentum regime (e.g. Malkov & Drury 2001). Here is the effective adiabatic exponent. In Fig. 7 we illustrate the dependence of the compression ratio on Q_esc / _a v_sh³ for = 4/3 and 5/3 assuming that the effective adiabatic exponent is between the two values depending on the spectrum of the accelerated relativistic particles.

Figure 7. Total compression ratio rtot of a strong MHD shock modified by efficient particle acceleration as a function of the energy escape flux Qesc / kin carried by energetic particles, where kin = 1 vsh3/2. The upper curve (dotted) corresponds to an effective adiabatic exponent = 4/3 (relativistic gas), while the lower (solid) curve corresponds to = 5/3.

The distribution function of nonthermal particles and the bulk flow profile in the shock upstream region are sensitive to the total compression ratio r_tot. Thus, the exact calculation of the escape flux Q_esc can be performed only in fully nonlinear kinetic simulations. Nevertheless, an approximate iterative approach (e.g. in the Monte Carlo model discussed above) can be used to make the steady-state distribution function consistent with the shock compression assuming some diffusion model. The subshock is the standard gas viscous shock of a Mach number _sub. For that simplified two-fluid model of a strong CR-modified shock the effective ion temperature in the downstream T_i⁽²⁾ can be estimated for a shock of a given velocity, if r_tot and r_sub are known:

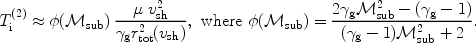(18)

Single fluid strong shock heating represents the limit _sub = _s >> 1, since there is no precursor in that case, resulting in Eq. 9. In single-fluid systems the compression ratio r_tot = r_sub (_g + 1) / (_g -1) does not depend on the shock velocity and Eq. 18 reduces to Eq. 9. However, in multi-fluid shocks the total compression ratio depends on the shock velocity and could be substantially higher than that in the single-fluid case. This implies somewhat lower postshock ion temperatures for the strong multi-fluid shock of the same velocity and could be tested observationally. It is convenient to introduce the scaling r_tot(v_sh) v_sh to describe the different cases of strong shock heating (see Bykov (2005) for details). Then from Eq. 18, T_i2 (_sub) v_sh^{2(1 - )}. The subshock Mach number _sub depends, in general, on _s and _a. Thus, an index approximates the velocity dependence of (_sub) v_sh. Finally, if T_i2 v_sh^a, then the index a = 2(1 - ) + . For the case of shock precursor heating by CR generated Alfvén waves, the index a 1.25 (Bykov 2005).

A distinctive feature of multi-fluid shocks is their high gas compression r_tot(v_sh) that could be well above the single fluid shock limit (_g + 1) / (_g - 1) (see Fig. 7). At the same time entropy production for a strong multi-fluid shock scales as r_tot(v_sh) ^{- (_g + 1)} and it is significantly reduced compared to the single-fluid shock of the same velocity. The effects are due to energetic particle acceleration and magnetic field amplification.

Energetic particles penetrate into the shock upstream region. They are coupled with the upstream gas through fluctuating magnetic fields (including the Alfvén waves generated by the energetic particles). Magnetic field dissipation provides gas preheating and entropy production in the extended shock precursor. Such a heated pre-shock region of kT 0.5 keV would appear as an extended filament of width L ~ (c / v_sh) 3 × 10¹⁴ B_-6^-1 cm. Here (in GeV) is the highest energy of the hard branch of the accelerated particle spectrum. If B_-6 ~ 0.1 in the cluster outskirts and if the hard spectrum of energetic nuclei extends to ~ 10⁹ GeV (cf. Norman et al. 1995) we have L ~ 1 Mpc and even wider. Projected on a hot X-ray cluster, such filaments could produce a soft X-ray component "excessive" to that produced by the hot cluster. A warm gas (~ 0.2 keV) emission filament found with XMM-Newton in the outskirts of the Coma cluster by Finoguenov et al. (2003) could be an extended heated precursor of a strong multi-fluid accretion shock. For a detailed review of the soft X-ray/EUV excesses see Durret et al. 2008 - Chapter 4, this volume.

5.3. ICM entropy production by multifluid accretion shocks

Cold gas falling into the dark matter (DM) dominated gravitational well passes through a strong accretion shock. The shock is a source of gas entropy production in the intercluster medium (ICM) (e.g. Knight & Ponman 1997, Tozzi & Norman 2001, Voit et al. 2003). The post-shock entropy K = K_b T / ^2/3 used in the ICM analysis and simulations (e.g. Bialek et al. 2001) is related to the standard thermodynamic entropy s through K exp(s / c_v). In the standard scenario with a single-fluid accretion shock the post-shock entropy scales K_sf v_sh² ₁^-2/3 (e.g. Voit et al. 2003).

The multi-fluid nature of the collisionless accretion shock modifies the standard scaling relation to be

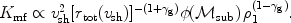(19)

The compression ratio in CR-shocks is higher than in a strong single-fluid shock of the same velocity resulting in reduced post-shock entropy production. For example, in the case of Alfvén heating the post-shock entropy of a multi-fluid shock reduces as K_mf / K_sf ~ (15 / _a) for _a > 15 and _s² > _a. Here and below in numerical estimations we assume _g = 5/3, though a non-thermal baryonic component could reduce the index _g.

Since r_tot(v_sh) and (_sub) are shock velocity dependent, the simple scaling K v_sh² ₁^-2/3 is not valid. In CR-modified shocks K_mf v_{sh 1}^{(1 - _g)} or K_mf T^/a, where = 2 - (1 + _g) + . For the case of Alfvén wave heating the index is 1.25 and K_mf is T^0.8 assuming _g = 5/3. Recently Ponman et al. (2003) and Piffaretti et al. (2005) found that the dispersion in the observed cluster entropy profiles is smaller if an empirical relation K T^0.65 is used instead of the standard K T (see also Pratt et al. 2006).

Consider the simple model of smooth accretion of cold gas through a strong accretion shock by Voit et al. (2003). The gas of velocity v_ac accretes at a rate _g through the shock at a radius r_ac where

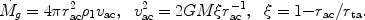(20)

Here M(t) is the cluster mass and r_ta is the matter turnaround radius. Then the entropy K_mf just behind the multi-fluid shock is expressed through T_i⁽²⁾(v_ac) and ₂ = r_tot(v_ac) ₁. In the Alfvén wave heating case K_mf(t) (Mt)^{(1 + ) / 3}, instead of K_sf(t) (Mt)^2/3 in the single-fluid regime. A multi-fluid shock results in a slower post-shock entropy production. As we have noted above, the regime of CR-shock compression depends on the plasma parameter in the infalling gas. The plasma parameter is currently poorly known because the intercluster magnetic fields are not well constrained. The effects of shock modifications are important for both the models of smooth accretion of cold gas and for accretion of hierarchical structures.

Preheating of accreting gas by different physical processes (e.g. due to early star formation in a protocluster region) was suggested by Evrard & Henry (1991), as a possible reason for the breaking of the scaling relations for pure gravitational cluster compression by [Kaiser 1986]. The observed high metallicity of clusters at different redshifts indicates that strong starburst activity was highly likely at some stage. The preheating produces some initial level of gas entropy ("entropy floor", see e.g. extensive simulations by Bialek et al. 2001, Borgani et al. 2001, Borgani et al. 2005). Multi-fluid strong shocks provide a natural alternative way of preheating accreting gas. The non-thermal components are essential for detailed modelling of global properties of X-ray clusters, including the mass-temperature and luminosity-temperature relations (Ostriker et al. 2005).