


At the basis of the analysis of the vertical dynamics of a stellar disk we have the Poisson equation for the case of axial symmetry and at low z (e.g. Oort 1965)
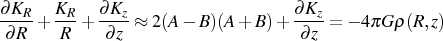 |
(4) |
For a flat rotation curve A = -B and 2(A - B)(A + B) = 0, so the plane-parallel case becomes an excellent approximation (van der Kruit & Freeman 1986). The equation of hydrostatic equilibrium
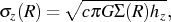 |
(5) |
relates the vertical velocity dispersion
 z(R)
of the old stars to the surface density
z(R)
of the old stars to the surface density
 so that if the mass-to-light ratio M / L is constant with
radius, the exponential radial surface brightness distribution
implies that
so that if the mass-to-light ratio M / L is constant with
radius, the exponential radial surface brightness distribution
implies that
 z(R)
should decline as the squareroot of
z(R)
should decline as the squareroot of
 or also as an
exponential with radius,
but with an e-folding of twice the scalelength h (the
constant c in eqn. (5) varies between 3/2 for an exponential with
n =
or also as an
exponential with radius,
but with an e-folding of twice the scalelength h (the
constant c in eqn. (5) varies between 3/2 for an exponential with
n =  in
eqn. (1) to 2 for an isothermal distribution with
n = 1). This was first tested in face-on spirals by van der Kruit
& Freeman
(1984,
1986),
where the prediction
was verified in detail in NGC 5347; in fact, the e-folding of
in
eqn. (1) to 2 for an isothermal distribution with
n = 1). This was first tested in face-on spirals by van der Kruit
& Freeman
(1984,
1986),
where the prediction
was verified in detail in NGC 5347; in fact, the e-folding of
 z was 2.4
± 0.6 photometric
scalelengths. Many studies have since confirmed this decrease of
z was 2.4
± 0.6 photometric
scalelengths. Many studies have since confirmed this decrease of
 z with radius
(e.g.
Bottema 1993,
Kregel et
al. 2004,
Kregel et
al. 2005)
and references therein).
z with radius
(e.g.
Bottema 1993,
Kregel et
al. 2004,
Kregel et
al. 2005)
and references therein).
There are two recent developments that have a very strong impact on this issue. The first is the use of integral field units that enable a more complete sampling of the disks. The so-called Disk Mass Project (Verheijen et al. 2007, Westfall et al. 2008) aims at a mapping of the stellar vertical velocity dispersion in this manner in about 40 face-on spiral galaxies. As above this will provide a kinematic measurement of the mass surface density of stellar disks. Not many results have appeared in the literature yet, but recent conference presentations show that the `kinematics follows the light', i.e. the velocity dispersions drop off according to the manner described above with constant M / L. The actual values indicate relatively low mass-to-light ratios that are well below those required for maximum disk fits (see below).
This result is also obtained in the other recent development, which is the use of planetary nebulae as test particles in disks (Herrmann & Ciardullo 2009) of five face-on spirals. This method allows the velocity dispersion of these representative stars of the old disk population to be measured out to large radii. In general the findings are the same: except for one system, the M / L is constant out to about three radial scalelengths of the exponential disks. Outside that radius the velocity dispersion stops declining and becomes flat with radius. Possible explanations these authors put forward for this behavior include an increase in the disk mass-to-light ratio, an increase in the importance of the thick disk, and heating of the thin disk by halo substructure. They also find that the disks of early type spirals have higher values of M / L and are closer to maximum disk than later-type spirals.
There is certainly support from stellar dynamics that in general there are no substantial gradients in mass-to-light ratios in disks. The rather low M / L values that are obtained currently do not require large amounts of material unaccounted for, as was found originally by Kapteyn (1922) and Oort (1932).
The stellar velocity dispersions in the plane are more complicated
to determine from observations. The radial and tangential ones are not
independent, but governed by the local Oort constants:

 /
/
 R =
(-B / (A - B))1/2.
This results from the axis ratio of the epicyclic motion that describes
stellar orbits deviating little from circular. The
frequency in the epicycle is
R =
(-B / (A - B))1/2.
This results from the axis ratio of the epicyclic motion that describes
stellar orbits deviating little from circular. The
frequency in the epicycle is
 =
2(-B(A - B))1/2 and its axis
ratio (-B / (A - B))1/2
(Oort 1965).
For a flat rotation curve A = -B, so
=
2(-B(A - B))1/2 and its axis
ratio (-B / (A - B))1/2
(Oort 1965).
For a flat rotation curve A = -B, so

 /
/  R
(the `axis ratio of tghe velocity ellipsoid') is 0.71 and
R
(the `axis ratio of tghe velocity ellipsoid') is 0.71 and
 = 21/2
Vrot / R.
= 21/2
Vrot / R.
In highly inclined or edge-on systems the dispersions can be meaured both from the line profiles and the asymmetric drift equation
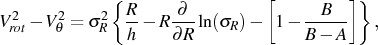 |
(6) |
where the circular velocity Vrot can be measured with
sufficient accuracy from the gas (optical emission lines or HI
observations), which have velocity dispersions of order 10 km/s or less
and therefore very little asymmetric drift (Vrot -
V ).
).
The radial dispersion plays an important role in the Toomre (1964) Q-criterion for local stability in galactic disks
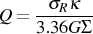 |
(7) |
with  the local mass
surface density. On
small scales local stability results from a Jeans-type stability, where the
tendency to collapse under gravity is balanced by the kinetic energy in
random motions, but only up to a certain (Jeans) scale. On large scales,
shear as a result of galactic
differential rotation provides stability. In the Toomre Q-criterion
the smallest scale for this is just equal to the Jeans scale, so that
that local stabiltiy exists on all scales. According to
Toomre (1964),
local stability requires Q > 1. Numerical simulations suggest
that galaxy disks have Q = 1.5-2.5 and are on the verge
of instability
(Hohl 1971,
Sellwood &
Carlberg 1984,
Athanassoula &
Sellwood 1986,
Mihos et al. 1997,
Bottema 2003).
the local mass
surface density. On
small scales local stability results from a Jeans-type stability, where the
tendency to collapse under gravity is balanced by the kinetic energy in
random motions, but only up to a certain (Jeans) scale. On large scales,
shear as a result of galactic
differential rotation provides stability. In the Toomre Q-criterion
the smallest scale for this is just equal to the Jeans scale, so that
that local stabiltiy exists on all scales. According to
Toomre (1964),
local stability requires Q > 1. Numerical simulations suggest
that galaxy disks have Q = 1.5-2.5 and are on the verge
of instability
(Hohl 1971,
Sellwood &
Carlberg 1984,
Athanassoula &
Sellwood 1986,
Mihos et al. 1997,
Bottema 2003).
The first study where an attempt was made to measure these velocity dispersions was by van der Kruit & Freeman (1986) on the highly inclined galaxy NGC 7184. They fitted their data using two different assumptions for the radial dependence of the radial velocity dispersion, one being that the axis ratio of the velocity ellisoid is the same everywhere, and the other that Toomre Q is constant with radius. Over the range from the center of one or two scalelengths the assumptions work out to similar variations (see van der Kruit 1990, page 196).
More extensive observations on a sample of 12 galaxies (including the Milky Way Galaxy from Lewis & Freeman 1989) by Bottema (1993) resulted in the discovery of a relation between a fiducial value of the velocity dispersion (either the vertical one measured at or extrapolated to the center or the radial velocity dispersion at one schalelength) and the integrated luminosity or the rotation velocity (equivalent through the Tully-Fisher relation). This has been confirmed (see fig. 1) by Kregel & van der Kruit (2005) and Kregel et al. (2005):
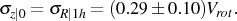 |
(8) |
It actually extends to small dwarf galaxies, e.g. 19 km sec-1 in UGC 4325 (Swaters 1999, chapter 7). Interestingly, the scatter in this relation is not random. Galaxies below the relation (with lower velocity dispersions) have higher flattening, lower central surface brightness or dynamical mass (4 h Vrot2 / G) to disk luminosity ratio.
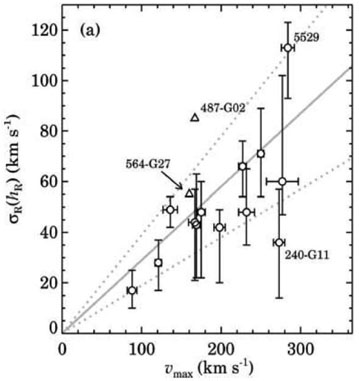 |
Figure 1. Stellar disk velocity dispersion,
measured at one scalelength in edge-on galaxies versus the
maximum rotational velocity. The gray lines indicate the relation
|
The linear  -
Vrot relation follows from straightforward arguments
(van der Kruit
1990,
Bottema 1993,
van der Kruit
& de Grijs 1999).
We evaluate now properties at one radial scalelength (R = 1
h). For a flat rotation curve and eliminating h
using a Tully-Fisher relation Ldisk
-
Vrot relation follows from straightforward arguments
(van der Kruit
1990,
Bottema 1993,
van der Kruit
& de Grijs 1999).
We evaluate now properties at one radial scalelength (R = 1
h). For a flat rotation curve and eliminating h
using a Tully-Fisher relation Ldisk
 µo h2
µo h2
 Vrot4 results in
Vrot4 results in
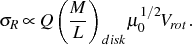 |
(9) |
This shows that when Q and M / L are constant among galaxies, the Bottema relation itself results and galaxy disks with lower (face-on) central surface brightness µo have lower stellar velocity dispersions than the mean.