Annu. Rev. Astron. Astrophys. 2010. 48: 673-710 Copyright © 2010 by Annual Reviews. All rights reserved

1. INTRODUCTION

In 1929 Carnegie astronomer, Edwin Hubble, published a linear correlation between the apparent distances to galaxies and their recessional velocities. This simple plot provided evidence that our Universe is in a state of expansion, a discovery that still stands as one the most profound of the twentieth century (Hubble 1929a). This result had been anticipated earlier by Lemaître (1927), who first provided a mathematical solution for an expanding universe, and noted that it provided a natural explanation for the observed receding velocities of galaxies. These results were published in the Annals of the Scientific Society of Brussels (in French), and were not widely known.

Using photographic data obtained at the 100-inch Hooker telescope situated at Mount Wilson CA, Hubble measured the distances to six galaxies in the Local Group using the Period-Luminosity relation (hereafter, the Leavitt Law) for Cepheid variables. He then extended the sample to an additional 18 galaxies reaching as far as the Virgo cluster, assuming a constant upper limit to the brightest blue stars (HII regions) in these galaxies. Combining these distances with published radial velocity measurements (corrected for solar motion) Hubble constructed Figure 1. The slope of the velocity versus distance relation yields the Hubble constant, which parameterizes the current expansion rate of the Universe.

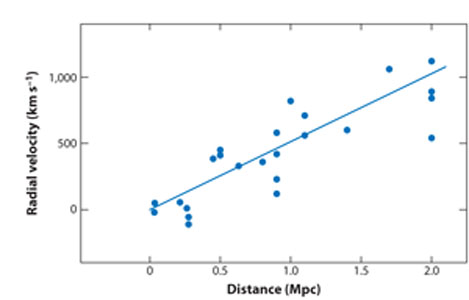Figure 1. From Hubble (1929a): radial velocities, corrected for solar motion, plotted versus distances estimated from stars and mean luminosities of galaxies in clusters. The solid dots and line represent the solution for solar motion using individual galaxies. Hubble wrote: "The outstanding feature, however, is the possibility that the velocity-distance relation may represent the de Sitter effect, and hence that numerical data may be introduced into discussions of the general curvature of space."

The Hubble constant is usually expressed in units of kilometers per second per megaparsec, and sets the cosmic distance scale for the present Universe. The inverse of the Hubble constant has dimensions of time. Locally, the Hubble law relates the distance to an object and its redshift: cz = H_od, where d is the distance to the object and z is its redshift. The Hubble law relating the distance and the redshift holds in any Friedman-Lemaitre-Robertson-Walker cosmology (see Section 2) for redshifts less than unity. At greater redshifts, the distance-redshift relationship for such a cosmology also depends on the energy densities of matter and dark energy. The exact relation between the expansion age and the Hubble constant depends on the nature of the mass-energy content of the Universe, as discussed further in Section 2 and Section 6. In a uniformly expanding universe, the Hubble parameter, H(t), changes as a function of time; H_o, referred to as the Hubble constant, is the value at the current time, t_o.

Measurement of the Hubble constant has been an active subject since Hubble's original measurements of the distances to galaxies: the deceptively simple correlation between galaxy distance and recession velocity discovered eighty years ago did not foreshadow how much of a challenge large systematic uncertainties would pose in obtaining an accurate value for the Hubble constant. Only recently have improvements in linear, solid-state detectors, the launch of the Hubble Space Telescope (HST), and the development of several different methods for measuring distances led to a convergence on its current value.

Determining an accurate value for H_o was one of the primary motivations for building HST. In the early 1980's, the first director of the Space Telescope Science Institute, Riccardo Giacconi, convened a series of panels to propose observational programs of significant impact requiring large amounts of Hubble observations. He was concerned that in the course of any regular time allocation process there would be reluctance to set aside sufficient time to complete such large projects in a timely manner. For decades a `factor-of-two' controversy persisted, with values of the Hubble constant falling between 50 and 100 km s^-1 Mpc^-1. A goal of 10% accuracy for H_o was designated as one of HST's three "Key Projects". (The other two were a study of the intergalactic medium using quasar absorption lines, and a "medium-deep" survey of galaxies.)

This review is organized as follows: We first give a brief overview of the cosmological context for measurements of the Hubble constant. We discuss in some detail methods for measuring distances to galaxies, specifically Cepheids, the tip of the red giant branch (TRGB), masers, the Tully-Fisher relation and Type Ia supernovae (SNe Ia). We then turn to a discussion of H_o, its systematic uncertainties, other methods for measuring H_o, and future measurements of the Hubble constant. Our goal is to describe the recent developments that have resulted in a convergence to better than 10% accuracy in measurements of the Hubble constant, and to outline how future data can improve this accuracy. For wide-ranging previous reviews of this subject, readers are referred to those of Hodge (1982), Huchra (1992), Jacoby et al. (1992), van den Bergh (1992), Jackson (2007), and Tammann, Sandage & Reindl (2008). An extensive monograph by Rowan-Robinson (1985) details the history of the subject as it stood twenty-five years ago.