Copyright © 2010 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 2010. 48:
673-710 Copyright © 2010 by Annual Reviews. All rights reserved |
Excellent introductions to the subject of cosmology can be found in Kolb & Turner (1990) and Dodelson (2003). We give a brief description here to provide the basis for the nomenclature used throughout this review. The expansion of a homogeneous and isotropic universe can be described by a Friedmann-Lemaitre-Robertson-Walker (FLRW) cosmology, which is characterized by parameters that describe the expansion, the global geometry, and the general composition of the universe. These parameters are all related via the Friedmann equation, derived from the Einstein general relativity field equations:
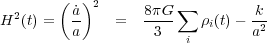 |
(1) |
where H(t) is the expansion rate, G is the Newtonian
gravitational
constant, a(t) is the cosmic scale factor characterizing the
relative size of the universe at time t to the present scale,
 i(t) are the individual components of
the matter-energy density, and k (with values of +1, 0, or -1)
describes the global geometry of the universe. The density
i(t) are the individual components of
the matter-energy density, and k (with values of +1, 0, or -1)
describes the global geometry of the universe. The density
 i
characterizes the matter-energy composition of the universe: the sum of
the densities of baryons, cold dark matter, and hot dark matter, and the
contribution from dark energy. Dividing by H2, we may rewrite
the Friedmann equation as
i
characterizes the matter-energy composition of the universe: the sum of
the densities of baryons, cold dark matter, and hot dark matter, and the
contribution from dark energy. Dividing by H2, we may rewrite
the Friedmann equation as
 total - 1 =
total - 1 =
 k = k /
(a2H2). For
the case of a spatially flat universe (k = 0),
k = k /
(a2H2). For
the case of a spatially flat universe (k = 0),
 total = 1.
total = 1.
In a matter-dominated universe, the expansion velocity of the Universe slows down over time owing to the attractive force of gravity. However, a decade ago two independent groups (Perlmutter et al. 1999; Riess et al. 1998) found that supernovae at z ~ 0.5 appear to be about 10% fainter than those observed locally, consistent instead with models in which the expansion velocity is increasing; i.e., a universe that is accelerating in its expansion. Combined with independent estimates of the matter density, these results are consistent with a universe in which one third of the overall density is in the form of matter (ordinary plus dark), and two thirds is in a form having a large, negative pressure, termed dark energy. In this current standard model the expansion rate of the Universe is given by
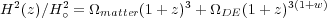 |
(2) |
where
 matter and
matter and
 DE refer
to the densities of (ordinary, cold and hot dark) matter and dark
energy, respectively, and w = p /
DE refer
to the densities of (ordinary, cold and hot dark) matter and dark
energy, respectively, and w = p /
 is the
equation of state of the dark energy, the
ratio of pressure to energy density. Recent observations by the
Wilkinson Microwave Anisotropy Probe (WMAP), based on entirely
independent physics, give results consistent with the supernova data
(Komatsu et al. 2009;
Dunkley et al. 2009).
Under the assumption of a
flat universe, the current observations of distant supernovae and
measurements by the WMAP satellite are consistent with a cosmological
model where
is the
equation of state of the dark energy, the
ratio of pressure to energy density. Recent observations by the
Wilkinson Microwave Anisotropy Probe (WMAP), based on entirely
independent physics, give results consistent with the supernova data
(Komatsu et al. 2009;
Dunkley et al. 2009).
Under the assumption of a
flat universe, the current observations of distant supernovae and
measurements by the WMAP satellite are consistent with a cosmological
model where
 matter = 0.3,
matter = 0.3,
 vacuum =
0.7, and w = -1. The observations are inconsistent with
cosmological models without dark energy.
vacuum =
0.7, and w = -1. The observations are inconsistent with
cosmological models without dark energy.
Another critical equation from general relativity involving the second derivative of the scale factor is:
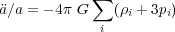 |
(3) |
where the sum is over the different contributions to the mass-energy density of the Universe. According to this equation, both energy and pressure govern the dynamics of the Universe, unlike the case of Newtonian gravity where there is no pressure term. It also allows the possibility of negative pressure, resulting in an effective repulsive gravity, consistent with the observations of the acceleration.
Any component of the mass-energy density can be parameterized by its
ratio of pressure to energy density,
w. For ordinary matter w =
0, for radiation w = 1/3, and for the cosmological constant
w =
-1. The effect on  / a of an individual component is
-4
/ a of an individual component is
-4 G
G
 i(1
+ 3wi). If w < -1/3 that
component will drive an acceleration (positive
i(1
+ 3wi). If w < -1/3 that
component will drive an acceleration (positive
 ) of the Universe. The
time evolution of the equation of state is unknown; a convenient, simple
parameterization is w(a) = wo + (1 -
a)wa, where wo characterizes
the current value of w and wa its derivative.
) of the Universe. The
time evolution of the equation of state is unknown; a convenient, simple
parameterization is w(a) = wo + (1 -
a)wa, where wo characterizes
the current value of w and wa its derivative.