Copyright © 2010 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 2010. 48:
673-710 Copyright © 2010 by Annual Reviews. All rights reserved |
The importance of pinning down Ho has only grown with time: not only does it set the scale for all cosmological distances and times, but its accurate determination is also needed to take full advantage of the increasingly precise measurements of other cosmological quantities. The prospects for improving the accuracy of Ho within the next decade appear to be as exciting as those within the past couple of decades. We highlight here near-term improvements to the Cepheid-based extragalactic distance scale that will come from new measurements of Cepheid parallaxes with GAIA and perhaps the Space Interferometry Mission (SIM), Spitzer measurements of Cepheids in the Milky Way, LMC, and other nearby galaxies, including NGC 4258, Spitzer measurements of the Tully-Fisher relation and a new calibration of the Type Ia supernova distance scale; and future measurements of Cepheids with JWST. We describe how a more accurate value of Ho, combined with other future measurements of large-scale structure and CMB anisotropies (e.g., Planck), can be used to break degeneracies and place stronger constraints on other cosmological parameters including the equation of state for dark energy, the energy density in cold dark matter, and the mass of neutrinos.
While measurements of CMB anisotropies have provided dramatic confirmation of the standard concordance model, it is important to keep in mind that the values for many quantities (e.g., w, Ho, neutrino masses) are highly model-dependent, owing to the strong degeneracies. A more accurate, independent measurement of Ho is critical for providing stronger limits on quantities such as w and neutrino masses.
7.1. Constraints on Dark Energy
As summarized by Hu (2005), a measurement of Ho to the percent level, in combination with CMB measurements with the statistical precision of the Planck satellite offers one of the most precise measurements of the equation of state at z ~ 0.5. At first this result appears counter-intuitive, since the CMB anisotropies result from physical processes imprinted on the surface of last scattering at z ~ 1100. Alone they give very little information on dark energy, which contributes most to the expansion at lower redshifts. However, the sound horizon provides a reference standard ruler that can be used to provide constraints on a number of parameters including dark energy and neutrinos. The main deviations in the Hubble parameter, the angular diameter distance, and the growth factor due to the dark energy equation of state manifest themselves as variations in the local Hubble constant. In Figure 12, we show the strong degeneracy between the equation of state and the value of Ho. This figure is based on a forecast of the precision that will be available with measurements of CMB fluctuations from the Planck satellite. Improved accuracy in the measurement of Ho will be critical for constraining the equation of state for dark energy from CMB data.
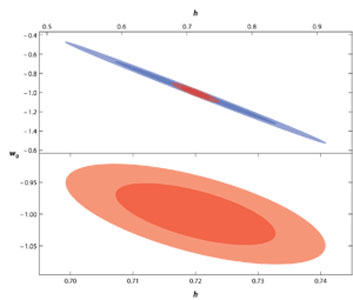 |
Figure 12. Upper Panel: A plot illustrating
the degeneracies of wo
with h = (Ho / 100) assuming the statistical
uncertainties expected for the Planck satellite, assuming a flat universe
( |
7.2. Constraints on the Neutrino Mass
Improved accuracy in the measurement of Ho will have a
significant
effect in placing constraints on the neutrino mass from measurements
of CMB anisotropies. Detailed reviews of the subject can be found in
Dolgov (1996),
Crotty, Lesgourges &
Pastor (2004)
and
Hannestad (2006).
Briefly, massive neutrinos contribute to the overall matter
density of the Universe through which they have an impact on the
growth of structure; the larger the neutrino mass, the more
free-streaming effects dampen the growth of structure on small
scales. The density in neutrinos is related to the number of massive
neutrinos, Neff, and the neutrino mass,
m , by:
, by:

 h2 = Neff
m
h2 = Neff
m / 94
eV. From neutrino oscillation experiments,
a measurement of the difference in mass squared,
/ 94
eV. From neutrino oscillation experiments,
a measurement of the difference in mass squared,
 m2 ~
0.002 (eV)2 is obtained.
m2 ~
0.002 (eV)2 is obtained.
In the context of the standard cosmological model, cosmological
observations can constrain the number of neutrino species and the
absolute mass scale. Massive neutrinos have a measurable effect on the
cosmic microwave background spectrum: the relative height of the
acoustic peaks decrease with increasing
m and the
positions of
the peaks shift to higher multipole values. The WMAP 5-year data
provided evidence, for the first time, for a non-zero neutrino
background from CMB data alone, with
and the
positions of
the peaks shift to higher multipole values. The WMAP 5-year data
provided evidence, for the first time, for a non-zero neutrino
background from CMB data alone, with
 m
m < 1.3 eV (95% CL)
(Dunkley et al. 2009).
Combining the CMB data with results from SNe Ia
and baryon acoustic oscillations, results in a bound of
< 1.3 eV (95% CL)
(Dunkley et al. 2009).
Combining the CMB data with results from SNe Ia
and baryon acoustic oscillations, results in a bound of
 m
m < 0.58 eV (95% CL)
(Komatsu et al. 2010),
reaching close to the range
implied by the neutrino oscillation experiments. Future forecasts with
Planck data suggest that an order of magnitude increase in accuracy
may be feasible. One of the biggest limitations to determining the
neutrino mass from the CMB power spectrum results from a strong
degeneracy between the neutrino mass and the Hubble constant
(Komatsu et al. 2009).
As Ho increases, the neutrino mass becomes
smaller (see Figure 13). An accuracy in
Ho to 2-3% percent,
combined with Planck data (for the standard cosmological model) will
provide an order of magnitude improved precision on the neutrino mass.
< 0.58 eV (95% CL)
(Komatsu et al. 2010),
reaching close to the range
implied by the neutrino oscillation experiments. Future forecasts with
Planck data suggest that an order of magnitude increase in accuracy
may be feasible. One of the biggest limitations to determining the
neutrino mass from the CMB power spectrum results from a strong
degeneracy between the neutrino mass and the Hubble constant
(Komatsu et al. 2009).
As Ho increases, the neutrino mass becomes
smaller (see Figure 13). An accuracy in
Ho to 2-3% percent,
combined with Planck data (for the standard cosmological model) will
provide an order of magnitude improved precision on the neutrino mass.
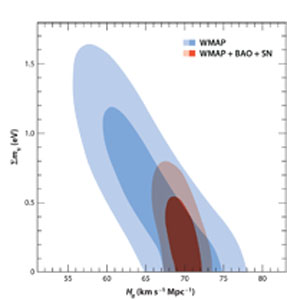 |
Figure 13. WMAP5 data showing the degeneracy between the sum of neutrino masses and Ho (Figure 17, Komatsu et al. 2009). The blue contours show the WMAP5 data only (68% and 95% CL; the red contours include BAO and SNe Ia data. |
Accuracy in measurement of Ho has improved signficantly with the measurement of HST Galactic Cepheid parallaxes and HST measurement of Cepheid distances to SNe Ia hosts, as described in Section 3.1.4 and Section 3.6.2, respectively. Future improvements will come with further HST WFC3 and Spitzer observations of Cepheids. At 3.6 and 4.5µm the effects of extinction are a factor of ~ 20 smaller in comparison to optical wavelengths. In addition, in the mid-infrared, the surface brightness of Cepheids is insensitive to temperature. The amplitudes of the Cepheids are therefore smaller and due to radius variations alone. The Leavitt Law in the mid-IR then becomes almost equal to the Period-Radius relation. From archival Spitzer data, the mid-infrared Leavitt Law has been shown to have very small dispersion (Freedman et al. 2008; Madore et al. 2009). Furthermore, metallicity effects are expected to be small in the mid infrared, and Spitzer offers an opportunity to test this expectation empirically. The calibration can be carried out using Spitzer alone, once again eliminating cross-calibration uncertainties. A new program aimed at addressing remaining systematic errors in the Cepheid distance scale is the Carnegie Hubble Program (CHP: Freedman 2009).
The CHP will measure the distances to 39 Galactic Cepheids (15 of them in anticipation of the GAIA satellite), 92 well-observed Cepheids in the LMC, several Local Group galaxies containing known Cepheids (M31, M33, IC 1613, NGC 6822, NGC 3109, Sextans A, Sextans B and WLM), more distant galaxies with known Cepheids including NGC 2403 (2.5 Mpc), Sculptor Group galaxies NGC 300, NGC 247 (3.7 Mpc), Cen A (3.5 Mpc) and M83 (4.5 Mpc), as well as the maser galaxy NGC 4258 (at 7.2 Mpc). It will measure the distances to 545 galaxies in 35 clusters with measured Tully-Fisher distances, which can then be calibrated with Cepheids as shown in Figure 7. Over 50 galaxies with SNe Ia distances measured by Folatelli et al. (2010) will also be observed as part of this program, allowing a determination of Ho with this calibration well into the far-field Hubble flow.
As discussed earlier, the expected uncertainties from the CHP are shown in Table 2. Re-observing the known Cepheids in more distant galaxies will require the aperture, sensitivity and resolution of JWST. With Spitzer, it will be possible to decrease the uncertainties in the Cepheid distance scale to the (3-4%) level, with an application of a new mid-IR Tully-Fisher relation and a Spitzer Cepheid calibration of Type Ia SNe. It is expected that future JWST measurements will bring the uncertainties to ± 2% with a more firm calibration of SNe Ia.