


Over the years a number of mathematical functions have been used to represent the radial distribution of stellar light in elliptical galaxies, i.e. their light profiles. Before getting to de Vaucouleurs' R1/4 model in the following paragraph, it seems apt to first quickly mention some early competitors. Although Plummer's (1911) internal-density model was developed for the nebulae which became know as globular clusters, because of its simplicity it is still used today by some researchers to simulate elliptical galaxies, even though, it should be noted, no modern observers use this model to describe the radial distribution of light in elliptical galaxies. Reynold's (1913) surface-density model, sometimes referred to as Hubble's (1930) model or the Reynold-Hubble model, was used to describe the nebula which became known as elliptical galaxies. It has an infinite mass and is also no longer used by observers today. The modified Hubble model (Rood et al. 1972), which also has an infinite mass, is also still sometimes used by simulators, even though, again, observers do not use this model anymore. Oemler's (1976) exponentially-truncated Hubble model, known as the Oemler-Hubble model, is also not used to represent the observed stellar distribution in elliptical galaxies because it too, like its predecessors, was simply an approximation applicable over a limited radial range, as noted by King (1978). It is interesting to note that up until the 1980s, departures at large radii from the Reynold's model were attributed to tidal-stripping by external gravitational potentials. That is, for three quarters of a century, Reynold's model - originally developed from low-quality data for one galaxy - was generally thought to describe the original, undisturbed stellar distribution in elliptical galaxies.
de Vaucouleurs' (1948, 1953) R1/4 surface-density model had traction for many years, in part due to de Vaucouleurs (1959) arguing that it fits better than the Reynold's model used by Hubble, - a point re-iterated by Kormendy (1977a) and others - and the revelation that it fits the radially-extended data for NGC 3379 exceedingly well (de Vaucouleurs & Capaccioli 1979). Hodge (1961a, b) had however revealed that de Vaucouleurs' model was inadequate to describe faint elliptical galaxies and Hodge (1963, 1964), in addition to King (1962) 6, noted that the 3-parameter King model, with its flatter inner profile and steeper decline at large radii, did a better job. For a time, King's (1962, 1966) model became popular for describing the light distribution in faint elliptical galaxies, at least until the exponential model - also used for the discs of spiral galaxies - was noted to provide a good description of some dwarf elliptical galaxies (Hodge 1971; Faber & Lin 1983; Binggeli et al. 1984) and that these galaxies need not have experienced any tidal truncation (a prescription of the King model with its tidal radius parameter). Lauer (1984, 1985) additionally showed that King's modified isothermal model, with its flat inner core, was inadequate to describe the deconvolved light-profiles of ordinary elliptical galaxies with "cores", i.e. galaxies whose inner light profile displays a nearly flat core. King's model does however remain extremely useful for studies of star clusters, globular clusters 7, dwarf spheroidal galaxies and galactic satellites which, unlike ordinary elliptical galaxies, can have flat cores in their inner surface brightness profile.
Today, the model of choice for describing nearby (and distant) dwarf and ordinary elliptical galaxies is Sérsic's (1963) generalisation of de Vaucouleurs' R1/4 model to give the R1/n surface-density model (section 2.1). This model reproduces the exponential model when n = 1 and de Vaucouleurs' model when n = 4; it can thus describe the main body of faint and luminous elliptical galaxies. The key advantage that this model has is (i) its ability to describe the observed stellar distributions that have a range of central concentrations (known to exist since at least Reaves 1956) and (ii) it provides a very good description of the data over (almost) the entire radial extent. Indeed, departures in the light profile from a well-fit Sérsic's model invariably signal the presence of additional features or components, rather than any failing of the model. Expanding upon the Sérsic model, the core-Sérsic model (section 2.2) is nowadays used to quantify those galaxies with "cores".
Although referring to the King model, the following quote from King (1966) seems particularly insightful "... de Vaucouleurs' law appears to refer to a particular central concentration and should be appropriate only for galaxy profiles that have that concentration." While noted by others, such as Oemler (1976), Capaccioli (1985), Michard (1985) and Schombert (1986), some three decades elapsed before the relevance of King's remark to elliptical galaxies re-surfaced - albeit slowly at first - in the 1990s. Indeed, de Vaucouleurs' useful, albeit limited, R1/4 model was referred to as a "law" for nearly half a century. However we are now more keenly aware that (even normal) elliptical galaxies possess a range of central concentrations: concentrations which are well quantified in terms of the exponent n in Sérsic's R1/n model (see Trujillo, Graham & Caon 2001; Graham, Trujillo & Caon 2001). Although, it should be confessed that one can still encounter papers which use R1/4 model parameters alongside some model-independent measure of galaxy concentration, unaware of the inconsistency arising from the fact that every R1/4 model actually has exactly the same level of concentration.
Before introducing the equation for Sérsic's model in the following section, it is pointed out that in addition to modelling what can be considered the main body of the galaxy, one can also find excess stellar light at (i) small radii in the form of nuclear (i.e. centrally located) discs and dense nuclear star clusters (section 2.3) and also at (ii) large radii in the form of halos or envelopes in cD and central cluster galaxies (section 2.4). As briefly noted above, deficits of stellar flux at the cores of massive galaxies are also observed, and a model to quantify these stellar distribution, relative to the outer non-depleted light profile, is described in section 2.2. While non-symmetrical components in elliptical galaxies can also exist, they are not addressed here given the focus on well-structured systems. Somewhat random, non-symmetrical components may be a sign of a disturbed morphology (see E.Barton's Chapter in this volume), of on-going non-uniform star formation (see S.Boissier's Chapter in this volume) or gravitationally-induced tidal features from external forces.
José Sérsic's (1963, 1968) R1 / n model, which was introduced in Spanish, describes how the projected surface-intensity I varies with the projected radius R, such that
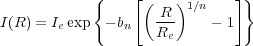 |
(1) |
and Ie is the intensity at the `effective' radius
Re
that encloses half of the total light from the model
(Ciotti 1991;
Caon et al. 1993).
The term bn
( 1.9992n-0.3271 for 0.5 < n < 10,
Capaccioli 1989)
is not a parameter but is instead
dependent on the third model parameter, n, that describes the
shape, i.e. the concentration, of the light profile.
8
The exact value of bn is obtained by solving the equation
1.9992n-0.3271 for 0.5 < n < 10,
Capaccioli 1989)
is not a parameter but is instead
dependent on the third model parameter, n, that describes the
shape, i.e. the concentration, of the light profile.
8
The exact value of bn is obtained by solving the equation
 (2n) =
2
(2n) =
2 (2n, bn) where
(2n, bn) where
 (2n,x) is
the incomplete gamma
function and
(2n,x) is
the incomplete gamma
function and  is the
(complete) gamma function
(Ciotti 1991).
Useful Sérsic related expressions have been presented in
Ciotti (1991),
Simonneau & Prada
(2004)
and
Ciotti & Bertin
(1999),
while
Graham & Driver
(2005)
provide a detailed review of Sérsic's model plus associated
quantities and references to pioneers of this model.
is the
(complete) gamma function
(Ciotti 1991).
Useful Sérsic related expressions have been presented in
Ciotti (1991),
Simonneau & Prada
(2004)
and
Ciotti & Bertin
(1999),
while
Graham & Driver
(2005)
provide a detailed review of Sérsic's model plus associated
quantities and references to pioneers of this model.
The relation between the effective surface brightness (µe = -2.5log Ie) and the central surface brightness (µ0 = -2.5log I0) is given by the expression
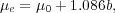 |
(2) |
where we have dropped the subscript n from the term bn for simplicity, while
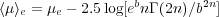 |
(3) |
gives the difference between the effective surface brightness and the mean effective surface brightness (⟨ µ ⟩e) within Re. Figure 2 shows the behaviour of the Sérsic model.
Uniting CCD data with wide and deep photographic images, Caon et al. (1990, 1993, 1994) revealed that the Sérsic R1 / n model provided a remarkably good description to the stellar distribution over a large radial range, down to surface brightnesses of ~ 28 B-mag arcsec-2, for the early-type galaxies brighter than MB = -18 mag in the Virgo cluster. This work was in essence an expansion of de Vaucouleurs & Capaccioli's (1979) study of NGC 3379 which is very well-fit with n = 4. Different galaxies were discovered by Caon et al. (1993) to be equally well fit, but required different values of n (see also Bertin et al. 2002).
Importantly, Caon et al. (1993) additionally showed that a correlation existed between stellar concentration, i.e. the Sérsic index n, and (model-independent) galaxy size that was not due to parameter coupling in the Sérsic model (see also Trujillo et al. 2001, their section 2). One of the commonly overlooked implications of this result is that R1/4, and similarly Petrosian (1976), magnitudes, sizes and surface brightnesses are systematically in error as a function of galaxy concentration (Graham et al. 2005; Hill et al. 2011). That is, application of a model which fails to adequately capture the range of stellar distributions will result in parameters which are systematically biased as a function of galaxy mass. For example, fitting an R1/4 model to elliptical galaxies which are actually described by an R1 / n model with n less than and greater than 4 will yield sizes and luminosities which are, respectively, greater than and less than the true value (e.g. Binggeli & Cameron 1991; Trujillo et al. 2001; Brown et al. 2003). Similarly, fitting an exponential model to bulges that are best described by an R1 / n model with n less than and greater than 1 will yield sizes and luminosities which are, respectively, greater than and less than the true value (e.g. Graham 2001). Obviously one does not want to fine tune their galaxy simulations to match scaling relations that contain systematic biases due to poor measurements, and observers are therefore busy fitting R1 / n models these days.
A good approximation to the internal-density profile associated with Sérsic's model, i.e. with its deprojection, was introduced by Prugniel & Simien (1997. Useful expressions for the dynamics, gravitational potential and forces of this model have been developed by Trujillo et al. (2002), Terzic & Graham (2005) and Terzic & Sprague (2007). Somewhat more complex than the early light-profile models, such expressions can, importantly, accommodate a range of concentrations, rather than only varying one scale radius and one scale density. Such a model is vital if one wishes to properly simulate and understand the mass spectrum of elliptical galaxies, whose Sérsic index n increases with stellar mass. While Graham & Driver's (2005) review stated that "No attempt has been made here to show the numerous scientific advances engendered via application of the R1 / n model", this article reveals how Sérsic's model, and the core-Sérsic model 0 (subsection 2.2), have become key in unifying and understanding the galaxies around us.
Like the majority of surface- and internal-density models from the last century, the Sérsic function is an empirical model created to match data rather than developed from theory, and as such we should be cautious before calling it a law. Attempts to find a physical explanation for de Vaucouleurs' model yielded results which helped to keep it in vogue. Dissipational models have long been touted for producing R1/4 profiles (e.g. Larson 1969, 1974), and in the 1980s papers based on dissipationless N-body simulations of a cold clumpy collapse or the merger of disc galaxies also claimed to finally produce R1/4 (and also Reynold) profiles (e.g. van Albada 1982; McGlynn 1984; Carlberg et al. 1986; Barnes 1988). However a closer inspection reveals clear departures from the R1/4 profile, with the simulated profiles better described by an R1 / n model with n < 4. Obviously their inability (or perhaps lack of desire, although see Farouki, Shapiro & Duncan 1983 whose non-homologous merger remnants were initially criticised by R1/4 aficionados) to create the range of stellar concentrations now observed in elliptical galaxies highlights a limitation of these early works. Nonetheless, these pioneering studies have led to N-body simulations by Nipoti et al. (2006) and Aceves et al. (2006) - and Farouki et al. (1983), whose results with a smaller force softening appeared years ahead of their time - have now recovered a range of Sérsic profile shapes for gravitational collapses in a dark matter halo and for disc galaxy mergers, respectively.
Given the empirical nature of Sérsic's R1 / n model, Hjorth & Madsen (1995) revealed how dissipationless merging and violent relaxation provided a physical explanation for the departure from the homologous R1/4 model. Other works have explained how the quasi-constant specific entropy associated with the post violent-relaxation stage of elliptical galaxies results in the observed mass-dependent range of stellar concentrations in elliptical galaxies (Gerbal et al. 1997; Lima Neto 1999; Márquez et al. 2001).
It does not seem too unreasonable to speculate that elliptical galaxies, whether built by near-monolithic collapse, collisions of disc galaxies, wet or dry mergers, appear to eventually experience the same force(s) of nature that results in their radial stellar distribution depending on the total stellar mass. That is, it may not matter how the mass was accumulated into an elliptical galaxy, once it becomes a dynamically-heated, bound stellar-system, it appears to eventually obey certain universal scaling relations (see section 3).
It is interesting to note that Sérsic actually introduced his model as a way to parameterise disc galaxies which he thought were comprised of differing ratios of a disc plus an R1/4-bulge. His model was not initially intended to fit elliptical galaxies, and as such it did not immediately threaten de Vaucouleurs' model. Credit for popularising the use of Sérsic's R1 / n model for approximating not only lenticular 9 bulge+disc galaxies but for describing pure elliptical galaxies resides largely with Massimo Capaccioli (e.g. Capaccioli 1985, 1987, 1989; Caon et al. 1993; D'Onofrio et al. 1994) 10. However, Davies et al. (1988) had also introduced this model for dwarf elliptical galaxies, while Sparks (1988) developed an early Gaussian seeing correction for this model, and Ciotti (1991) developed a number of associated expressions such as the velocity dispersion profile and a distribution function. The important quantification that Capaccioli and others provided is how the radial distribution of stars in elliptical galaxies, i.e. their concentration, varies with the size, luminosity and thus the mass of the elliptical galaxy (see also Cellone, Forte, & Geisler 1994; Vennik & Richter 1994; Young & Currie 1994, 1995; Graham et al. 1996; Karachentseva et al. 1996, Vennik et al. 1996). As we shall see in this article, the implications of this breakthrough have been dramatic, unifying what had previously been considered two distinct species of galaxy, namely dwarf and ordinary elliptical galaxies, previously thought to be described by an exponential and R1/4 model, respectively.
This review would be somewhat incomplete without a few words regarding
the connection between Sérsic's model and (simulated) dark matter
halos. While modified theories of gravity may yet make dark matter
redundant at some level, it is intriguing to note that the
Prugniel-Simien (1997)
internal-density model, developed to approximate
the deprojected form of Sérsic's R1 / n
model, additionally provides a very good representation of the
internal-density profiles of simulated dark matter halos.
Merritt et al. (2006)
revealed that it actually provides a better description than not
only the
Navarro, Frenk & White
(1997)
model but even a generalised
NFW model with an arbitrary inner profile slope
 .
.
Sérsic's former student, Navarrro, independently applied Sérsic's surface-density model to the internal-density profiles of simulated dark matter halos (Navarro et al. 2004; Merritt et al. 2005). Jaan Einasto (1965) had previously developed this same function as Sérsic to describe the internal-density profiles of galaxies. Rather than a universal profile shape, as advocated by Navarro et al. (1997), a range of simulated dark matter density profile shapes is now known to vary with the dark matter halo mass (Avila-Reese et al. 1999; Jing & Suto 2000; Merritt et al. 2005; Del Popolo 2010 and references therein). A number of useful expressions related to this "Einasto model", which has the same functional form as Sérsic's model but is applied to the internal rather than projected density profile, can be found in Cardone et al. (2005), Mamon & okas (2005) and Graham et al. (2006).
An apparent "bulge-halo conspiracy" between the radial distribution of
stellar mass and dark matter (after modification by baryons) has
arisen in recent years, such that elliptical galaxies reportedly have
total internal-density profiles
 (r)
described by power-laws
(Bertin & Stiavelli
1993;
Kochanek 1995;
Gavazzi et al. 2007;
Buote & Humphrey
2011).
These power-laws were originally claimed to be close to isothermal, such
that
(r)
described by power-laws
(Bertin & Stiavelli
1993;
Kochanek 1995;
Gavazzi et al. 2007;
Buote & Humphrey
2011).
These power-laws were originally claimed to be close to isothermal, such
that
 (r)
(r)
 r-2
(Koopmans et al. 2006,
2009;
Gavazzi et al. 2007).
Recent work now emphasises that only the sample average profile slope is
close to -2, and that a trend in slope with galaxy size exists
(Humphrey & Boute
2010;
Auger et al. 2010).
This is a developing field and it is worth noting that the analyses have
been confined to massive galaxies with velocity dispersions greater than
~ 175 km s-1, and thus with Sérsic indices n
r-2
(Koopmans et al. 2006,
2009;
Gavazzi et al. 2007).
Recent work now emphasises that only the sample average profile slope is
close to -2, and that a trend in slope with galaxy size exists
(Humphrey & Boute
2010;
Auger et al. 2010).
This is a developing field and it is worth noting that the analyses have
been confined to massive galaxies with velocity dispersions greater than
~ 175 km s-1, and thus with Sérsic indices n
 4
(Graham, Trujillo &
Caon 2001).
While the light profile shape changes dramatically as
the Sérsic index n increases from ~ 1 to ~ 4, there is not
such an obvious change in light profile shape from ~ 4 to higher values
of n (see Figure 2). The apparent
isothermal profiles of elliptical galaxies, and the alleged
"bulge-halo conspiracy", may turn out to be a by-product of sample selection
(i.e. choosing galaxies which have approximately the same structure).
It would be interesting to expand the Sloan Lens ACS (SLACS) Survey
(Bolton et al. 2006)
to a greater range than only bright early-type galaxies that are
approximately well fit with an R1/4 model, and to go
beyond the use of simple power-laws to describe the total mass density
profile once the data allows this. Two component mass models
(Prugniel-Simien+Einasto) to a range of galaxy masses await.
Claims that "early-type galaxies are structurally close to homologous" may
therefore be premature, as was the case for the distribution of stellar
light in elliptical
galaxies while the R1/4 model was thought to be a law.
4
(Graham, Trujillo &
Caon 2001).
While the light profile shape changes dramatically as
the Sérsic index n increases from ~ 1 to ~ 4, there is not
such an obvious change in light profile shape from ~ 4 to higher values
of n (see Figure 2). The apparent
isothermal profiles of elliptical galaxies, and the alleged
"bulge-halo conspiracy", may turn out to be a by-product of sample selection
(i.e. choosing galaxies which have approximately the same structure).
It would be interesting to expand the Sloan Lens ACS (SLACS) Survey
(Bolton et al. 2006)
to a greater range than only bright early-type galaxies that are
approximately well fit with an R1/4 model, and to go
beyond the use of simple power-laws to describe the total mass density
profile once the data allows this. Two component mass models
(Prugniel-Simien+Einasto) to a range of galaxy masses await.
Claims that "early-type galaxies are structurally close to homologous" may
therefore be premature, as was the case for the distribution of stellar
light in elliptical
galaxies while the R1/4 model was thought to be a law.
The centres of luminous galaxies have long been known to possess "cores", such that the surface-density profile flattens at the center (e.g. King & Minkowski 1966), and King & Minkowski (1972) remarked on the inability of the Reynold's and de Vaucouleurs' model to match these flattened cores in giant galaxies. Although King (1978) identified a number of galaxies thought to be well described by his model, using seeing-deconvolved ground-based images, Lauer (1983, 1984, 1985) analysed 14 galaxies with 'cores', ranging from 1.5-5.0 arcseconds in radius, revealing that they, like M87 (Young et al. 1978; Duncan & Wheeler 1980; Binney & Mamon 1982), were not exactly described by the King model which had a completely flat core. Similar conclusions, that cores existed but that they do not have flat inner surface brightness profiles, were also reported by Kormendy (1982, 1985a), creating the need for a new model to describe the stellar distribution in galaxies.
Nearly a decade later, the Hubble Space Telescope was flying and offered factors of a few improvement over the best image resolution achievable from the ground at that time. Not surprisingly, astronomers explored the centres of galaxies. In an effort to quantify these nuclear regions, after the abandonment of the King model and the lack of a flattened core in the R1/4 model, Crane et al. (1993), Ferrarese et al. (1994), Forbes et al. (1994) and Jaffe et al. (1994) used a double power-law model to describe the inner light profiles of large galaxies. Grillmair et al. (1994), Kormendy et al. (1994) and Lauer et al. (1995) also adopted a double-power-law model but one with an additional, fifth, parameter to control the sharpness of the transition. Their model, which they dubbed the "Nuker law" for describing the nuclear regions of galaxies (after excluding any apparent excess light), has the same functional form as the double power-law model presented by Hernquist (1990, his equation 43) to describe the internal-density of galaxies (Zhao 1996).
However, as noted by the above authors, these double power-law models were never intended to describe the entire radial extent of a galaxy's stellar distribution, and they provided no connection with the outer (R1/4-like) radial profile. This disconnection turned out to be their down fall. Due to the curved nature of the outer light profiles beyond the core, which were being fitted by the double power-law model's outer power-law, the five parameters of the Nuker model systematically changed as the fitted radial extent changed. This was first illustrated in a number of diagrams by Graham et al. (2003) who revealed that none of the Nuker model parameters were robust, and as such they could not provide meaningful physical quantities. For example, Trujillo et al. (2004) reported that the Nuker-derived core-radii were typically double, and up to a factor of five times larger, than the radius where the inner power-law core broke away from the outer R1/4-like profile - a result reiterated by Dullo & Graham (2011, in prep.). An additional problem was that these "break radii" were being identified in the so-called "power-law" galaxies that showed no evidence of a downward departure and flattening from the inward extrapolation of the outer R1/4-like profile. This situation arose because of the curved nature of what were actually Sérsic profiles. That is, the so-called "power-law" galaxies not only had no distinct "core" like the "core galaxies" do, but confusingly they do not even have power-law light profiles.
Given that Caon et al. (1993) and D'Onofrio et al. (1994) had established that the Sérsic function fits the brightness profiles of elliptical galaxies remarkably well over a large dynamic range (see the figures in Bertin et al. 2002), it is possible to confidently identify departures from these profiles that are diagnostic of galaxy formation. While in this and the following section we deal with partially-depleted cores - also referred to as "missing light" - in luminous galaxies (thought to be built from dissipationless mergers), the ensuing section addresses extra central light above the inward extrapolation of the outer Sérsic profile (found in galaxies that have experienced dissipation and star formation).
Building on the work of Caon et al. (1993), Graham et al. (2003) introduced the core-Sérsic model, which was applied in Trujillo et al. (2004. The model represents a modification to Sérsic's model such that it has an inner power-law core. This represented a dramatic change from what had gone before. While the Nuker team (e.g Kormendy et al. 1994; Lauer et al. 1995, 2005; Faber et al. 1997) were combining Nuker model parameters for the core with R1/4 model parameters for the main galaxy, Graham et al. (2003), Graham & Guzmán (2003), Balcells et al. (2003), Graham (2004) and Trujillo et al. (2004) advocated the measurement of core properties, excesses and deficits of light, measured relative to the outer Sérsic model.
For the first time, the core-Sérsic model provided an expression capable of unifying the nuclear regions of galaxies with their outer regions and also providing stable physical quantities 11. The model can be written as
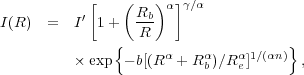 |
(4) |
where Rb denotes the break-radius separating the inner
power-law having logarithmic slope
 from the
outer Sérsic function.
The intensity Ib at the break-radius is such that
from the
outer Sérsic function.
The intensity Ib at the break-radius is such that
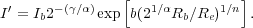 |
(5) |
The sixth and final parameter,
 , controls the sharpness
of the transition between the inner (power-law) and the outer
(Sérsic) regime - higher values of
, controls the sharpness
of the transition between the inner (power-law) and the outer
(Sérsic) regime - higher values of
 indicating a sharper
transition.
Figure 3 shows the core-Sérsic model (with
indicating a sharper
transition.
Figure 3 shows the core-Sérsic model (with
 = 100) applied to
NGC 3348.
= 100) applied to
NGC 3348.
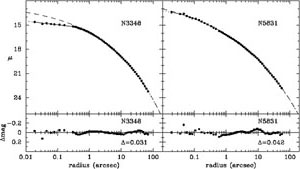 |
Figure 3. Left: Core-Sérsic model
(solid line) fit to the major-axis R-band light profile of
NGC 3348 (dots), with the dashed line showing the
associated Sérsic component. The inner depleted zone
corresponds to a stellar mass deficit of 3 × 108
M |
Terzic & Graham (2005) and Terzic & Sprague (2007) provide a number of expressions related to the potential, force and dynamics. 12 The core-Sérsic model is further discussed and used by Ferrarese et al. (2006a, b), Côté et al. (2006, 2007), Kawata, Cen & Ho (2007) and Ciotti (2009).
The collisional construction of galaxies from the merger of lesser galaxies is thought to be a common occurrence in the Universe. Coupled with the presence of a supermassive black hole (SMBH) at the heart of most galaxies (Wolfe & Burbidge 1970; Magorrian et al. 1998), dissipationless mergers were proposed by Begelman, Blandford & Rees (1980; see also Ebisuzaki, Makino, & Okumura 1991) to explain the depleted nuclei, i.e. the cores, observed in giant elliptical galaxies (e.g. King 1978, and references therein). It is thought that core-depletion is primarily due to the gravitational slingshot (Saslaw, Valtonen, & Aarseth 1974) effect that the coalescing SMBHs - from the pre-merged galaxies - have on stars while they themselves sink to the bottom of the potential well of the newly wed galaxy. 13
Theory predicts that the central mass deficit Mdef
should scale with
0.5N Mbh, where Mbh is the
final (merged) black hole mass and N the number of major "dry"
(i.e. gas free, dissipationless) mergers
(Milosavljevic &
Merritt 2001;
Merritt &
Milosavljevic 2005;
Merritt 2006a,
b).
Graham (2004)
used the core-Sérsic model to quantify the central deficit of
stars relative to the inward extrapolation of the outer Sérsic profile.
Figure 4 suggests that the luminous elliptical
galaxies sampled have experienced an average of 1 or 2 major dry
(i.e. dissipationless) mergers, a conclusion in agreement with select
 CDM models of
galaxy formation
(Haehnelt & Kauffmann
2002;
Volonteri et al. 2003).
CDM models of
galaxy formation
(Haehnelt & Kauffmann
2002;
Volonteri et al. 2003).
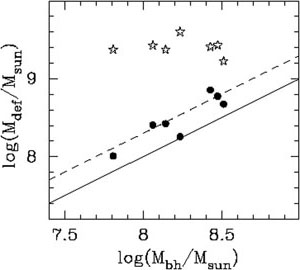 |
Figure 4. Central mass deficit for seven core galaxies derived using the core-Sérsic model (circles) and the Nuker model (stars) plotted against each galaxy's predicted central supermassive black hole mass. The solid and dashed line shows Mdef equal 1 and 2 Mbh, respectively. Figure adapted from Graham (2004). |
Quantification of the central stellar deficit relative to the inward extrapolation of the outer Sérsic profile has also been applied to bright Virgo cluster galaxies by Ferrarese et al. (2006a) and Côté et al. (2008) and with the exception of VCC 798 - a lenticular (bulge plus disc) galaxy - provides similar results. Of course when an outer disc exists, a core-Sérsic bulge plus disc fit is required, otherwise the disc will bias the Sérsic parameters. 14
While galaxies brighter than MB ~ -20.5 mag have partially depleted cores (e.g. Faber et al. 1997; Rest et al. 2001; Graham & Guzmán 2003), fainter galaxies often contain additional stellar components at their centres. Such excess nuclear light, above that of the underlying host galaxy, has long been known to exist (e.g. Smith 1935; Reaves 1956, 1977; Romanishin, Strom & Strom 1977) and was systematically studied by Binggeli et al. (1984), van den Bergh (1986) and Binggeli & Cameron (1991, 1993) in a number of dwarf elliptical galaxies. As far back as Larson (1975) it was known that simulations containing gas can account for these dense nuclear star clusters; clusters which became easier to detect with the Hubble Space Telescope (e.g. Carollo, Stiavelli & Mack 1998).
For many years it was common practice to simply exclude these additional nuclear components from the analysis of the galaxy light profile (e.g. Lauer et al. 1995; Byun et al. 1996; Rest et al. 2001; Ravindranath et al. 2001). Using HST data, Graham & Guzmán (2003) simultaneously modelled the host galaxy and the additional nuclear component with the combination of a Sérsic function for the host galaxy plus a Gaussian function for the nuclear star cluster. As we will see in section 4, they also showed that the lenticular galaxies in their early-type galaxy sample could be modelled via a Sérsic-bulge plus an exponential-disc plus a Gaussian-(star cluster) decomposition of their light profile - as done by Wadadekar et al. (1999) with ground-based images. Many other studies have since modeled the nuclear star clusters seen in HST images, see Figure 5, with the combination of a nuclear component plus a Sérsic host galaxy (e.g. Grant et al. 2005; Côté et al. 2006; Ferrarese et al. 2006a; Graham & Spitler 2009).
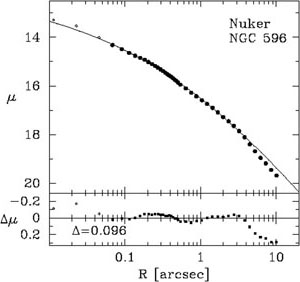 |
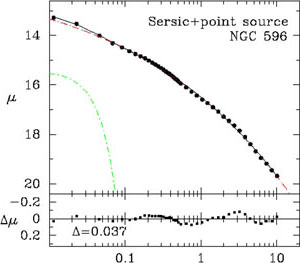 |
Figure 5. Left: 5-parameter Nuker model fit to the V-band light-profile of the nucleated galaxy NGC 596 after excluding the inner three data points (Lauer et al. 2005). Right: 3-parameter Sérsic model plus 2-parameter point-source (Gaussian) fit to the same light profile of NGC 596. With the same number of parameters, this model fits both the inner, intermediate, and outer light-profile. Figure from Dullo & Graham (2011, in prep.). |
|
While Graham & Guzmán (2003) and Côté et al. (2006) found that some nuclear star clusters could actually be resolved, it is not yet established what mathematical function best describes their radial distribution of stars. The closest example we have to study is of course the 30 million solar mass nuclear star cluster at the centre of the Milky Way (Launhardt et al. 2002). Graham & Spitler (2009) provided what may have been the first ever analysis after allowing for the significant contamination from bulge stars. Although they found that the cluster could be well described by a Sérsic index with n = 3 (see Figure 6, it remains to be tested how well a King model can describe the data, or at least the old stellar population known to have a core (e.g. Genzel et al. 1996). The excess nuclear light in M32 has also been well fit with an n = 2.3 Sérsic function (Graham & Spitler) but this too may yet be better described by a King model. What is apparent is that neither the underlying bulge nor the nuclear component are described by a power-law. Theories which form or assume such power-law cusps appear to be at odds with current observations.
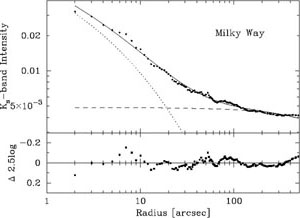 |
Figure 6. Uncalibrated, 2MASS, Ks-band intensity profile from the centre of the Milky Way, taken from Schödel et al. (2009, their Figure 2). The nuclear star cluster is modelled with a Sérsic function with n = 3 (dotted curve) and the underlying host bulge with an exponential function (Kent et al. 1991) that has an effective half-light radius of ~ 4.5 degrees (e.g. Graham & Driver 2007) and is therefore basically a horizontal line. One parsec equals 25 arcseconds. Figure from Graham & Spitler (2009). |
This section shall be somewhat cursory given R.Bower's detailed chapter on clusters and the intracluster medium in this volume.
Brightest cluster galaxies (BCGs), residing close to or at the centres of large galaxy clusters, have long been recognised as different from less luminous elliptical galaxies: their light profiles appear to have excess flux at large radii (e.g. Oemler 1976; Carter 1977; van den Bergh 1977; Lugger 1984; Schombert et al. 1986). However, before exploring this phenomenon, it is important to recall that the light profiles of large galaxies have Sérsic indices n greater than 4 (e.g. Caon et al. 1993; Graham et al. 1996). 15. Subsequently, at large radii in big elliptical galaxies, there will be excess flux above that of an R1/4 model fit to some limited inner radial range.
An initially puzzling result from the Sloan Digital Sky Survey (SDSS; York et al. 2000) survey was the lack of light profiles with Sérsic n > 5-6 (Blanton et al. 2005a). This was however soon resolved when Blanton et al. (2005b), Mandelbaum et al. (2005) and Lisker (2005, 2006b, 2007) pointed out a serious sky-subtraction problem with the early SDSS Photometric Pipeline (photo: Ivezic et al. 2004). The sky-value to be subtracted from each galaxy had been measured to close to the galaxy in question, and because galaxies with large Sérsic indices possess rather extended light-profiles, their outer galaxy light was actually measured and then subtracted from these galaxies. As a result, the high Sérsic index light-profiles were erroneously erased and missed from the SDSS. This resulted in the R1/4 model appearing to provide good fits to bright elliptical galaxies, and consequently a series of papers based on structurally biased radii, magnitudes and surface brightnesses.
Bearing in mind that large elliptical galaxies have high Sérsic indices, it is important to distinguish between (i) an inadequacy of the R1/4 model to describe what is actually a single R1/n profile, and (ii) a distinct physical component such as an envelope of diffuse halo light surrounding a central galaxy. Early quantitative photometry of cD galaxies (supergiant D galaxies: e.g. Matthews et al. 1964; Morgan & Lesh 1965) suggested the presence of an inner R1/4 spheroid plus an outer exponential corona (de Vaucouleurs 1969; de Vaucouleurs & de Vaucouleurs 1970). One should however question if this outer corona is a distinct entity or not. To answer this in the affirmative, astronomers can point to how the light profiles can display inflections marking the transition from BCG light to intracluster light. Gonzalez et al. (2005) additionally showed that the inflection in the light profiles of many BCGs was also associated with an a change in the ellipticity profile, signalling the switch from BCG light to intracluster light.
Gonzalez et al. (2005)
and
Zibetti et al. (2005)
chose to model their BCG
sample using an R1/4 + R1/4 model to
describe the inner galaxy plus
the outer halo light. However, given that elliptical galaxies are better
described by the R1/n model, and the desire to
measure the actual concentration of halos rather than assign a fixed
R1/4 profile,
Seigar et al. (2007)
fitted an R1/n + R1/n
model to the light profiles of five
BCGs. Not surprisingly, they found that the R1/4 +
R1/4 model was not
the optimal representation. An R1/n-galaxy plus
an exponential-halo
model was found to provide the optimal fit in three instances, with an
additional galaxy having no halo detected. The associated galaxy-to-halo
luminosity ratios can be found there. This re-revelation of an
exponential model, rather
than an R1/4 model, describing the halo has since been
confirmed by
Pierini et al. (2008.
Intriguing is that the halo does not trace the
NFW-like dark-matter halo density profiles produced in
 CDM
simulations (section 2.1.1). Stellar halos around
non-BCG galaxies have also now been reported to display an exponential
radial distribution (e.g.
Gadotti 2011;
Tal & van Dokkum
2011).
CDM
simulations (section 2.1.1). Stellar halos around
non-BCG galaxies have also now been reported to display an exponential
radial distribution (e.g.
Gadotti 2011;
Tal & van Dokkum
2011).
6 King (1962) also noted that his model failed to fit the inner region of bright elliptical galaxies. Back.
7 The Wilson (1975) and Elson (1987) model are also useful for describing globular clusters. Back.
8 Ellipticity gradients result in a different Sérsic index for the major- and minor-axis, as noted by Caon et al. (1993) and later quantified by Ferrari et al. (2004. Back.
9 This term was introduced by Knox Shaw (1915) and Reynolds (1920) in their galaxy classification scheme. Back.
10 It is worth noting that D'Onofrio (2001) re-modelled the Virgo and Fornax 2-component lenticular galaxies with an R1 / n-bulge plus an exponential disc (see section 4. Back.
11 The core-Sérsic, and also Sérsic, model provide robust parameters beyond the core if one has sufficient data to sample the curvature in the light profile, in practice this requires radial data out to ~ 1Re. Back.
12 The complex nature of this model has resulted in the appearance of alternate expressions, e.g. Spergel (2010, see his figure 3). Back.
13 The presence of FUV - NUV colour gradients in core galaxies such as NGC 1399 suggests that they may not have been built from major, dry merger events (Carter et al. 2011). Additionally, the globular cluster specific frequency in core galaxies may be at odds with core-galaxy formation through equal-mass merger events because the fainter, intermediate luminosity elliptical galaxies may have lower specific frequencies (Harris & van den Bergh 1981). Alternative ideas for core-formation in giant galaxies have been proposed: Boylan-Kolchin et al. 2004; Nipoti et al. 2006; Martizzi et al. 2011. Back.
14 Trujillo et al. (2004) and Graham (2004) intentionally excluded lenticular galaxies from their publication because it was felt that the community were not yet ready for an 8-parameter model (6 core-Sérsic plus 2 exponential disc parameters). Intriguingly, VCC 798 resides near the 1-to-1 line in Figure 4 when an exponential-disc plus (core-Sérsic)-bulge fit is performed (Graham, unpublished work). Back.
15 As n

 ,
the Sérsic model can be approximated by a power-law (see
Graham & Driver
2005).
Back.
,
the Sérsic model can be approximated by a power-law (see
Graham & Driver
2005).
Back.