We studied the modelling of stochasticity for stellar populations. Such stochasticity is intrinsic in the modelling in that we do not directly know the individual stars in a generic stellar system. We must use probability distributions and assign probabilities for the presence of each individual star. The only possible result of the modelling is a probabilistic description including all possible situations.
The input probability distribution is the stellar birth rate
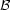(m0,
t, Z), which represents the probability that an individual
star was born with a given initial mass m0 at a given
time t with a given metallicity Z. This probability
distribution is modified by the transformations provided by stellar
evolution theory and evaluated at different times
tmod. The resulting distribution, the stellar
luminosity function, represents the probability that a star had a given
luminosity set (e.g. a set of colours or wavelengths),
ℓ1 ... ℓn, at a given time.
The probability distribution of the integrated luminosity of a system
with 
stars can be obtained
directly from the stellar luminosity function in an exact way via a
self-convolution process. It can also be obtained from a set of
nsim Monte Carlo simulations. Finally, it can be
described as a function of parameters of the distribution (mean,
variance, skewness, and kurtosis) that is related to the stellar
luminosity function by simple scale relations. Standard synthesis models
use a parametric description, although, with some exceptions, they only
compute the mean value of the distribution.
Hence, the results of standard (parametric) modelling can be used in any
situation, including = 1
(i.e. CMDs), as long as we understand that it is only a mean value of
possible luminosities. However, mean values are not useful unless we
know the shape of the distribution. In the most optimistic case, for
large
values, the distribution
is Gaussian and is hence defined by the mean and variance of each
luminosity, and the covariance between the different luminosities. The
value of when this
Gaussian regime is reached can be obtained by analysis of the skewness
and kurtosis of the stellar luminosity function.
Monte Carlo modelling (or the self-convolution process) is a useful
approach outside the Gaussian regime. However, Monte Carlo simulations
can only be fully understood if they are analysed with a parametric
description of the possible probability distributions. In addition,
Monte Carlo simulations are an ideal tool for including constraints in
fine-tuned modelling of particular objects or situations. A drawback is
that large sets of Monte Carlo simulations implicitly include additional
priors, such as the distribution of ages or
values. Such priors must
be chosen carefully in any application inferring physical parameters
from observations since possible inferences depend on them according to
the Bayes theorem. Finally, it is not possible to evaluate the
reliability of Monte Carlo simulations without explicit knowledge of the
number of simulations nsim,
, and all the assumed priors.
The fact that even in the most optimistic case of
= ∞, the
distribution of integrated luminosities is Gaussian (where the
parameters of the Gaussian distribution depend on size, age, and
metallicity) has major implications for the use of synthesis models to
obtain inferences. The principal one is that each model and wavelength
has its own physical scatter. This defines a metric of fitting for each
model (i.e. not all wavelengths are equivalent in the fit and they must
be weighted according their own physical scatter). An advantage of the
use of such fitting metrics is that it breaks degeneracies in physical
properties, such as age-metallicity degeneracy. A second implication is
that we can obtain physical information from observed scatter.
Finally, throughout the paper we explored additional implications and applications of the probabilistic modelling of stellar populations. Most of them are only tentative ideas, but they increase the predictive power of synthesis models and provide more accurate inferences of physical parameters from observational data.
Addendum after publication (only in astro-ph version): After the publication of this review, appear in the literature an additional paper dealing with modeling stellar populations by means of Monte Carlo simulations by Anders et al. (2013). Models results and programs related with that work will available at: http://data.galev.org/models/anders13.
Acknowledgements
My work is supported by MICINN (Spain) through AYA2010-15081 and AYA2010-15196 programmes. I acknowledge the development of TopCat software (Taylor 2005) since it helped me greatly in obtaining Figs. 5 and 11. This review compiles the efforts of many years of thinking and working with stellar population models and stochasticity, and it would not have been possible without the collaboration of Valentina Luridiana. I also acknowledge Alberto Buzzoni and Steve Shore for suggestions, comments and discussions on the modelling and applications of these ideas, most of then outlined here. I acknowledge Roberto and Elena Terlevich, David Valls Gabaud, Sandro Bressan, Mercedes Molla, Jesús Maíz Apellaniz, and Angel Bongiovani for useful discussion. Also, I acknowledge Carma Gallart and J. Maíz Appelaniz for providing me some figures for this review, and Sally Oey for her feedback and to give me the opportunity of write this review. Finally, I acknowledge Nuno and Carlos (twins), Dario and Eva who show experimentally that Nature fluctuates around theoretical expectations (no-twins), and that such fluctuations make life (and science) more interesting.