3. GMC FORMATION

We now turn to the question of how GMCs form. The main mechanisms that have been proposed, which we discuss in detail below, are converging flows driven by stellar feedback or turbulence (Section 3.1), agglomeration of smaller clouds (Section 3.2), gravitational instability (Section 3.3) and magneto-gravitational instability (Section 3.4), and instability involving differential buoyancy (Section 3.5). All these mechanisms involve converging flows, i.e., ∇ ⋅ u < 0, where u is the velocity, which may be continuous or intermittent. Each mechanism however acts over different sizes and timescales, producing density enhancements of different magnitudes. Consequently, different mechanisms may dominate in different environments, and may lead to different cloud properties. In addition to these physical mechanisms for gathering mass, forming a GMC involves a phase change in the ISM, and this too may happen in a way that depends on the large-scale environment (Section 3.6).

Two processes that we will not consider as cloud formation mechanisms are thermal instabilities (TI, Field 1965) and magneto-rotational instabilities (MRI, Balbus and Hawley 1991). Neither of these by themselves are likely to form molecular clouds. TI produces the cold (100 K) atomic component of the ISM, but the cloudlets formed are ~ pc in scale, and without the shielding provided by a large gas column this does not lead to 10-20 K molecular gas. Furthermore, TI does not act in isolation, but interacts with all other processes taking place in the atomic ISM (Vázquez-Semadeni et al. 2000, Sánchez-Salcedo et al. 2002, Piontek and Ostriker 2004, Kim et al. 2008). Nevertheless the formation of the cold atomic phase aids GMC formation by enhancing both shock compression and vertical settling, as discussed further in Section 3.2. The MRI is not fundamentally compressive, so again it will not by itself lead to GMC formation, although it can significantly affect the development of large-scale gravitational instabilities that are limited by galactic angular momentum (Kim et al. 2003). MRI or TI may also drive turbulence (Koyama and Inutsuka 2002, Kritsuk and Norman 2002, Kim et al. 2003, Piontek and Ostriker 2005, Piontek and Ostriker 2007, Inoue and Inutsuka 2012), and thereby aid cloud agglomeration and contribute to converging flows. However, except in regions with very low SFR, the amplitudes of turbulence driven by TI and MRI are lower than those driven by star formation feedback.

3.1. Localized Converging Flows

Stellar feedback processes such as the expansion of H ii regions (Bania and Lyon 1980, Vazquez-Semadeni et al. 1995, Passot et al. 1995) and supernova blast waves (McCray and Kafatos 1987, Gazol-Patiño and Passot 1999, de Avillez 2000, de Avillez and Mac Low 2001, de Avillez and Breitschwerdt 2005, Kim et al. 2011, Ntormousi et al. 2011) can drive converging streams of gas that accumulate to become molecular clouds, either in the Galactic plane or above it, or even after material ejected vertically by the local excess of pressure due to the stars/supernovae falls back into the plane of the disk. Morphological evidence for this process can be found in large-scale extinction maps of the Galaxy (see Fig. 4), and recent observations in both the Milky Way and the LMC, confirm that MCs can be found at the edges of supershells (Dawson et al. 2011, Dawson et al. 2013).

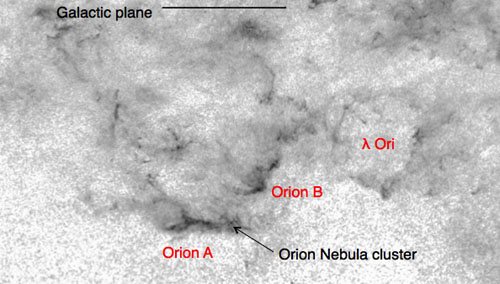Figure 4. Extinction map towards the Orion-Monoceros molecular complex. Different features are located at different distances, but at the mean distance of Orion, the approximate size of the A and B clouds, as well as the Ori ring, is of the order of 50 pc. Note the presence of shells at a variety of scales, presumably due to OB stars and/or supernovae. The Ori ring surrounds a 5 Myr old stellar cluster, and it is thought to have been produced by a supernova (data from Rowles and Froebrich 2009, as adapted by L. Hartmann (2013, in preparation)).

Locally - on scales up to ~ 100 pc - it is likely that these processes play a dominant role in MC formation, since on these scales the pressure due to local energy sources is typically P / k_B ~ 10⁴ K cm^-3, which exceeds the mean pressure of the ISM in the Solar neighborhood (Draine 2011). The mass of MCs created by this process will be defined by the mean density ₀ and the velocity correlation length, L of the converging streams; L is less than the disk scale height H for local turbulence. For Solar neighborhood conditions, where there are low densities and relatively short timescales for coherent flows, this implies a maximum MC mass of a few times 10⁴ M. Converging flows driven by large-scale instabilities can produce higher-mass clouds (see below).

A converging flow it not by itself sufficient to form a MC; the detailed initial velocity, density, and magnetic field structure must combine with TI to produce fast cooling (e.g., McCray et al. 1975, Bania and Lyon 1980, Vazquez-Semadeni et al. 1995, Hennebelle and Pérault 1999, Koyama and Inutsuka 2000, Audit and Hennebelle 2005, Heitsch et al. 2006, Vázquez-Semadeni et al. 2007). This allows rapid accumulation of cold, dense atomic gas, and thus promotes molecule formation. The accumulation of gas preferentially along field lines (perhaps due to magneto-Jeans instability - see Section 3.4) also increases the mass to flux ratio, causing a transition from subcritical gas to supercritical (Hartmann et al. 2001, Vázquez-Semadeni et al. 2011). Thus the accumulation of mass from large-scale streams, the development of a molecular phase with negligible thermal support, and the transition from magnetically subcritical to supercritical all happen essentially simultaneously, at a column density of ~ 10²¹cm^-2; (Hartmann et al. 2001, see also Section 3.6), allowing simultaneous molecular cloud and star formation.

This mechanism for GMC formation naturally explains the small age spread observed in MCs near the Sun (see Section 2.5), since the expected star formation timescale in these models is the thickness of the compressed gas (~ few pc) divided by the inflow velocity (~ few km s^-1). In addition to the overall age spread, the shape of the stellar age distribution produced by this mechanism is consistent with those observed in nearby MCs: most of the stars have ages of 1-3 Myr, and only few older. While some of these regions may be contamination by non-members (Hartmann 2003), the presence of some older stars might be the result of a few stars forming prior to the global but hierarchical and chaotic contraction concentrates most of the gas and forms most of the stars (Hartmann et al. 2012). This model is also consistent with the observed morphology of Solar neighborhood clouds, since their elongated structures would naturally result from inflow compression.

3.2. Spiral-Arm Induced Collisions

While localized converging flows can create clouds with masses up to ~ 10⁴ M, most of the molecular gas in galaxies is found in much larger clouds (Section 2.3). Some mechanism is required to either form these large clouds directly, or to induce smaller clouds to agglomerate into larger ones. Although not yet conclusive, there is some evidence of different cloud properties in arms compared to inter-arm regions, which could suggest different mechanisms operating (Colombo et al., submitted). It was long thought that the agglomeration of smaller clouds could not work because, for clouds moving with observed velocity dispersions, the timescale required to build a 10⁵ - 10⁶ M cloud would be > 100 Myr (Blitz and Shu 1980). However in the presence of spiral arms, collisions between clouds become much more frequent, greatly reducing the timescale (Casoli and Combes 1982, Kwan and Valdes 1983, Dobbs 2008). Fig. 5 shows a result from a simulation where GMCs predominantly form from spiral arm induced collisions. Even in the absence of spiral arms, in high surface density galaxies (Tasker and Tan 2009) find that collisions are frequent enough (every ~ 0.2 orbits) to influence GMC properties, and possibly star formation (Tan 2000). The frequency and success of collisions is enhanced by clouds' mutual gravity (Kwan and Valdes 1987, Dobbs 2008), but is suppressed by magnetic fields (Dobbs and Price 2008).

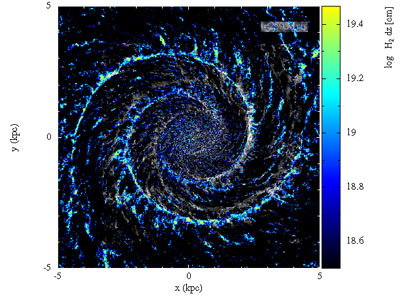Figure 5. A snapshot is shown from a simulation of the gas in a spiral galaxy, including a fixed sprial potential, gas heating and cooling, self gravity and stellar feedback (from Dobbs and Pringle 2013). The GMCs in this simulation predominanlty form by cloud-cloud collisions in the spiral arms. The black and white color scheme shows the total gas column density, whilst the blue-yellow scheme shows the H2 fraction integrated through the disc.

This mechanism can explain a number of observed features of GMCs. Giant molecular associations in spiral arms display a quasi-periodic spacing along the arms (Elmegreen and Elmegreen 1983, Efremov 1995), and Dobbs (2008) show that this spacing can be set by the epicyclic frequency imposed by the spiral perturbation, which governs the amount of material which can be collected during a spiral arm passage. A stronger spiral potential produces more massive and widely spaced clouds. The stochasticity of cloud-cloud collisions naturally produces a powerlaw GMC mass function (Field and Saslaw 1965, Penston et al. 1969, Taff and Savedoff 1973, Handbury et al. 1977, Kwan 1979, Hausman 1982, Tomisaka 1984), and the powerlaw indices produced in modern hydrodynamic simulations agree well with observations (Dobbs 2008, Dobbs et al. 2011a, Tasker and Tan 2009), provided the simulations also include a subgrid feedback recipe strong enough to prevent runaway cloud growth (Dobbs et al. 2011a, Hopkins et al. 2011). A third signature of either local converging flows or agglomeration is that they can produce clouds that are counter-rotating compared to the galactic disk (Dobbs 2008, Dobbs et al. 2011a, Tasker and Tan 2009), consistent with observations showing that retrograde clouds are as common as prograde ones (Blitz 1993, Phillips 1999, Rosolowsky et al. 2003, Imara and Blitz 2011, Imara et al. 2011). Clouds formed by agglomeration also need not be gravitationally bound, although, again, stellar feedback is necessary to maintain an unbound population (Dobbs et al. 2011b).

3.3. Gravitational Instability

An alternative explanation for massive clouds is that they form in a direct, top-down manner, and one possible mechanism for this to happen is gravitational instability. Axisymmetric perturbations in single-phase infinitesimally thin gas disks with effective sound speed c_eff, surface density , and epicyclic frequency can occur whenever the Toomre parameter Q ≡ c_eff / ( G ) < 1. For the nonaxisymmetric case, however, there are no true linear (local) instabilities because differential rotation ultimately shears any wavelet into a tightly wrapped trailing spiral with wavenumber k∝ t in which pressure stabilization (contributing to the dispersion relation as k² c_eff²) is stronger than self-gravity (contributing as -2 G _gas|k|). Using linear perturbation theory, Goldreich and Lynden-Bell (1965b) were the first to analyze the growth of low-amplitude shearing wavelets in gaseous disks; the analogous "swing amplification" process for stellar disks was studied by Julian and Toomre (1966). Spiral-arm regions, because they have higher gaseous surface densities, are more susceptible than interarm regions to self-gravitating fragmentation, and this process has been analyzed using linear theory (e.g., Elmegreen 1979, Balbus and Cowie 1985, Balbus 1988). Magnetic effects are particularly important in spiral-arm regions because of the reduced shear compared to interarm regions; this combination leads to a distinct process termed the magneto-Jeans instability (MJI; see Section 3.4).

Nonaxisymmetric disturbances have higher Q thresholds for growth (i.e., amplification is possible at lower ) than axisymmetric disturbances. Because the instabilities are nonlinear, numerical simulations are required to evaluate these thresholds. Kim and Ostriker (2001) found, for local thin-disk simulations and a range of magnetization, that the threshold is at Q = 1.2-1.4. Vertical thickness of the disk dilutes self-gravity, which tends to reduce the critical Q below unity, but magnetic fields and the contribution of stellar gravity provide compensating effects, yielding Q_crit ~ 1.5 (Kim et al. 2002, 2003, Kim and Ostriker 2007, Li et al. 2005).

In the absence of a pre-existing "grand design" stellar spiral pattern, gravitational instability in the combined gas-star disk can lead to flocculent or multi-armed spirals, as modeled numerically by e.g., Li et al. (2005), Kim and Ostriker (2007), Robertson and Kravtsov (2008), Tasker and Tan (2009), Dobbs et al. (2011a), Wada et al. (2011), Hopkins (2012). In cases where a grand design is present (e.g., when driven by a tidal encounter), gas flowing through the spiral pattern supersonically experiences a shock, which raises the density and can trigger gravitational collapse (Roberts 1969); numerical investigations of this include e.g., Kim and Ostriker (2002), Kim and Ostriker (2006), Shetty and Ostriker (2006), Dobbs et al. (2012); see also Section 3.4 for a discussion of magnetic effects.

Clouds formed by gravitational instabilities in single-phase gas disks typically have masses ~ 10 times the two-dimensional Jeans mass M_J,2D = c_eff⁴ / (G² ) ~ 10⁸ M(c_eff / 7 km s^-1)⁴ ( / M pc^-2)^-1. The gathering scale for mass is larger than the 2D Jeans length L_J,2D = c_eff² / (G ) in part because the fastest-growing scale exceeds L_J,2D even for infinitesimally-thin disks, and this increases for thick disks; also, the cloud formation process is highly anisotropic because of shear. At moderate gas surface densities, < 100 M pc^-2, as found away from spiral-arm regions, the corresponding masses are larger than those of observed GMCs when c_eff ~ 7 km s^-1, comparable to large-scale mean velocity dispersions for the atomic medium. The absence of such massive clouds is consistent with observations indicating that Q values are generally above the critical threshold (except possibly in high redshift systems), such that spiral-arm regions at high and/or processes that reduce c_eff locally are required to form observed GMCs via self-gravitating instability. While many analyses and simulations assume a single-phase medium, the diffuse ISM from which GMCs form is in fact a multi-phase medium, with cold clouds surrounded by a warmer intercloud medium. The primary contribution to the effective velocity dispersion of the cold medium is turbulence. This turbulence can dissipate due to cloud-cloud collisions, as well as large-scale flows in the horizontal direction, and flows towards the midplane from high latitude. Turbulent dissipation reduces the effective pressure support, allowing instability at lower (Elmegreen (2011)). In addition, the local reduction in c_eff enables gravitational instability to form lower mass clouds. Simulations that include a multi-phase medium and/or feedback from star formation (which drives turbulence and also breaks up massive GMCs) find a broad spectrum of cloud masses, extending up to several × 10⁶ M (e.g., Wada et al. 2000, Shetty and Ostriker 2008, Tasker and Tan 2009, Dobbs et al. 2011a, Hopkins 2012).

3.4. Magneto-Jeans Instability

In magnetized gas disks, another process, now termed the magneto-Jeans instability (MJI), can occur. This was first investigated using linear perturbation theory for disks with solid-body rotation by Lynden-Bell (1966), and subsequently by Elmegreen (1987), Gammie (1996), and Kim and Ostriker (2001) for general rotation curves. MJI occurs in low-shear disks at any nonzero magnetization, whereas swing amplification (and its magnetized variants) described in Section 3.3 requires large shear. In MJI, magnetic tension counteracts the Coriolis forces that can otherwise suppress gravitational instability in rotating systems, and low shear is required so that self-gravity takes over before shear increases k to the point of stabilization. Kim and Ostriker (2001) and Kim et al. (2002) have simulated this process in uniform, low-shear regions as might be found in inner galaxies.

Because low shear is needed for MJI, it is likely to be most important either in central regions of galaxies or in spiral arms (Elmegreen (1994)), where compression by a factor / ₀ reduces the local shear as dln / d lnR ~ / ₀ - 2. Given the complex dynamics of spiral arm regions, this is best studied with MHD simulations (Kim and Ostriker 2002, 2006, Shetty and Ostriker 2006), which show that MJI can produce massive, self-gravitating clouds either within spiral arms or downstream, depending on the strength of the spiral shock. Clouds that collapse downstream are found within overdense spurs. The spiral arms maintain their integrity better in magnetized models that in comparison unmagnetized simulations. Spacings of spiral-arm spurs formed by MJI are several times the Jeans length c_eff² / (G _arm) at the mean arm gas surface density _arm, consistent with observations of spurs and giant H ii regions that form "beads on a string" in grand design spirals (Elmegreen and Elmegreen 1983, La Vigne et al. 2006). The masses of gas clumps formed by MJI are typically ~ 10⁷ M in simulations with c_eff = 7 km s^-1, comparable to the most massive observed giant molecular cloud complexes and consistent with expectations from linear theory. Simulations of MJI in multiphase disks with feedback-driven turbulence have not yet been conducted, so there are no predictions for the full cloud spectrum.

3.5. Parker Instability

A final possible top-down formation mechanism is Parker instability, in which horizontal magnetic fields threading the ISM buckle due to differential buoyancy in the gravitational field, producing dense gas accumulations at the midplane. Because the most unstable modes have wavelengths ~ (1-2)2 H, where H is the disk thickness, gas could in principle be gathered from scales of several hundred pc to produce quite massive clouds (Mouschovias 1974, Mouschovias et al. 1974, Blitz and Shu 1980). However, Parker instabilities are self-limiting (e.g., Matsumoto et al. 1988), and in single-phase media saturate at factor of few density enhancements at the midplane (e.g., Basu et al. 1997, Santillán et al. 2000, Machida et al. 2009). Simulations have also demonstrated that three-dimensional dynamics, which enhance reconnection and vertical magnetic flux redistribution, result in end states with relatively uniform horizontal density distributions (e.g., Kim et al. 1998, Kim et al. 2003). Some models suggest that spiral arm regions may be favorable for undular modes to dominate over interchange ones (Franco et al. 2002), but simulations including self-consistent flow through the spiral arm indicate that vertical gradients in horizontal velocity (a consequence of vertically-curved spiral shocks) limit the development of the undular Parker mode (Kim and Ostriker 2006). While Parker instability has important consequences for vertical redistribution of magnetic flux, and there is strong evidence for the formation of magnetic loops anchored by GMCs in regions of high magnetic field strength such as the Galactic Center (Fukui et al. 2006, Torii et al. 2010), it is less clear if Parker instability can create massive, highly overdense clouds.

For a medium subject to TI, cooling of overdense gas in magnetic valleys can strongly enhance the density contrast of structures that grow by Parker instability (Kosinski and Hanasz 2007, Mouschovias et al. 2009). However, simulations to date have not considered the more realistic case of a pre-existing cloud / intercloud medium in which turbulence is also present. For a non-turbulent medium, cold clouds could easily slide into magnetic valleys, but large turbulent velocities may prevent this. In addition, whatever mechanisms drive turbulence may disrupt the coherent development of large-scale Parker modes. An important task for future modeling of the multiphase, turbulent ISM is to determine whether Parker instability primarily re-distributes the magnetic field and alters the distribution of low-density coronal gas, or if it also plays a major role in creating massive, bound GMCs near the midplane.

3.6. Conversion of H to H₂, and C⁺ to CO

Thus far our discussion of GMC formation has focused on the mechanisms for accumulating high density gas. However, the actual observable that defines a GMC is usually CO emission, or in some limited cases other tracers of H₂ (e.g., Bolatto et al. 2011). Thus we must also consider the chemical transition from atomic gas, where the hydrogen is mostly H i and carbon is mostly C⁺, to molecular gas characterized by H₂ and CO. The region over which this transition occurs is called a photodissociation or photon-dominated region (PDR). H₂ molecules form (primarily) on the surfaces of dust grains, and are destroyed by resonant absorption of Lyman- and Werner-band photons. The equilibrium H₂ abundance is controlled by the ratio of the far ultraviolet (FUV) radiation field to the gas density, so that H₂ becomes dominant in regions where the gas is dense and the FUV is attenuated (van Dishoeck and Black 1986, Black and van Dishoeck 1987, Sternberg 1988, Krumholz et al. 2008, 2009a, Wolfire et al. 2010). Once H₂ is abundant, it can serve as the seed for fast ion-neutral reactions that ultimately culminate in the formation of CO. Nonetheless CO is also subject to photodissociation, and it requires even more shielding than H₂ before it becomes the dominant C repository (van Dishoeck and Black 1988).

The need for high extinction to form H₂ and CO has two important consequences. One, already alluded to in Section 2, is that the transition between H i and H₂ is shifted to higher surface densities in galaxies with low metallicity and dust abundance and thus low extinction per unit mass (Fumagalli et al. 2010, Bolatto et al. 2011, Wong et al. 2013). A second is that the conversion factor X_CO between CO emission and H₂ mass increases significantly in low metallicity galaxies (Bolatto et al. 2013, and references therein), because the shift in column density is much greater for CO than for H₂. CO and H₂ behave differently because self-shielding against dissociation is much stronger for H₂ than for CO, which must rely on dust shielding (Wolfire et al. 2010). As a result, low metallicity galaxies show significant CO emission only from high-extinction peaks of the H₂ distribution, rather than from the bulk of the molecular material.

While the chemistry of GMC formation is unquestionably important for understanding and interpreting observations, the connection between chemistry and dynamics is considerably less clear. In part this is due to numerical limitations. At the resolutions achievable in galactic-scale simulations, one can model H₂ formation only via subgrid models that are either purely analytic (e.g., Krumholz et al. 2008, 2009a, 2009b, McKee and Krumholz 2010, Narayanan et al. 2011, 2012, Kuhlen et al. 2012, Jaacks et al. 2013) or that solve the chemical rate equations with added "clumping factors" that are tuned to reproduce observations (e.g., Robertson and Kravtsov 2008, Gnedin et al. 2009, Pelupessy and Papadopoulos 2009, Christensen et al. 2012). Fully-time-dependent chemodynamical simulations that do not rely on such methods are restricted to either simple low-dimensional geometries (Koyama and Inutsuka 2000, Bergin et al. 2004) or to regions smaller than typical GMCs (Glover and Mac Low 2007a, 2007b, Glover et al. 2010, Glover and Mac Low 2011, Clark et al. 2012, Inoue and Inutsuka 2012).

One active area of research is whether the H i to H₂ or C⁺ to CO transitions are either necessary or sufficient for star formation. For CO the answer appears to be "neither". The nearly fixed ratio of CO surface brightness to star formation rate we measure in Solar metallicity regions (see Section 2.1) drops dramatically in low metallicity ones (Gardan et al. 2007, Wyder et al. 2009, Bolatto et al. 2011, 2013), strongly suggesting that the loss of metals is changing the carbon chemistry but not the way stars form. Numerical simulations suggest that, at Solar metallicity, CO formation is so rapid that even a cloud undergoing free-fall collapse will be CO-emitting by the time there is substantial star formation (Hartmann et al. 2001, Heitsch and Hartmann 2008a). Conversely, CO can form in shocks even if the gas is not self-gravitating (Dobbs et al. 2008, Inoue and Inutsuka 2012). Moreover, formation of CO does not strongly affect the temperature of molecular clouds, so it does not contribute to the loss of thermal support and onset of collapse (Krumholz et al. 2011, Glover and Clark 2012a). Thus it appears that CO accompanies star formation, but is not causally related to it.

The situation for H₂ is much less clear. Unlike CO, the correlation between star formation-H₂ correlation appears to be metallicity-independent, and is always stronger than the star formation-total gas correlation. Reducing the metallicity of a galaxy at fixed gas surface density lower both the H₂ abundance and star formation rate, and by nearly the same factor (Wolfe and Chen 2006, Rafelski et al. 2011, Bolatto et al. 2011). This still does not prove causality, however. Krumholz et al. (2011) and Glover and Clark (2012a) suggest that the explanation is that both H₂ formation and star formation are triggered by shielding effects. Only at large extinction is the photodissociation rate suppressed enough to allow H₂ to become dominant, but the same photons that dissociate H₂ also heat the gas via the grain photoelectric effect, and gas only gets cold enough to form stars where the photoelectric effect is suppressed. This is, however, only one possible explanation of the data.

A final question is whether the chemical conditions in GMCs are in equilibrium or non-equilibrium. The gas-phase ion-neutral reactions that lead to CO formation have high rates even at low temperatures, so carbon chemistry is likely to be in equilibrium (Glover et al. 2010, Glover and Mac Low 2011, Glover and Clark 2012b). The situation for H₂ is less clear. The rate coefficient for H₂ formation on dust grain surfaces is quite low, so whether gas can reach equilibrium depends on the density structure and the time available. Averaged over ~ 100 pc size scales and at metallicities above ~ 1% of Solar, Krumholz and Gnedin (2011) find that equilibrium models of Krumholz et al. (2009a) agree very well with time-dependent ones by Gnedin et al. (2009), and the observed metallicity-dependence of the H i-H₂ transition in external galaxies is also consistent with the predictions of the equilibrium models (Fumagalli et al. 2010, Bolatto et al. 2011, Wong et al. 2013). However, Mac Low and Glover (2012) find that equilibrium models do not reproduce their simulations on ~ 1-10 pc scales. Nonetheless, observations of Solar Neighborhood clouds on such scales appear to be consistent with equilbrium (Lee et al. 2012). All models agree, however, that non-equilibrium effects must become dominant at metallicities below ~ 1-10% of Solar, due to the reduction in the rate coefficient for H₂ formation that accompanies the loss of dust (Krumholz 2012, Glover and Clark 2012b).