4. STRUCTURE, EVOLUTION, AND DESTRUCTION

Now that we have sketched out how GMCs come into existence, we consider the processes that drive their internal structure, evolution, and eventual dispersal.

4.1. GMC Internal Structure

GMCs are characterized by a very clumpy, filamentary structure (see the reviews by André et al. and Molinari et al. in this volume), which can be produced by a wide range of processes, including gravitational collapse (e.g., Larson 1985, Nagai et al. 1998, Curry 2000, Burkert and Hartmann 2004), non-self-gravitating supersonic turbulence (Padoan et al. 2001), and colliding flows plus thermal instability (Audit and Hennebelle 2005, Vázquez-Semadeni et al. 2006); all these processes can be magnetized or unmagnetized. Some recent observational studies argue that the morphology is consistent with multi-scale infall (e.g., Galván-Madrid et al. 2009, Schneider et al. 2010, Kirk et al. 2013), but strong conclusions will require quantitative comparison with a wide range of simulations.

One promising approach to such comparisons is to develop statistical measures that can be applied to both simulations and observations, either two-dimensional column density maps or three-dimensional position-position-velocity cubes. Padoan et al. (2004b, a) provide one example. They compare column density PDFs produced in simulations of sub-Alfvénic and super-Alfvénic turbulence, and argue that observed PDFs are better fit by the super-Alfvénic model. This is in some tension with observations showing that magnetic fields remain well-ordered over a wide range of length scales (see the recent review by Crutcher (2012) and Li et al., this volume). The need for super-Alfvénic turbulence in the simulations may arise from the fact that they did not include self-gravity, thus requiring stronger turbulence to match the observed level of structure (Vázquez-Semadeni et al. 2008). Nevertheless, the Padoan:2004 results probably do show that magnetic fields cannot be strong enough to render GMCs sub-Alfvénic.

A second example comes from Brunt (2010), Brunt et al. (2010a, b) and Price et al. (2011), who use the statistics of the observed 2D column density PDF to infer the underlying 3D volume density PDF, and in turn use this to constrain the relationship between density variance and Mach number in nearby molecular clouds. They conclude from this analysis that a significant fraction of the energy injection that produces turbulence must be in compressive rather than solenoidal modes. Various authors (Kainulainen et al. 2009a, Kritsuk et al. 2011, Ballesteros-Paredes et al. 2011a, Federrath and Klessen 2013) also argue that the statistics of the density field are also highly sensitive to the amount of star formation that has taken place in a cloud, and can therefore be used as a measure of evolutionary state.

4.2. Origin of Nonthermal Motions

As discussed in Section 2.3, GMCs contain strong nonthermal motions, with the bulk of the energy in modes with size scales comparable to the cloud as a whole. For a typical GMC density of ~ 100 cm^-3, temperature of ~ 10 K, and bulk velocity of ~ 1 km s^-1, the viscous dissipation scale is ~ 10¹² cm (~ 0.1 AU), implying that the Reynolds number of these motions is ~ 10⁹. Such a high value of the Reynolds number essentially guarantees that the flow will be turbulent. Moreover, since the bulk velocity greatly exceeds the sound speed, the turbulence must be supersonic, though not necessarily super-Alfvénic. Zuckerman and Evans (1974) proposed that this turbulence would be confined to small scales, but modern simulations of supersonic turbulence indicate that the power is mostly on large scales. It is also possible that the linewidths contain a significant contribution from coherent infall, as we discuss below.

While turbulence is expected, the deeper question is why the linewidths are so large in the first place. Simulations conducted over the last ~ 15 years have generally demonstrated that, in the absence of external energy input, turbulence decays in ~ 1 crossing time of the outer scale of the turbulent flow (Mac Low et al. 1998, Mac Low 1999, Stone et al. 1998, Padoan and Nordlund 1999), except in the case of imbalanced MHD turbulence (Cho et al. 2002). Thus the large linewidths observed in GMCs would not in general be maintained for long periods in the absence of some external input. This problem has given rise to a number of proposed solutions, which can be broadly divided into three categories: global collapse, externally-driven turbulence, and internally-driven turbulence.

4.2.1 The Global Collapse Scenario

The global collapse scenario, first proposed by Goldreich and Kwan (1974) and Liszt et al. (1974), and more recently revived by Vázquez-Semadeni et al. (2007, 2009), Heitsch and Hartmann (2008a, b), Heitsch et al. (2009), Ballesteros-Paredes et al. ( 2011b, a), and Hartmann et al. (2012) as a nonlinear version of the hierarchical fragmentation scenario proposed by Hoyle (1953), offers perhaps the simplest solution: the linewidths are dominated by global gravitational collapse rather than random turbulence. This both provides a natural energy source (gravity) and removes the need to explain why the linewidths do not decay, because in this scenario GMCs, filaments, and clumps are not objects that need to be supported, but rather constitute a hierarchy of stages in a global, highly inhomogeneous collapse flow, with each stage accreting from its parent (Vázquez-Semadeni et al. 2009).

Investigations of this scenario generally begin by considering an idealized head-on collision between two single-phase, warm, diffuse gas streams, which might be caused by either local feedback or large-scale gravitational instability (cf. Section 3). (Simulations of more realistic glancing collisions between streams already containing dense clumps have yet to be performed.) The large scale compression triggers the formation of a cold cloud, which quickly acquires many Jeans masses because the warm-cold phase transition causes a factor of ~ 100 increase in density and a decrease by the same factor in temparature. Thus the Jeans mass, M_J ∝ ^-1/2 T^3/2, decreases by a factor ~ 10⁴ (e.g., Vazquez-Semadeni 2012). The cloud therefore readily fragments into clumps (Heitsch et al. 2005, Vázquez-Semadeni et al. 2006), and the ensemble of clumps becomes gravitationally unstable and begins an essentially pressure-free collapse. It contracts first along its shortest dimension (Lin et al. 1965), producing sheets and then filaments (Burkert and Hartmann 2004, Hartmann and Burkert 2007, Vázquez-Semadeni et al. 2007, 2010, 2011, Heitsch and Hartmann 2008a, Heitsch et al. 2009). Although initially the motions in the clouds are random and turbulent, they become ever-more infall-dominated as the collapse proceeds. However, because these motions have a gravitational origin, they naturally appear virialized (Vázquez-Semadeni et al. 2007, Ballesteros-Paredes et al. 2011b). Accretion flows consistent with the scenario have been reported in several observational studies of dense molecular gas (e.g., Galván-Madrid et al. 2009, Schneider et al. 2010, Kirk et al. 2013), but observations have yet to detect the predicted inflows at the early, large-scale stages of the hierarchy. These are difficult to detect because it is not easy to separate the atomic medium directly connected to molecular clouds from the general H i in the galaxy, and because the GMCs are highly fragmented, blurring the inverse p-Cygni profiles expected for infall. In fact, Heitsch et al. (2009) show that the CO line profiles of chaotically collapsing clouds match observations of GMCs.

While this idea elegantly resolves the problem of the large linewidths, it faces challenges with respect to the constraints imposed by the observed 20-30 Myr lifetimes of GMCs (Section 2.5) and the low rates and efficiencies of star formation (Section 2.6). We defer the question of star formation rates and efficiencies to Section 5. Concerning GMC lifetimes, a semi-analytic model by Zamora-Avilés et al. (2012) for the evolution of the cloud mass and SFR in this scenario shows agreement with the observations within factors of a few. Slightly smaller timescales (~ 10 Myr) are observed in numerical simulations of cloud build-up that consider the evolution of the molecular content of the cloud (Heitsch and Hartmann 2008a), although these authors considered substantially smaller cloud masses and more dense flows. Simulations considering larger cloud masses (several 10⁴ M) exhibit evolutionary timescales ~ 20 Myr (Colín et al. 2013), albeit no tracking of the molecular fraction was performed there. Simulations based on the global collapse scenario have not yet examined the formation and evolution of clouds of masses above 10⁵ M, comparable to those studied in extragalactic observations. Moreover, in all of these models the lifetime depends critically on the duration and properties of the gas inflow that forms the clouds, which is imposed as a boundary condition. Self-consistent simulations in which the required inflows are generated by galactic scale flows also remain to be performed.

4.2.2 The External Driving Scenario

The alternative possibility is that the large linewidths of GMCs are dominated by random motions rather than global collapse. This would naturally explain relatively long GMC lifetimes and (as we discuss in Section 5) low star formation rates, but in turn raises the problem of why these motions do not decay, giving rise to a global collapse. The external driving scenario proposes that this decay is offset by the injection of energy by flows external to the GMC. One obvious source of such external energy is the accretion flow from which the cloud itself forms, which can be subject to non-linear thin shell instability (Vishniac 1994) or oscillatory overstability (Chevalier and Imamura 1982) that will drive turbulence. Klessen and Hennebelle (2010) point out that only a small fraction of the gravitational potential energy of material accreting onto a GMC would need to be converted to bulk motion before it is dissipated in shocks in order to explain the observed linewidths of GMCs, and semi-analytic models by Goldbaum et al. (2011) confirm this conclusion. Numerical simulations confirm that cold dense layers confined by the ram pressure of accretion flows indeed are often turbulent (Hunter et al. 1986, Stevens et al. 1992, Walder and Folini 2000, Koyama and Inutsuka 2002, Audit and Hennebelle 2005, Heitsch et al. 2005, Vázquez-Semadeni et al. 2006), although numerical simulations consistently show that the velocity dispersions of these flows are significantly smaller than those observed in GMCs unless the flows are self-gravitating (Koyama and Inutsuka 2002, Heitsch et al. 2005, Vázquez-Semadeni et al. 2007, 2010). This can be understood because the condition of simultaneous thermal and ram pressure balance implies that the Mach numbers in both the warm and cold phases are comparable (Banerjee et al. 2009).

While accretion flows are one possible source of energy, there are also others. Galactic-scale and kpc-scale simulations by Tasker and Tan (2009), Tasker (2011), Dobbs et al. (2011a, b, 2012), Dobbs and Pringle (2013), Hopkins et al. (2012), Van Loo et al. (2013) all show that GMCs are embedded in large-scale galactic flows that subject them to continuous external buffeting - cloud-cloud collisions, encounters with shear near spiral arms, etc. - even when the cloud's mass is not necessarily growing. These external motions are particularly important for the most massive clouds, which preferentialy form via large-scale galactic flows, and can drive turbulence in them over a time significantly longer than _ff. This mechanism seems particularly likely to operate in high-surface density galaxies where the entire ISM is molecular and thus there is no real distinction between GMCs and other gas, and in fact seems to be required to explain the large velocity dispersions observed in high-redshift galaxies (Krumholz and Burkert 2010).

4.2.3 The Internal Driving Scenario

The internally-driven scenario proposes that stellar feedback internal to a molecular cloud is responsible for driving turbulence and explaining the large linewidths seen, in conjunction with externally-driven turbulence in the very rare clouds without significant star formation (e.g., the so-called Maddalena's cloud; Williams et al. 1994). There are a number of possible sources of turbulent driving, including H ii regions, radiation pressure, protostellar outflows, and the winds of main sequence stars. (Supernovae are unlikely to be important as an internal driver of turbulence in GMCs in most galaxies because the stellar evolution timescale is comparable to the crossing timescale, though they could be important as an external driver, for the dispersal of GMCs, and in starburst galaxies, see below). Matzner (2002) and Dekel and Krumholz (2013) provide useful summaries of the momentum budgets associated with each of these mechanisms, and they are discussed in much more detail in the chapter by Krumholz et al. in this volume.

H ii regions are one possible turbulent driver. Krumholz et al. (2006) and Goldbaum et al. (2011) conclude from their semi-analytic models that H ii regions provide a power source sufficient to offset the decay of turbulence, that most of this power is distributed into size scales comparable to the size of the cloud, and that feedback power is comparable to accretion power. The results from simulations are less clear. Gritschneder et al. 2009 and Walch et al. 2012 find that H ii regions in their simulations drive turbulence at velocity dispersions comparable to observed values, while Dale et al. (2005, 2012, 2013) and Colín et al. 2013 find that H ii regions rapidly disrupt GMCs with masses up to ~ 10⁵ M within less than 10 Myr (consistent with observations showing that > 10 Myr-old star clusters are usually gas-free - Leisawitz et al. 1989, Mayya et al. 2012), but do not drive turbulence. The origin of the difference is not clear, as the simulations differ in several ways, including the geometry they assume, the size scales they consider, and the way that they set up the initial conditions.

Nevertheless, in GMCs where the escape speed approaches the 10 km s^-1 sound speed in photoionized gas, H ii regions can no longer drive turbulence nor disrupt the clouds, and some authors have proposed that radiation pressure might take over (Thompson et al. 2005, Krumholz and Matzner 2009, Fall et al. 2010, Murray et al. 2010, Hopkins et al. 2011, 2012). Simulations on this point are far more limited, and the only ones published so far that actually include radiative transfer (as opposed to a sub-grid model for radiation pressure feedback) are those of Krumholz and Thompson (2012), Krumholz and Thompson (2013), who conclude that radiation pressure is unlikely to be important on the scales of GMCs. Figure 6 shows a result from one of these simulations.

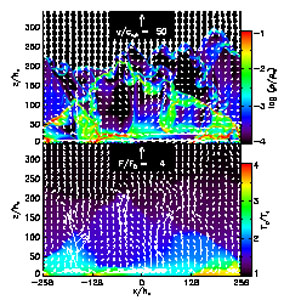Figure 6. Time slice from a radiation-hydrodyanmic simulation of a molecular cloud with a strong radiation flux passing through it. In the top panel, color shows density and arrows show velocity; in the bottom panel, color shows temperature and arrows show radiation flux. Density and temperature are both normalized to characteristic values at the cloud edge; velocity is normalized to the sound speed at the cloud edge, and flux to the injected radiation flux. The simulation demonstrates that radiation pressure-driven turbulence is possible, but also that the required radiation flux and matter column density are vastly in excess of the values found in real GMCs. Figure taken from Krumholz and Thompson (2012).

Stellar winds and outflows can also drive turbulence. Winds from hot main-sequence stars have been studied by Dale and Bonnell (2008) and Rogers and Pittard (2013), who find that they tend to ablate the clouds but not to drive significant turbulence. On the other hand, studies of protostellar outflows find that on small scales they can maintain a constant velocity dispersion while simultaneously keeping the star formation rate low (Cunningham et al. 2006, Li and Nakamura 2006, Matzner 2007, Nakamura and Li 2007, Wang et al. 2010). On the other hand, these studies also indicate that outflows cannot be the dominant driver of turbulence on ~ 10-100 pc scales in GMCs, both because they lack sufficient power, and because they tend to produce a turbulent power spectrum with a distinct bump at ~ 1 pc scales, in contrast to the pure powerlaw usually observed.

Whether any of these mechanisms can be the dominant source of the large linewidths seen in GMCs remains unsettled. One important caveat is that only a few of the simulations with feedback have included magnetic fields, and Wang et al. (2010) and Gendelev and Krumholz (2012) show (for protostellar outflows and H ii regions, respectively) that magnetic fields can dramatically increase the ability of internal mechanisms to drive turbulence, because they provide an effective means of transmitting momentum into otherwise difficult-to-reach portions of clouds. MHD simulations of feedback in GMCs are clearly needed.

4.3. Mass Loss and Disruption

As discussed in Section 2.5, GMCs are disrupted long before they can turn a significant fraction of their mass into stars. The question of what mechanism or mechanisms are responsible for this is closely tied to the question of the origin of GMC turbulence discussed in the previous section, as each proposed answer to that question imposes certain requirements on how GMCs must disrupt. In the global collapse scenario, disruption must occur in less than the mean-density free-fall time to avoid excessive star formation. Recent results suggest a somewhat slower collapse in flattened or filamentary objects (Toalá et al. 2012, Pon et al. 2012), but disruption must still be fast. In the externally-driven or internally-driven turbulence scenarios disruption can be slower, but must still occur before the bulk of the material can be converted to stars. Radiation pressure and protostellar outflows appear unlikely to be responsible, for the same reasons (discussed in the previous section) that they cannot drive GMC-scale turbulence. For main sequence winds, Dale and Bonnell (2008) and Rogers and Pittard (2013) find that they can expel mass from small, dense molecular clumps, but it is unclear if the same is true of the much larger masses and lower density scales that characterize GMCs.

The remaining stellar feedback mechanisms, photoionization and supernovae, are more promising. Analytic models have long predicted that photoionization should be the primary mechanism for ablating mass from GMCs (e.g., Field 1970, Whitworth 1979, Cox 1983, Williams and McKee 1997, Matzner 2002, Krumholz et al. 2006, Goldbaum et al. 2011), and numerical simulations by Dale et al. (2012, 2013) and Colín et al. (2013) confirm that photoionization is able to disrupt GMCs with masses of ~ 10⁵ M or less. More massive clouds, however, may have escape speeds too high for photoionization to disrupt them unless they suffer significant ablation first.

Supernovae are potentially effective in clouds of all masses, but are in need of further study. Of cataloged Galactic supernova remnants, 8% (and 25% of X-ray emitting remnants) are classified as "mixed morphology," believed to indicate interaction between the remnant and dense molecular gas (Rho and Petre 1998). This suggests that a non-negligible fraction of GMCs may interact with supernovae. Because GMCs are clumpy, this interaction will differ from the standard solutions in a uniform medium (e.g., Cioffi et al. 1988, Blondin et al. 1998), but theoretical studies of supernova remnants in molecular gas have thus far focused mainly on emission properties (e.g., Chevalier 1999, Chevalier and Fransson 2001, Tilley et al. 2006) rather than the dynamical consequences for GMC evolution. Although some preliminary work (Kovalenko and Korolev 2012) suggests that an outer shell will still form, with internal clumps accelerated outward when they are overrun by the expanding shock front (cf. Klein et al. 1994, Mac Low et al. 1994), complete simulations of supernova remant expansion within realistic GMC enviroments are lacking. Obtaining a quantitative assessment of the kinetic energy and momentum imparted to the dense gas will be crucial for understanding GMC destruction.