2. METHODS TO MEASURE QUASAR BH MASSES

2.1. Virial BH Masses: From Reverberation Mapping to Single-Epoch Methods

Reverberation mapping  The broad emission line regions in AGNs are powered by photoionizations from the central source (e.g., Peterson 1997), an assumption now widely accepted based on observations of correlated broad line and continuum variations. In fact, this photoionization assumption led to the first suggestions (e.g., Bahcall et al. 1972) of lagged broad line responses to continuum variations, where the lag reflects the light travel time from the ionizing source to the broad line region (BLR). In the 1970s there were already reported lag measurements between broad emission line and continuum variations in several local Seyfert nuclei (e.g., Lyutyj & Cherepashchuk 1974). Despite the low data quality that may impact the reliability of the detection, these studies were among the first attempts to directly measure BLR sizes. This idea was later developed in greater detail by Blandford & McKee (1982), who suggested that by mapping the response function of the broad emission line to continuum variations one can in principle reconstruct the structure and kinematics of the BLR, a technique they coined "reverberation mapping" (RM). Today RM has become a practical and powerful tool to study BLRs (see reviews by, e.g., Peterson 1993, Netzer & Peterson 1997, Horne et al. 2004), whose spatial extent (~ sub-pc) is too small to be resolved by current instrumentation. There are now several dozens of AGNs and quasars (most are at z < 0.3) with average lag measurements (e.g., Kaspi et al. 2000, Peterson et al. 2004, Bentz et al. 2009b), although only a handful of them have decent velocity-resolved delay maps (e.g., Denney et al. 2009a, Bentz et al. 2010, Grier et al. 2013) to utilize the full power of RM.

RM lag measurements provide an estimate of the typical size of the BLR. If we further assume that the BLR is virialized and the motion of the emitting clouds is dominated by the gravitational field of the central BH, then the mass of the BH is determined by (e.g., Ho 1999, Wandel et al. 1999):

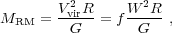(2)

where V_vir is the virial velocity and R is the BLR size. In practice we use the width of the broad line, W, as an indicator of the virial velocity, assuming that the broad line is Doppler broadened by the virial motion of the emitting gas. The product W² R / G is called the virial product. There are two commonly used line width definitions, the "full-width-at-half-maximum" (FWHM), and the line dispersion _line (i.e., the second moment of the line, Peterson et al. 2004). The pros and cons of both definitions will be discussed later. In computing the RM BH masses, both line widths are measured from the rms spectra from the monitoring period, thus only the variable part of the line contributes to the line width calculation.

To account for our ignorance of the structure and geometry of the BLR which determine the relation between the virial velocity and the line-of-sight (LOS) velocity inferred from W, we have introduced a virial coefficient (or geometrical factor), f ¹, in Eqn. (2). This is a big simplification, because the BLR structure and viewing angle determine the entire line profile, and the line width, being only one characteristic of the line profile, can not fully describe the underlying kinematic structure. Similarly it is an approximation to describe the BLR with a single radius R. Nevertheless, given the difficulties and ambiguities of modeling the line profile directly, Eqn. (2) involving line widths and f is used almost universally. For BLR clouds in randomly orientated orbits, an often quoted value is f 3/4 (3) if W = FWHM (_line) (Netzer 1990), although such a f value is derived under some simplifications and approximations and is not a rigorous analytic result. In practice, the value of f is now empirically determined by requiring that the derived RM masses are consistent with those predicted from the BH mass-bulge stellar velocity dispersion (M_BH - _*) relation of local inactive galaxies (e.g., Onken et al. 2004): f 1.4 (5.5) for W = FWHM (_line). This f value is of course then the averaged value for the subset of RM AGNs with bulge stellar velocity dispersion measurements. The uncertainty in f and the simplification of it as a single constant remain one of the major uncertainties in RM mass determinations, as further discussed in Section 3.1.2.

The uncertainty of the RM masses is typically a factor of a few, or ~ 0.4-0.5 dex (e.g., Peterson 2010), based on comparisons between RM masses and predictions from the M_BH - _* relation, and accounting for other potential systematics.

The R - L relation    Perhaps the most remarkable finding of RM observations is a tight correlation between the measured BLR size and the adjacent optical continuum luminosity L_opt (usually measured at restframe 5100 Å), R L, over ~ 4 orders of magnitude in luminosity. This is known as the BLR size-luminosity relation, or the R-L relation (e.g., Kaspi et al. 2000, Kaspi et al. 2005, Bentz et al. 2009a). To first order all broad line quasars have similar spectral energy distributions (SEDs) from X-ray to optical ², so L_opt is proportional to the ionizing continuum L_ion. The ionization parameter in a photoionized medium is U = Q(H) / (4 r² cn_e), where Q(H) L is the number of ionizing photons from the central source per second, c is the speed of light, and n_e is electron density. Thus a slope of = 0.5 in the R-L relation is expected, if U and the electron density are more or less constant in BLRs. Alternatively, a slope of = 0.5 is also predicted if the BLR size is set by dust sublimation (e.g., Netzer & Laor 1993).

Early RM work reported a slope of ~ 0.7 (e.g., Kaspi et al. 2000). Later work which carefully accounted for host starlight contamination to L_opt reported 0.5 (e.g., Bentz et al. 2009a), closer to naive expectations from photoionization. The intrinsic scatter of the R - L relation is estimated to be ~ 0.15 dex (~ 0.11 dex with the best quality RM data, Peterson 2010). The latest version of the R - L relation based on H RM measurements is (Bentz et al. 2009a):

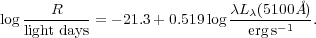(3)

The tightness of the R - L relation has led to suggestions to use this relation as an absolute luminosity indicator to use quasars as a cosmology probe (e.g., Watson et al. 2011, Czerny et al. 2012), although RM measurements of BLR sizes and quantification of the R - L relation beyond z ~ 0.3 are yet to come (e.g., Kaspi et al. 2007).

Single-epoch (SE) virial BH mass estimators  The observed R-L relation provides a much less expensive way to estimate the size of the BLR based on the luminosity of the quasar. Subsequently this relation has been used to develop the so-called "single-epoch virial black hole mass estimators" ³ (SE virial masses or SE masses in short hereafter): one estimates the BLR size from the measured quasar luminosity using the R - L relation, and the width of the broad emission line, which are then combined to give an estimate of the BH mass using calibration coefficients determined from the sample of AGNs with RM mass estimates. Specifically, these estimators take the form:

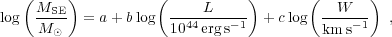(4)

where L and W are the quasar continuum (or line) luminosity and width for the specific line, and coefficients a, b and c are calibrated against RM AGNs. In Eqn. (4), the coefficient on line width is usually taken to be c = 2, as expected from viral motion. Other values of c are suggested, however, depending on the definition of line width, and will be discussed further in Section 3. Based on the general similarity of quasar SEDs (both continuum and line strength), different luminosities have been used, including continuum luminosities in X-ray, restframe UV and optical, as well as line luminosities, in various versions of these single-epoch virial estimators (e.g., Vestergaard 2002, McLure & Jarvis 2002, McLure & Dunlop 2004, Wu et al. 2004, Greene & Ho 2005, Vestergaard & Peterson 2006, Kollmeier et al. 2006, Onken & Kollmeier 2008, Wang et al. 2009, Vestergaard & Osmer 2009, Greene et al. 2010b, Rafiee & Hall 2011b, Shen et al. 2011, Shen & Liu 2012, Trakhtenbrot & Netzer 2012). In general continuum luminosities are preferred over line luminosities given their tighter correlations with BLR size, but in some cases line luminosities are preferred where the continuum may be significantly contaminated by host starlight (e.g., Greene & Ho 2005), or by the nonthermal emission from a jet in radio-loud objects (e.g., Wu et al. 2004). As for the choice of line width, both FWHM and line dispersion (_line) are utilized in these calibrations.

The uncertainty of these various single-epoch virial estimators can be inferred from the residuals in the calibrations against the RM masses, and is estimated to be on the order of ~ 0.5 dex (e.g., McLure & Jarvis 2002, Vestergaard & Peterson 2006). This is similar to the uncertainty of RM masses, and can hardly be smaller since this method is rooted in the RM technique. Reasons and consequences of such substantial mass uncertainties will be elaborated in Section 3. From now on I will refer to RM and SE masses collectively as virial BH masses.

The virial estimators (RM and SE) currently are the best method in estimating quasar BH masses. Therefore after a brief discussion on alternative methods (Section 2.2), I will focus on these virial estimators in the rest of the review.

2.2. Other Methods to Estimate Quasar BH Masses

There are several other methods to estimate the mass of quasars. They are much less popular than the RM method and its extension, the SE virial method. Nevertheless there is certain merit in further developing some of these methods, for instance, to provide complementary mass estimates and consistency checks. Therefore I give a brief discussion on these alternative methods.

Photoionization method  Historically Dibai was the first to systematically measure BH masses for quasar samples since the 1970s (e.g., Dibai 1977, Dibai 1980, Dibai 1984). Adopting Woltjer's postulation that the BLR gas is in virial equilibrium in the gravitational potential of the central BH (Woltjer 1959), Dibai used Eqn. (2) to estimate the BH mass, where the width of the line is used to indicate the virial velocity. To estimate the BLR size R, Dibai used the photoionization argument:

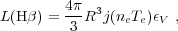(5)

where L(H) is the luminosity of the H line, j(n_e T_e) is the volume emissivity in the H line from photoionized gas, and є_V is the volume filling factor of BLR clouds. Adopting constant values of n_e 10⁹ cm^-3, T_e 10⁴ K and є_V 10^-3, Dibai estimated BH masses for more than ~ 70 nearby Seyfert 1 galaxies and quasars, and made the first plot of the distribution of AGNs in the mass-luminosity plane. Technically speaking, Dibai's method is also a single-epoch method, and it has an effective R - L relation of R L(H)^1/3, shallower than the observed R - L relation. Despite the simplifications in Dibai's approach (sometimes unphysical), many of his BH mass estimates of local AGNs are consistent with today's RM masses to within 0.3 dex (e.g., Bochkarev & Gaskell 2009). Dibai's method also motivated some later quasar BH mass estimations based on the same argument. For example, Wandel & Yahil (1985) used the same method with modifications to the volume filling factor, and derived a radius-luminosity relation R L(H)^1/2.

Along a completely independent path, photoionization arguments based on the ionization parameter U were used to estimate the BLR size (e.g., Netzer 1990, Wandel et al. 1999), building on earlier development of photoionization equilibrium theory in the 1970s (e.g., Davidson 1972, Davidson & Netzer 1979). This approach emphasizes more on the role of the ionization continuum, and provides an intuitive understanding of the observed R - L relation. But just as Dibai's method, all these photoionization-based methods require assumptions or indirect constraints on the physical conditions of the BLR gas (such as density, covering factor, etc) to infer the BLR size, therefore today they are not as popular as the more empirical, but more accurate RM-based methods discussed in Section 2.1.

Accretion disk model fitting (SED fitting)  Another method to infer the mass of the BH is by fitting the SED of quasars. The development of accretion disk theory over the last four decades (for a recent review, see, e.g., Abramowicz & Fragile 2013) has enabled predictions of the emitting continuum spectrum of accreting BHs. By fitting the observed quasar continuum SED, one can constrain the model parameters (such as BH mass, accretion rate, BH spin, inclination) with adequate accretion disk models. Many studies have used this SED fitting method to infer BH masses in AGNs (e.g., Malkan 1983, Sun & Malkan 1989, Wandel & Petrosian 1988, Laor 1990, Rokaki et al. 1992, Tripp et al. 1994, Ghisellini et al. 2010, Calderone et al. 2012), usually assuming a standard thin accretion disk model (Shakura & Sunyaev 1973). One main concern here is that standard accretion disk models, while can successfully produce broad-band features (such as the "big blue bump", e.g., Shields 1978), do not yet have the capability to fully explain the AGN SED (e.g., Koratkar & Blaes 1999, Lawrence 2012), and the resulting BH mass constraints may be sensitive to these deviations from standard accretion disk models. Given that there are parameter degeneracies and model assumptions/simplifications in the SED fitting procedure and the requirement for good multiwavelength coverage in UV-optical (where most of the disk emission comes from), this method generally cannot provide an accuracy of better than a factor of ~ five in BH mass estimates at the moment (e.g., Laor 1990, Calderone et al. 2012). But it would be interesting to compare this method with the virial methods (Section 2.1) for larger samples.

Microlensing in gravitationally lensed quasars – alternative routes to BLR sizes  Since resolving the BLRs requires µas to tens of µas angular resolution, RM will remain the primary method to measure the size of BLR in the next decade or two. Another indirect method to measure BLR size is via microlensing in gravitationally lensed quasars. The Einstein radius in the source (quasar) plane of a point-mass lens with mass M is r_e = √4GMD_s D_LS / (D_Lc²), where D_s, D_L and D_LS are the angular diameter distances to the source, to the lens, and from the lens to the sourse. For typical values z_L = 0.5 and z_s = 2 we have r_e 0.01√M / M pc, corresponding to an angular scale _e = r_e / D_s √M / M µas. This scale is comparable to the size of the BLR and accretion disk. Due to the relative transverse motion between the lens and source, large magnification can happen on short time scales (t_cross = r_source / v_⊥) during caustic-crossing in the source plane (for a primer on gravitational lensing, see, e.g., Schneider et al. 1992). Since the continuum emission (from the inner accretion disk) and BLR emission have different spatial scales ⁴ microlensing will cause differential variability for the continuum and different broad lines, which can be used to constrain the size (and geometry) of the emitting regions, such as the accretion disk and the BLR (e.g., Irwin et al. 1989, Lewis et al. 1998, Popovic et al. 2001, Richards et al. 2004a, Morgan et al. 2010, Dai et al. 2010, Mosquera & Kochanek 2011, Sluse et al. 2011, Sluse et al. 2012, Guerras et al. 2013). In particular, the latest study by Guerras et al. (2013) found a R - L relation based on microlensing BLR sizes, which is in reasonably good agreement with that based on RM. This technique is primarily applied to quasars that are already strongly lensed (with multiple images) for which the microlensing probability by stars/compact objects in the foreground lens galaxy is high, and the time delays between different images are known. The latter is important to rule out variability due to intrinsic AGN variability, which will often complicate the microlensing interpretation.

Direct dynamical BH masses  Although observationally challenging (given the overwhelming AGN continuum that dilutes the stellar absorption features and nongravitational forces on gas dynamics in the nucleus), there have been several attempts to get direct dynamical measurements of BH masses in Type 1 AGNs, using spatially resolved stellar kinematics (e.g., Davies et al. 2006, Onken et al. 2007) or gas kinematics (e.g., Hicks & Malkan 2008) down to the sphere of influence, R_SI = GM_BH / _*², of the BH. The number of AGNs with reliable dynamical BH mass measurements is still small, and it would be important to obtain more dynamical mass measurements of AGNs to provide critical consistency checks on virial BH masses.

Other indirect methods  These methods use correlations between BH mass and other measurable quantities, calibrated with known BH masses, to infer the BH mass in quasars. By virtue they can be applied to non-broad-line quasars as well, if the required quantity is measurable, but caution should be paid to possible systematics of each method. These correlations include the well-known BH-host scaling relations found for local inactive galaxies. For instance, the M_BH - _* relation in local inactive galaxies is used to predict BH masses in local RM AGNs with _* measurements (see Section 3.1.2). Another example is the observed anti-correlations between BH mass (estimated with other methods) and X-ray variability properties of AGNs, such as the break frequency in the power spectral densities (PSDs) of X-ray light curves or variability amplitude (e.g., Papadakis 2004, O'Neil et al. 2005, McHardy et al. 2006, Zhou et al. 2010), which have the potential to provide independent BH mass estimates to within a factor of a few to the RM masses. The reliability and systematics of the X-ray variability method, however, are yet to be explored with larger AGN samples with known BH masses.

¹ Some studies define the virial coefficient differently, i.e., V_vir ≡ fW (e.g., McLure & Jarvis 2002, Decarli et al. 2008a). Back.

² It is also important to recognize that AGN SEDs can vary significantly from object to object, and some of these variances in SED must introduce certain scatter in the observed R - L relation based on measurable continuum instead of the ionizing continuum, and may cause systematic changes of BLR structure with SED properties (which might affect the virial coefficient f). Back.

³ Such methods are also known as BH mass scaling methods (e.g., Vestergaard et al.2011). Occasionally, this method is referred to as the "photoionization method" (e.g., Peterson 2011, Salviander & Shields 2012). This may be a little ambiguous, since in practice this empirical method is based on RM results rather than photonionization calculations, even though the observed R - L relation is consistent with naive photoionization predictions. The "photoionization method" better refers to those that estimate the BLR size using photoionization arguments (see Section 2.2). Back.

⁴ The BLR and the accretion disk are probably not disjointed, i.e., some portion of the BLR gas could originate from the outer part of the accretion disk or from a wind launched from the disk, and high-ionization lines could have different origins from low-ionization lines, as in some models (e.g., Collin-Souffrin et al. 1988, Elvis 2000, Risaliti & Elvis 2010). Back.