


Building up magnetic fields in galaxies is a three-stage process: (1) seeding, (2) amplifying, (3) ordering and sustaining.
(1) Seed fields can be “primordial”, generated in the early Universe (Durrer & Neronov 2013), or they may originate from later epochs, e.g. during cosmological structure formation by the Weibel instability (Lazar et al. 2009), from plasma fluctuations in protogalaxies (Schlickeiser 2012; Schlickeiser & Felten (2013)), from injection by the first stars (Bisnovatyi-Kogan et al. 1973) or jets generated by the first black holes (Rees 2005) or from the Biermann mechanism in the first supernova remnants (Hanayama et al. 2005).
Indication for a weak all-pervasive intergalactic seed field as a relic from the early Universe comes from the non-detection of GeV γ–ray emission with the FERMI satellite from blazars, which were observed at TeV energies with the HESS observatory. The secondary particles generated by the TeV photons may be deflected by intergalactic fields of at least 10−16 G strength and a high volume filling factor (Dolag et al. 2011). However, fluctuations in the intergalactic plasma may also disperse the γ–ray emission (Broderick et al. 2012) (see also the discussion in Durrer & Neronov 2013). Analysis of the CMB power spectra data from PLANCK gave an upper limit of about 5 nG on a (comoving) scale of 1 Mpc (Planck Collaboration et al. 2015b).
(2) An efficient source of field amplification is turbulence in the gas driven by supernova explosions (Ferrière 1996) or by spiral shocks (Kim et al. 2006), called the small-scale dynamo. In protogalaxies this mechanism can amplify weak seed fields to several µG strength (the energy level of turbulence) within less than 108 yr (Kulsrud et al. 1997; Schleicher et al. 2010; Beck et al. 2012a; Rieder & Teyssier 2015). The resulting field is turbulent.
(3) The final and most time consuming stage is the ordering of the turbulent field. Numerical models of evolving galaxies show fast field amplification and ordering with help of differential rotation (Wang & Abel 2009; Kotarba et al. 2009), possibly supported by the magneto-rotational instability (MRI) (Gressel et al. 2013; Pakmor & Springel 2013). In these models the ordered magnetic field forms spiral arm segments, but it has frequent reversals in azimuthal and radial directions and hence is anisotropic turbulent (Sect. 3.1).
The most promising mechanism to sustain magnetic fields and generate large-scale regular fields from turbulent fields in the interstellar medium of galaxies is the α − Ω dynamo (Beck et al. 1996). It is based on differential rotation (Ω), expanding gas flows, driven by supernova explosions (Ferrière 1996; Gressel et al. 2013) or cosmic rays (Hanasz et al. 2009), carrying magnetic fields that are twisted by the Coriolis force (α–effect), and on magnetic diffusivity (η) driven by turbulence. The “mean-field” approximation of the α − Ω dynamo equation allows analytical solutions by mathematically separating the large-scale and small-scale parts of the velocity field and the magnetic field. The “mean-field” dynamo equation for the regular field B
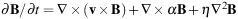 |
(1) |
describes the field amplification by the induction term ∇ × (v × B), where v is the large-scale velocity, the gain term ∇ × α B and the loss term η ∇2 B. MHD modeling with high spatial resolution showed that the scale separation of the mean-field approximation is reasonable (Gent et al. 2013).
Solutions of the mean-field dynamo equation are described by modes m with different azimuthal symmetries in the disk plane (axisymmetric, bisymmetric, quadri-symmetric, etc.) and two different vertical symmetries (even parity or odd parity) perpendicular to the disk plane. Several modes can be excited in the same object, where lower modes have shorter growth times and larger amplitudes. In flat, rotating objects like galaxy disks, the strongest mode is composed of a toroidal field of axisymmetric spiral shape within the disk (m = 0), without sign reversals across the equatorial plane, and a weaker poloidal field of even symmetry. Azimuthal dynamo modes can be identified observationally from the patterns of polarization angles and Faraday rotation measures of the diffuse polarized emission from galaxy disks (see Sect. 4.7).
Mean-field models of the α − Ω dynamo in galaxy disks predict that turbulent fields are transformed into large-scale regular fields within a few 109 yr (Beck et al. 1994; Arshakian et al. 2009; Rodrigues et al. 2015). Field reversals from the early phases may survive until today (Moss et al. 2012). Global numerical models of galaxies (Gissinger et al. 2009; Hanasz et al. 2009; Kulpa-Dybeł et al. 2011; Siejkowski et al. 2014) confirmed the basic results of the mean-field models.
The twisted field loops needed for the operation of the α − Ω dynamo generate large-scale helicity. 1 As total helicity in a system is a conserved quantity (Brandenburg & Subramanian 2005), small-scale fields with opposite helicity are generated which quench dynamo action, unless they are removed from the system (Shukurov et al. 2006). Hence, moderately fast outflows are essential for effective α − Ω dynamo action, but strong outflows can suppress dynamos. This leaves a certain range of outflow velocities for optimal dynamo action (Rodrigues et al. 2015). As outflows are strongest above spiral arms, the α − Ω dynamo is expected to be more efficient between the spiral arms (Chamandy et al. 2015).
The total magnetic field Btot can be presented as the quadratic sum of the regular field Breg generated by the α − Ω dynamo and the component Bturb generated by the small-scale dynamo. Tangling of Breg can produce another component, Btan. Btan and Bturb should be comparable, because both components are driven by the same turbulent gas motions. On the solar surface, the small-scale dynamo seems to be weak (Stenflo 2012), but may still operate in the solar interior. In contrast to the Sun, stars and planets, the regime of dynamo action is fully accessible in galaxies. The existence of the small-scale dynamo is of fundamental importance for the evolution of magnetic fields in galaxies. Without a small-scale dynamo the seed fields in protogalaxies would be much weaker and the generation of large-scale regular fields would take much longer. Turbulent and tangled fields can be distinguished with (future) high-resolution observations.
1 Magnetic helicity H is defined as H = A · (∇ × A), where A is the magnetic vector potential. Back.