


Strength is the fundamental quantity to estimate the dynamical importance of magnetic fields. The equipartition assumption (Sect. 3.4) is the only presently applicable method to measure the total field strength. Zeeman measurements will become possible in spiral galaxies with future radio telescopes, but will trace fields on small scales only.
The average equipartition strength (Eq. 4) of total fields (corrected for inclination) for a sample of 74 spiral galaxies is Btot = 9 ± 2 µG (Niklas 1995). The average strength of 21 bright galaxies observed between 2000 and 2010 is Btot = 17 ± 3 µG (Fletcher 2010). Gas-rich spiral galaxies with high star-formation rates, like M 51 (Fig. 5), M 83 (Fig. 7) and NGC 6946 (Fig. 13), have total field strengths of 20−30 µG in their spiral arms. The strongest total fields of 50−100 µG are found in starburst galaxies like M 82 (Adebahr et al. 2013), in the “Antennae” NGC 4038/9 (Chyży & Beck 2004), in nuclear starburst regions like in NGC 253 (Heesen et al. 2011a), and in barred galaxies (Beck et al. 2005). In such galaxies, energy losses of CREs can be strong, so that the equipartition values are underestimates (Sect. 3.4). Radio-faint galaxies like M 31 (Fig. 11) and M 33 have weaker total magnetic fields (about 6 µG). The similarity to the values derived for our Milky Way with various methods (Sect. 5) gives confidence that the equipartition assumption is valid.
Field strengths of 0.5−18 mG were detected in starburst galaxies by the Zeeman effect in the OH megamaser emission line at 18 cm wavelength (Robishaw et al. 2008). These values refer to highly compressed gas clouds and are not typical of the diffuse interstellar medium.
The strength of ordered fields in the sky plane as observed by polarized synchrotron emission varies strongly between galaxies, from 10–15 µG in M 51 and the magnetic arms of NGC 6946 (Fig. 13) to about 5 µG in the star-forming ring of M 31 (Fig. 11). The average strength of the ordered fields of 21 bright galaxies observed since 2000 is Bord,⊥ = 5 µG with a standard deviation of 3 µG and an average ratio Bord,⊥ / Btot of 0.3 (Fletcher 2010).
The only deep observation of an Sa galaxy, M 104, with a prominent dust ring, revealed ordered, partly regular magnetic fields (Krause et al. 2006). Spiral galaxies of type S0 and elliptical galaxies without an active nucleus have very little star formation and hence hardly produce CREs that could emit synchrotron emission. Irregular starburst galaxies show only spots of ordered fields (Heesen et al. 2011b). No ordered fields could be detected so far in dwarf irregular galaxies (Chyży et al. 2011).
4.2. Magnetic energy densities
The relative importance of various competing forces in the interstellar medium can be estimated by comparing the corresponding energy densities. The mean energy densities of the total (mostly turbulent) magnetic field and the total cosmic rays, averaged in rings of about 1 kpc width, are ≃ 10−11 erg cm−3 in NGC 6946 (Beck 2007), M 63, M 83, NGC 4736 (Basu & Roy 2013) and IC 342 (Fig. 3), and ≃ 10−12 erg cm−3 in M 33 (Tabatabaei et al. 2008). In all these galaxies the average magnetic energy density is similar to the average kinetic energy density of the turbulent motions of the neutral gas across the star-forming disk (assuming a constant turbulent velocity of 10 km s−1) and about 10 times larger than that of the warm ionized gas (but still 500–1000 times smaller than the energy density of the general rotation of the neutral gas). This result is similar to that derived for the Milky Way (Cox 2005). The ISM is a low–β plasma (where β is the ratio of thermal to magnetic energy densities). Magnetic fields are dynamically important.
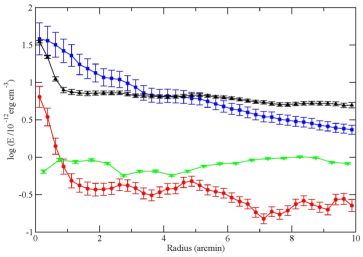 |
Figure 3. Radial variation of the energy densities in IC 342, determined from observations of synchrotron and thermal radio continuum and the CO and H I line emissions: for the total magnetic field Btot2/ 8π (black triangles), identical to that for the total cosmic rays, for the ordered magnetic field Bord2/8π (green triangles), for the turbulent motion of the neutral gas Eturb = 0.5 ρn vturb2 (blue squares), where vturb = 7 km/s, and for the thermal energy of the warm ionized gas Eth = 1.5 <ne> k Te (red circles), where Te = 104 K. The error bars include only errors due to rms noise in the images from which the energy densities are derived. No systematic errors are included, e.g. those imposed by a radial variation of thermal gas temperature, filling factor or turbulent gas velocity, nor errors due to deviations from the equipartition assumption (from (Beck 2015). |
According to Fig. 3, Eturb / Eth ≫ 1, i.e. turbulence is supersonic. Supersonic turbulence leads to shocks and hence dissipation of kinetic energy into heat, until turbulence becomes transonic and the system reaches an equilibrium state. The observation of supersonic turbulence may indicate that a quasi-steady state is never reached. However, observational bias effects need to be considered. The energy density of hot gas in the ISM, neglected in Fig. 3, is similar or somewhat larger than that of warm gas, depending on its volume filling factor (Ferrière 2001), so that its inclusion would not change the above result significantly. Another bias is the assumption of a constant gas temperature Te. If cosmic rays propagate via the streaming instability (Sect. 4.3), they may heat the gas and increase Te in the outer disk (Wiener et al. 2013).
Another important message from Fig. 3 (and similarly from the other galaxies studied so far) is that the magnetic energy density decreases radially more slowly than the kinetic energy density and dominates in the outer galaxy disk, i.e. the Alfvén velocity vA ∝ Btot / √ρ is larger than the turbulent velocity and increases with radius, which may cause magnetic effects on the rotation curve of the gas (Elstner et al. 2014). Note that the ratio of magnetic to kinetic energy may be even higher in the outer galaxy disk than shown in Fig. 3, because the equipartition field strengths are underestimates due to energy losses of the CREs (Sect. 3.4). Furthermore, the turbulent velocity tends to decrease with radius (Tamburro et al. 2009), which would also enhance the ratio of magnetic to kinetic energy.
Possible reasons why equipartition between magnetic and kinetic energy density does not hold within galaxies are:
(1) energy or pressure balance is valid between the magnetic field and the sum of pressures related to all gas components (kinetic and thermal) (Basu & Roy 2013);
(2) the efficiency of the small-scale dynamo increases from the inner to the outer galaxy;
(3) the magneto-rotational instability (MRI) leads to super-equipartition fields (Fig. 7 in Gressel et al. 2013);
(4) the equipartition field strengths are underestimated in the inner galaxy and overestimated in the outer galaxy due to CRE propagation (see Sect. 3.4), hence flattening the profile of the magnetic energy density.
Scenario (4) is supported by the analysis of radio and IR images (Berkhuijsen et al. 2013) and the cross-correlation based on wavelet transforms that breaks down below a certain scale that can be interpreted as the propagation length of CREs (Tabatabaei et al. 2013a). CRE propagation in IC 342 seems to be exceptionally fast (Sect. 4.3).
The energy density of the ordered magnetic field (Fig. 3) even increases radially. This field may be assumed to be mostly regular, so that we can invoke the α − Ω dynamo that also operates in the outer disk of galaxies (Mikhailov et al. 2014). Although the star-formation activity is low in the outer disk, the magneto-rotational instability (MRI) may serve as the source of turbulence required for α − Ω dynamo action (Sellwood & Balbus 1999; Gressel et al. 2013). Alternatively, regular fields generated in the inner disk could be transported outwards by the joint action of a dynamo and turbulent diffusivity (Moss et al. 1998).
The measurable extent Lsyn of synchrotron disks or halos (see Sect. 4.13) gives us information about the extent of the total magnetic field and the propagation of CREs. Under energy equipartition conditions, the radial exponential scale length of the total field in a disk of mildly inclined galaxies (or the vertical exponential scale height in a halo of almost edge-on galaxies) is LB ≥ (3+α) Lsyn, where α≃ 0.9 is the synchrotron spectral index. The scale length LCR (or scale height) of the total cosmic rays is half of this value. These are lower limits because the CREs lose their energy with distance from the star-forming disk, so that the equipartition assumption yields too small values for the field strength (Sect. 3.4). The scale lengths of synchrotron disks of typically Lsyn ≃3−5 kpc at 20 cm wavelength (Beck 2007; Basu & Roy 2013; Mulcahy et al. 2014) yield LB ≃ 12−19 kpc and LCR ≃ 6−9.5 kpc. The nearby galaxy IC 342 (Fig. 6) reveals an exceptionally large synchrotron scale length of about 16 kpc (Beck 2015).
The radial scale length and its frequency dependence give us a general idea about the speed and type of CRE propagation. At wavelengths of ≥1 m, synchrotron and inverse Compton losses are weaker than at shorter wavelengths, so that CREs can diffuse further outwards from their locations of origin. This is clearly seen in M 31 and M 33 (Berkhuijsen et al. 2013). The LOFAR image of the galaxy M 51 at 2 m wavelength reveals a steepening of the radial distribution of synchrotron emission, located at about 10 kpc radius, beyond the sharp decrease in the star-formation rate, indicating a propagation length of a few kpc (Mulcahy et al. 2014). The frequency dependence of the scale length favours diffusive propagation in the cases of M 51 and several other galaxies (Basu & Roy 2013; Berkhuijsen et al. 2013; Mulcahy et al. 2014) and fast convective transport in IC 342 (Beck 2015).
The galactic fields may extend further out into intergalactic space than visible in radio synchrotron images. A large radial scale length means that magnetic fields may affect the global rotation of the gas in the outer parts of spiral galaxies, possibly explaining some fraction of the flattening of the rotation curves (Battaner & Florido 2007; Elstner et al. 2014).
4.4. Relations between gas, star formation and magnetic fields
Radio continuum and infrared emissions from galaxies are closely correlated.
Firstly, a global correlation exists between the galaxy-integrated luminosity of the total radio continuum emission at around 20 cm wavelengths (frequencies of around 1 GHz), which is mostly of synchrotron origin, and the infrared (IR) luminosity of star-forming galaxies. This is one of the tightest correlations known in astronomy. The correlation extends over five orders of magnitude (Bell 2003), is slightly nonlinear in log-log scale (Bell 2003; Pierini et al. 2003) with an exponent of 1.09 ± 0.05 (Basu et al. 2015) and is valid in starburst galaxies to redshifts of at least four (Seymour et al. 2008), without evidence for evolution with redshift up to 1.2 (Basu et al. 2015). As the correlation between radio thermal and IR luminosity should be strictly linear, the exponent of the nonthermal (synchrotron)–IR correlation is steeper than 1.1. A breakdown of synchrotron emission and of its correlation with IR is expected beyond a critical redshift when inverse Compton loss of the CREs dominates synchrotron loss; this critical redshift will give us information about the field evolution in young galaxies (Schleicher & Beck 2013).
In galaxies with strong magnetic fields, e.g. in starburst galaxies, the CREs may lose their energy by synchrotron loss within the galaxy disk (“lepton calorimeter model”, Völk 1989), where the correlation is linear and due to the joint generation of CREs and dust-heating UV photons in star-forming regions, independent of the magnetic field. In Milky Way-type galaxies, magnetic fields are crucial to understand the correlation. Niklas & Beck (1997) proposed an “equipartition model”, where total (mostly turbulent) magnetic fields, cosmic rays, gas density and star formation are related, and predicted a nonlinear synchrotron–IR correlation with an exponent of about 1.3, in good agreement with observations. The more detailed analysis by Lacki et al. (2010) identified multiple feedback mechanisms that are not yet fully understood.
Secondly, the total radio and IR intensities within galaxies are also highly correlated, but with a smaller exponent, due to CRE propagation (Berkhuijsen et al. 2013). CRE propagation is also responsible for the flattening of the profile of cosmic-ray energy density in Fig. 3. The exponent of the correlation was found to be different in the central region, spiral arms and interarm regions in several nearby galaxies (Dumas et al. 2011; Basu et al. 2012), and it also differs between galaxies due to differences in the diffusion length of CREs (Berkhuijsen et al. 2013; Tabatabaei et al. 2013a).
The magnetic field and its structure play an important role in understanding the correlation (Tabatabaei et al. 2013a; Tabatabaei et al. 2013b). The synchrotron–IR correlation can be presented as a correlation between total field strength Btot and star-formation rate surface density ΣSFR with an exponent of 0.18 ± 0.01 within NGC 4254 (Chyży 2008), 0.14 ± 0.01 within NGC 6946 (Fig. 4), and 0.30 ± 0.02 (globally and locally) for a sample of 17 spiral galaxies (Heesen et al. 2014). A very similar exponent is expected from theoretical considerations (Schleicher & Beck 2013).
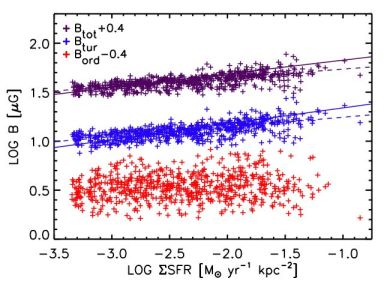 |
Figure 4. Correlation between the strength of the total, turbulent and ordered fields and the star-formation rate per area (determined from the 24 µm infrared intensities) within the galaxy NGC 6946. The points for Btot and Bord are shifted by +0.4 and -0.4, respectively, to fit into the same figure. The solid lines are bisector fits with slopes of 0.14 ± 0.01 for Btot and 0.16 ± 0.01 for Bturb, the dashed lines ordinary least-squares fits with slopes 0.089 ± 0.004 and 0.100 ± 0.005 (from Tabatabaei et al. 2013b and priv. comm.). |
The Kennicutt-Schmidt law ΣSFR ∝ Σgas N is valid within galaxies, with N≃1.0 for the molecular gas and N ≃1.5 for the atomic gas (Bigiel et al. 2008). 4 Then the above relation Btot ∝ ΣSFR0.30 corresponds to Btot ∝ Σgas0.30 if molecular gas dominates, e.g. in the inner regions of most spiral galaxies, and Btot ∝ Σgas0.45 in the outer regions that are dominated by atomic gas.
Turbulent fields in spiral arms are probably generated by turbulent gas motions related to star formation activity (Sect. 2). The small-scale dynamo predicts equipartition between magnetic and kinetic energy densities (Btot ∝ ρ0.5, assuming vturb = const), which is supported by the observed average values of a galaxy sample (Niklas & Beck 1997). However, within a galaxy the ratio between these energy densities decreases (Fig. 3), which is consistent with an exponent of <0.5 found from the ΣSFR data (see above). Possible reasons why equipartition between magnetic and kinetic energy density holds on average between galaxies, but not within galaxies, were discussed in Sect. 4.2.
The correlation between the radio continuum luminosity and the molecular gas (traced by its CO line emission) is similarly tight as the radio–IR correlation and is also nonlinear, with a slope of 1.31 ± 0.09 (Liu & Gao 2010). The correlation between the synchrotron radio continuum and CO intensities, observed with 60 pc resolution within the spiral galaxy M 51 (Schinnerer et al. 2013), appears to be tighter than the radio–IR correlation and may be the fundamental one. Much of the molecular gas in the spiral arms of M 51 is not directly associated with ongoing massive star formation, implying that star formation cannot be the sole cause for the radio–CO relation. Either the synchrotron emission emerges from secondary CREs that are produced in the interaction of cosmic-ray protons with the dense molecular material (Murgia et al. 2005), or the synchrotron emission is from primary CREs in strong magnetic fields coupled to the dense gas (Niklas & Beck 1997), in connection with fast diffusion of CREs along the spiral arms. High-resolution observations of nearby galaxies (e.g. with SKA and ALMA) can provide the necessary information on the coupling between magnetic fields and gas on small scales, to test which of the proposed origins for the correlation is indeed true.
In contrast to the turbulent field, the ordered field is either uncorrelated with the star-formation rate (Fig. 4) or anticorrelated in interarm regions, where the star-formation rate is low (Frick et al. 2001).
The most striking result from the observation of ordered (regular and/or anisotropic) fields with help of polarized synchrotron emission is that spiral patterns are found in almost every spiral galaxy (Beck & Wielebinski 2013), in galaxies with a star-forming ring (Chyży & Buta 2008), in flocculent galaxies without gaseous spiral arms (Soida et al. 2002), in central regions of galaxies (Fig. 17), and in circum-nuclear gas rings of barred galaxies (Fig. 16).
In galaxies with strong density waves like M 51 (Fig. 5) and M 83 (Fig. 7) enhanced ordered fields occur at the inner edges of the inner optical arms where the cold molecular gas is densest (Patrikeev et al. 2006). These are probably anisotropic turbulent fields generated by the compression of the density wave. An analysis of dispersions of the radio polarization angles at 6 cm wavelength in M 51 shows that the ratio of the correlation lengths parallel and perpendicular to the local ordered magnetic field is about two (Houde et al. 2013).
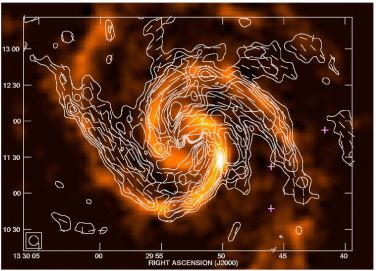 |
Figure 5. Polarized radio emission (contours) and B–vectors of M 51, combined from observations at 6 cm wavelength with the VLA and Effelsberg telescopes at 8′′ resolution (from Fletcher et al. 2011). The background colour image shows the CO line emission from molecular gas (from Helfer et al. 2003). |
In galaxies without strong density waves the ordered fields are not coinciding with the gaseous or the optical spiral arms. The typical degree of radio polarization at small wavelengths is only a few percent within the spiral arms, hence the field in the spiral arms must be mostly tangled or randomly oriented within the telescope beam on scales of a few 10 pc (Eq. 7).
Ordered fields are strongest (10−15 µG) in the regions between the spiral arms and oriented parallel to the adjacent spiral arms. In some galaxies they form magnetic arms, like in NGC 6946 (Fig. 13), with exceptionally high degrees of polarization up to 50%. These are probably generated by the α − Ω dynamo (Sect. 4.9).
The ordered magnetic field in the galaxy IC 342 reveals several spiral polarization arms of different origins (Fig. 6). In contrast to NGC 6946, there is only a rudimentary magnetic arm in an interarm region in the north-west, probably because of weaker dynamo action in IC 342 (Sect. 4.9). A narrow polarization arm of about 300 pc width, displaced inwards with respect to the inner arm east of the central region by about 200 pc, indicates that magnetic fields are compressed by a density wave, like in M 51. A broad polarization arm of 300–500 pc width around the northern optical arm shows systematic variations in polarized emission, polarization angles and Faraday rotation measures on a scale of about 2 kpc, indicative of a helically twisted flux tube generated by the Parker instability (Sect. 4.10). Several broad polarization arms in the outer galaxy are coincident with spiral arms in the total neutral gas.
 |
Figure 6. Polarization B–vectors of IC 342, combined from observations at 6 cm wavelength with the VLA and Effelsberg telescopes and smoothed to 25′′ resolution (from Beck 2015), overlaid on a colour image from the Kitt Peak Observatory (credit: T.A. Rector, University of Alaska Anchorage, and H. Schweiker, WIYN and NOAO/AURA/NSF). A region of 16′ × 16′ (about 16 × 16 kpc) is shown. (Copyright: MPIfR Bonn) |
At wavelengths of around 20 cm, most of the polarized emission from the far side of the disk and halo is Faraday-depolarized and the emission from the front side dominates. A striking asymmetry of the polarized emission occurs along the major axis of 12 spiral galaxies with inclinations of less than about 60∘. The emission is always much weaker around the kinematically receding side (positive radial velocities) of the major axis (Urbanik et al. 1997; Braun et al. 2010; Vollmer et al. 2013). This asymmetry is still visible at 11 cm wavelength, but disappears at smaller wavelengths where the polarized emission from the far side becomes observable. In strongly inclined galaxies, both sides of the major axis become Faraday-depolarized at around 20 cm. Modeling of a combination of disk and halo fields, as predicted by α − Ω dynamo models (Sect. 2), can explain the asymmetry (Braun et al. 2010).
At even longer wavelengths, Faraday effects depolarize the synchrotron emission almost completely. With help of Faraday Synthesis applied to 90 cm data from the Westerbork Synthesis Radio Telescope, an extremely low average degree of polarization of 0.21 ± 0.05% was measured in the star-forming “ring” of M 31 (Gießübel et al. 2013). No polarized emission could be detected from M 51 with the Low Frequency Array (LOFAR) at around 2 m wavelength – total Faraday depolarization occurs at such long wavelengths (Mulcahy et al. 2014).
In mean-field dynamo theory, the average pitch angle of the spiral magnetic field pB and the average pitch angle of the gaseous spiral arms pa are not related, while they are observed to be roughly similar in a limited sample of galaxies (Fig. 9). Within galaxies, too, the magnetic pitch angles are similar to the pitch angles of the gaseous spiral arm structures and of those of the polarized intensity, tracing the structures of the ordered field (e.g. Fig. 6). In IC 342 the magnetic pitch angle |pB| decreases with radius (Fig. 10), following the pitch angle of the gaseous spiral structures (Beck 2015).
The formation of spiral arms and spiral magnetic patterns seems to be related, as expected e.g. for MHD density waves (Lou et al. 1999). Almost identical pitch angles would indicate field alignment with the gas structures by shear or compression in density waves. However, based on anisotropic wavelet transformations, a systematic shift was detected in the barred galaxy M 83 (Fig. 7), in the sense that |pB| is larger than |pa| by about 20∘ (Fig. 8). Similar results were found in other galaxies. Such differences can be regarded as a signature of α − Ω dynamo action (Sect. 4.8).
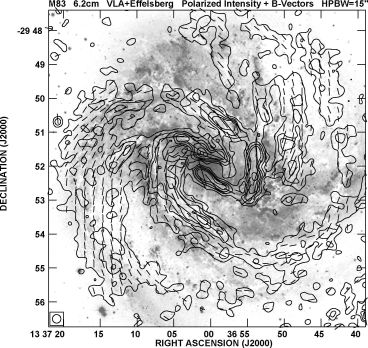 |
Figure 7. Polarized radio emission (contours) and B–vectors of M 83, combined from observations at 6 cm wavelength with the VLA and Effelsberg telescopes and smoothed to 15′′ resolution (from Frick et al. 2015), overlaid onto an optical image from Dave Malin, Anglo Australian Observatory. (Copyright: MPIfR Bonn and AAO) |
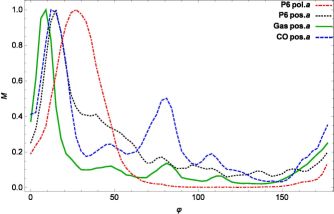 |
Figure 8. The power spectra of pitch angles of structures at the wavelet-filtered scale 1′ (about 2.6 kpc) in M 83, normalized to unit maximum: the pitch angles of the structures of polarized intensity at 6 cm wavelength (black dotted), total neutral gas (green) and molecular gas CO (blue dashed). The spectrum of the magnetic pitch angles is shown with the red dot-dashed curve (from Frick et al. 2015). |
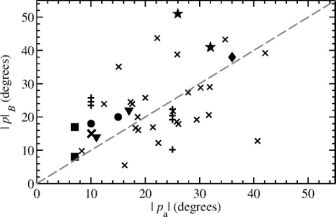 |
Figure 9. Average magnetic pitch angles |pB| and average pitch angles of gaseous spiral structures |pa| in several radial regions of 12 galaxies. The dashed line corresponds to |pB| = |pa| (from Van Eck et al. 2015). |
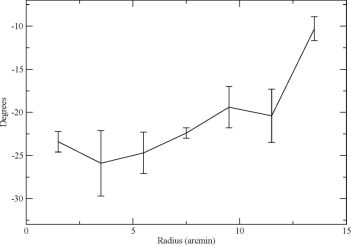 |
Figure 10. Azimuthally averaged magnetic pitch angle pB as a function of radius (in arcminutes) in the plane of IC 342. pB is negative in this galaxy, because the spiral pattern (see Fig. 6) turns outward in the clockwise sense (from Beck 2015). |
In the thin-disk approximation of the α − Ω dynamo, the magnetic pitch angle is given by |pB| = (Rα / RΩ)1/2, where Rα and RΩ are the dynamo numbers (Shukurov 2005). Simplified estimates for the dynamo numbers and a flat rotation curve, which is valid beyond a radius of about a few kpc in most spiral galaxies, give |pB| = d / H, where d is the turbulence scale (about 50 pc, see Fletcher et al. 2011), and H is the scale height of the ionized gas. The scale heights of H I disks in spiral galaxies increase radially (Bagetakos et al. 2011). One may speculate that the disk of ionized gas also flares (e.g. assumed in the model by Gressel et al. (2013)), which would explain the decrease of |pB| observed in many galaxies. If so, the radial variation of |pB| in IC 342 (Fig. 10) indicates that the scale height H is approximately constant until 12′ (about 12 kpc) radius and then increases. Alternatively, the magnetic pitch angle may be affected by gas flows, for instance by outflows that become weaker towards the outer disk and can decrease the effective dynamo number (Shukurov et al. 2006).
Spiral fields can be generated by compression in spiral arms, by shear in interarm regions or by dynamo action (Sect. 2). Measuring Faraday rotation (Sect. 3.6) is crucial to distinguish between these mechanisms. Large-scale sinusoidal patterns of Faraday rotation measures (RM) along azimuthal angle in the galaxy plane (modes) are signatures of regular fields generated by the α − Ω dynamo and can be identified in RM derived from polarized emission from the galaxy disks at several frequencies (Krause 1990) or in RM data of polarized background sources (Stepanov et al. 2008). If several modes are superimposed, a Fourier analysis of the RM variation with azimuthal angle is needed. The resolution and sensitivity of present-day radio observations is sufficient to identify 2–3 modes.
The disks of about a dozen nearby spiral galaxies reveal large-scale RM patterns. The Andromeda galaxy M 31 (Fig. 11) is the prototype of a dynamo-generated axisymmetric spiral disk field, with a striking sinusoidal RM variation along the star-forming ring (Fig. 12), which is a strong indication of an axisymmetric spiral field (mode m = 0) (Fletcher et al. 2004). Other candidates for a dominating axisymmetric disk field are the nearby spirals IC 342 (Sokoloff et al. 1992; Beck 2015) and NGC 253 (Heesen et al. 2009b). The axisymmetric field in the irregular Large Magellanic Cloud (LMC) is almost azimuthal (i.e. small pitch angles) (Gaensler et al. 2005; Mao et al. 2012). Dominating bisymmetric spiral fields (mode m = 1) are rare, as predicted by dynamo models, but possibly exist in M 81 (Krause et al. 1989; Sokoloff et al. 1992). Faraday rotation in NGC 6946 and in other similar galaxies with magnetic arms can be described by a superposition of two azimuthal modes (m = 0 and m = 2) with about equal amplitudes, where the quadrisymmetric (m = 2) mode is phase shifted with respect to the density wave (Beck 2007). For several other galaxies, three modes (m = 0, 1 and 2) are necessary to describe the data (Table 2).
| Galaxy | m = 0 | m = 1 | m = 2 | Reference |
| M 31 | 1 | 0 | 0 | Fletcher et al. (2004) |
| M 33 | 1 | 1 | 0.5 | Tabatabaei et al. (2008) |
| M 51 (disk) | 1 | 0 | 0.5 | Fletcher et al. (2011) |
| M 51 (halo) | 0 | 1 | 0 | Fletcher et al. (2011) |
| M 81 | 0.5 | 1 | – | Sokoloff et al. (1992) |
| NGC 253 | 1 | – | – | Heesen et al. (2009b) |
| NGC 1097 | 1 | 1 | 1 | Beck et al. (2005) |
| NGC 1365 | 1 | 1 | 1 | Beck et al. (2005) |
| NGC 4254 | 1 | 0.5 | – | Chyży (2008) |
| NGC 4414 | 1 | 0.5 | 0.5 | Soida et al. (2002) |
| NGC 6946 | 1? | – | 1? | Ehle & Beck (1993); Rohde et al. (1999) |
| IC 342 | 1 | – | – | Sokoloff et al. (1992); Beck (2015) |
| LMC | 1 | – | – | Gaensler et al. (2005); Mao et al. (2012) |
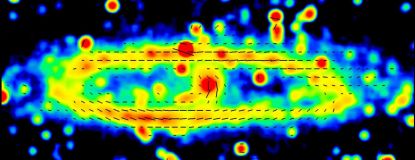 |
Figure 11. Total radio emission (colour) and B–vectors (corrected for Faraday rotation in the foreground of the Milky Way) in the Andromeda galaxy (M 31), observed at 6 cm wavelength with the Effelsberg telescope at 3′ resolution (from Gießübel 2012). (Copyright: MPIfR Bonn) |
 |
Figure 12. Faraday rotation measures between 6 cm and 11 cm wavelengths (colour, from blue = -175 rad m−2 to red = +25 rad m−2), total radio emission at 6 cm (contours) and B–vectors (corrected for Faraday rotation) in the Andromeda galaxy (M 31), observed with the Effelsberg telescope at 5′ resolution (from Berkhuijsen et al. 2003). (Copyright: MPIfR Bonn) |
The spiral pattern of magnetic fields cannot be solely the result of α − Ω dynamo action. If the beautiful spiral pattern of M 51 seen in radio polarization (Fig. 5) were only due to a regular field in the disk, its line-of sight component should generate a conspicuous large-scale pattern in RM, but this is not observed (Fletcher et al. 2011). This means that a large amount of the ordered field is anisotropic turbulent and probably generated by compression and shear of the non-axisymmetric gas flows in the density-wave potential. The anisotropic turbulent field is strongest at the positions of the prominent dust lanes on the inner edge of the inner gas spiral arms, due to compression of turbulent fields in the density-wave shock. A regular field (composed of modes m = 0 and m = 2) also exists in the disk of M 51, but is much weaker than the anisotropic turbulent field (Fletcher et al. 2011). Notably, RMs between 18 cm and 22 cm wavelengths, tracing only the polarized emission from regions nearest to the observer, show a large-scale pattern that indicates a regular field in the halo of M 51 (Heald et al. 2009; Fletcher et al. 2011; Mao et al. 2015).
The large-scale regular field in the nearby galaxy IC 342 is similarly weak as in M 51. It is only visible in the pattern of RMs obtained from the low-resolution Effelsberg images (Beck 2015), while RMs derived from the higher-resolution VLA images (Fig. 14) are about 10 times larger. The field direction changes along the northern spiral arm (Sect. 4.10).
The central regions of M 31 (Fig. 11) and IC 342 (Fig. 17) host regular spiral fields that are disconnected from the disk fields (Gießübel & Beck 2014; Beck 2015). As the direction of the radial field component points outwards, opposite to that of the disk field, two separate dynamos seem to operate in these galaxies.
In the disks of many other galaxies no clear pattern of Faraday rotation was found. Either several high-order modes are superimposed and cannot be distinguished with the limited sensitivity and resolution of present-day telescopes, or the timescale for the generation of large-scale modes is longer than the galaxy's lifetime (Arshakian et al. 2009). Also field injection by strong star-formation activity may perturb the generation of a large-scale regular field (Moss et al. 2012).
While the azimuthal symmetries of regular magnetic fields have been well observed in many galaxies (Table 2), the vertical symmetry (even or odd) is much harder to determine. The field of odd-symmetry modes reverses its sign above and below the galactic plane. The symmetry type is best visible in strongly inclined galaxies, via the RM signs above and below the galaxy plane. In mildly inclined galaxies the RMs of diffuse polarized emission from even and odd-symmetry fields differ by a factor of about two, which is hard to measure, while the RMs of background sources are close to zero for even symmetry (because the RM contributions from the two halves cancel) but large for odd symmetry. Background RMs in the area of the Large Magellanic Cloud (LMC) indicate an even-symmetry field (Mao et al. 2012). Indications for even-symmetry patterns were found in NGC 891 (Krause 2009) and NGC 5775 (Soida et al. 2011).
Spectro–polarimetric data of spiral galaxies are still rare and the application of Faraday Synthesis (Sect. 3.6) has just started (e.g. Gießübel et al. 2013; Mao et al. 2015). The Faraday spectrum reflects the distribution of regular magnetic fields, thermal gas and CREs and in principle allows tomography of the ISM in the disk and the halo. However, Faraday spectra do not have a simple correspondence to physical properties and cannot provide a straight-forward interpretation, as demonstrated by the models of Ideguchi et al. (2014).
Observations provide several qualitative evidences for the action of dynamos in spiral galaxies:
(1) The tight radio–IR correlation (Sect. 4.4) and the similarity of kinetic and magnetic energy densities (Fig. 3) indicate field amplification by turbulent gas motions generated by star-forming processes (Tabatabaei et al. 2013b; Schleicher & Beck 2013).
(2) The magnetic spiral patterns observed in all spiral galaxies so far indicate a general decoupling between magnetic fields and the (almost circular) gas flow due to magnetic diffusivity. The magnetic pitch angle deviates systematically from that of the spiral structures (e.g. in M 83, Fig. 8), as predicted by the α − Ω dynamo. Magnetic spiral patterns also exist in flocculent galaxies (Sect. 4.14). At present, no other model can explain the magnetic spiral patterns in the various types of galaxies.
(3) Large-scale regular fields are observed in all spiral galaxies so far (Table 2), an important result giving a strong hint to the action of α − Ω dynamos. No alternative model exists so far.
(4) By comparing the signs of the RM distribution and the velocity field on both sides of a galaxy's major axis, the inward and outward directions of the radial component of the axisymmetric spiral field can be distinguished (Krause & Beck 1998). Dynamo models predict that both signs should have the same probability, which is confirmed by observations. The axisymmetric fields of M 31, IC 342, NGC 253, and the axisymmetric field component in NGC 6946 point inwards, while those of NGC 891, NGC 4254 and NGC 5775 (Krause 2009), and the axisymmetric component of the disk field in M 51 (Fletcher et al. 2011) point outwards.
A major effort of quantitative comparisons between observable quantities and predictions was performed by Van Eck et al. (2015). Identifying the precise form of the connection between magnetic and other galactic properties is not straightforward because the parameters can combine to produce non-trivial scalings. For example, different physical mechanisms have been proposed to provide saturation of the field growth in dynamo models, like the balance between magnetic and kinetic (turbulent) forces, the balance between Coriolis and Lorentz forces, or outflows of hot gas carrying small-scale magnetic fields out of the disk in order to preserve the balance of magnetic helicity. These non-linear saturation mechanisms depend differently on galactic parameters, such as star-formation rate, gas density, rotational velocity, and rotational shear.
From their sample of 20 well-observed galaxies, Van Eck et al. (2015) found a statistically significant relation of the total magnetic field strength with the surface density of molecular gas and surface density of the star-formation rate, confirming earlier results (Sect. 4.4). The only other significant relation was found between the magnetic pitch angle and the strength of the axisymmetric spiral (m = 0) component of the regular field: a more tightly wound field has a stronger ASS component. However, IC 342 does not fit into this relation; has a tightly wound spiral field (Fig. 10), but only a weak axisymmetric component (Beck 2015).
In conclusion, dynamos certainly operate in all spiral galaxies, but other processes are amplifying and shaping the field as well. MHD density waves are compressing and aligning the field along the gaseous spiral arms. Non-axisymmetric gas flows around spiral arms and bars are shearing field lines. Parker instabilities form helically twisted field loops that are winding around spiral arms. To measure the importance of these competing or cooperating effects, the fundamental scaling relations between the properties of magnetic fields and the other galactic parameters need to be determined, based on radio observations of a large number of galaxies with high angular resolution.
Surprisingly, in most spiral galaxies observed so far the highest polarized intensities (i.e. the strongest ordered fields) are detected between the optical arms, filling a large fraction of the interarm space, sometimes concentrated in magnetic arms, as in NGC 6946 (Fig. 13). The southern-sky spiral galaxy NGC 2997 hosts compressed magnetic fields at the inner edges of material arms, as well as one well-developed magnetic arm (Han et al. 1999). The strong density waves in NGC 2997 lead to high degrees of polarization at 6 cm wavelength of typically 25% at the inner edge of the northern arm, similar to those in M 51 (Fletcher et al. 2011). The degree of polarization of the magnetic arm of 40% and its length of at least 10 kpc are similar to the values in NGC 6946 and are much higher than in IC 342 (Beck 2015). Like IC 342, M 51 has a short, rudimentary magnetic arm with a low degree of polarization (Fletcher et al. 2011). NGC 1566 shows signatures of a magnetic arm in the south-east (Ehle et al. 1996), but the angular resolution of these radio observations was too coarse to clearly detect magnetic arms. In large barred galaxies, ordered magnetic fields also fill most of the interarm space, e.g. in NGC 2442 (Harnett et al. 2004), NGC 1097, and NGC 1365 (Beck et al. 2005), but do not form well-defined magnetic arms.
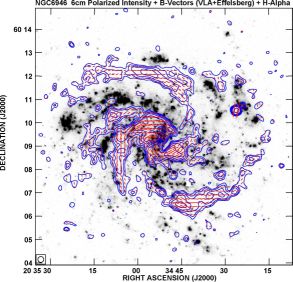 |
Figure 13. Polarized radio emission (contours) and B–vectors of NCC 6946, combined from observations at 6 cm wavelength with the VLA and Effelsberg telescopes and smoothed to 15′′ resolution (from Beck 2007), overlaid onto an Hα image from Anne Ferguson. (Copyright: MPIfR Bonn) |
Several mechanisms have been proposed to explain the high degree of field order in interarm regions:
(1) Magnetic field ropes as a result of a magnetic buoyancy instability in a turbulent high–β plasma (Kleeorin & Rogachevskii 1990); however, the ISM of galaxies is a low–β plasma, meaning that the thermal pressure is lower than the magnetic pressure (Sect. 4.2);
(2) slow MHD density waves in the rigidly rotating inner region of a galaxy (Lou et al. 1999; Poedts & Rogava 2002); however, slow MHD density waves in 3D can be subject to the Parker and shearing instabilities (Foglizzo & Tagger 1995);
(3) more efficient action of the mean-field dynamo between the optical arms due to lower turbulent velocity in interarm regions (Moss 1998; Shukurov 1998); however, the observed turbulent velocity is not lower in the interarm regions (e.g. in IC 342, Crosthwaite et al. 2001);
(4) introduction of a relaxation time of the magnetic response in the dynamo equation, leading to a phase shift between the material and magnetic spiral arms (Chamandy et al. 2013a; Chamandy et al. 2013b); however, the resulting magnetic arms are restricted to a relatively small region around the corotation radius and have a much smaller pitch angle than the gaseous arms;
(5) drift of magnetic fields with respect to the gaseous arms in a non-axisymmetric gas flow caused by a spiral perturbation (Otmianowska-Mazur et al. 2002) or by a bar (Kulpa-Dybeł et al. 2011);
(6) weakening of the mean-field dynamo in the material arms by continuous injection and amplification of turbulent fields by supernova shock fronts (Moss et al. 2013; Moss et al. 2015);
(7) weakening of the mean-field dynamo in the material arms by star-formation-driven outflows (Chamandy et al. 2015);
(8) magnetic arms as a transient phenomenon during the evolution of galactic magnetic fields, possibly related to the short lifetimes of spiral patterns seen in numerical simulations (e.g. (Dobbs & Baba 2014).
Models (5) – (8) are promising. Still, these models are simplified and consider either gravitational perturbations or dynamo action. Self-consistent MHD models of galaxies including the gravitational potential with spiral perturbations and mean-field dynamo action are still missing.
The origin of the rudimentary magnetic arm in IC 342 (Fig. 6) deserves a detailed discussion. The absence of long magnetic arms in IC 342 is surprising in view of the apparent similarities between IC 342 and NGC 6946, like the rotation curve and the star-formation surface density ΣSFR (Calzetti et al. 2010). The evolution of a spiral magnetic pattern in IC 342 may be hampered by the possible tidal interaction with the Local Group (Buta & McCall 1999) and/or by the complex spiral pattern in the gas of IC 342, described by a superposition of a two- and four-armed spiral pattern with different pattern speeds (Meidt et al. 2009), which may lead to an unstable spiral pattern. The mean-field dynamo needs a least a few rotation periods to build up a regular field (e.g. Moss et al. 2012). A short lifetime of a stable pattern may not allow the formation of magnetic arms.
The spiral pattern in the gas of M 51 is also distorted and short-lived, so that only a weak large-scale regular field and a rudimentary magnetic arm could develop. On the other hand, NGC 6946 has a two-armed spiral pattern with a well-defined pattern speed (Fathi et al. 2007), the spiral field extends smoothly into the central region (Beck 2007) and the large-scale regular field is strong (Ehle & Beck 1993). In summary, the existence of magnetic arms may indicate a stable spiral arm pattern over several galactic rotation periods, which may not be given in IC 342.
Most models of spiral gravitational perturbations in stars and gas have neglected the effect of magnetic fields so far. On the other hand, the only dynamo model for the amplification and ordering of magnetic fields including the spiral perturbations of gas density and gas velocity is the kinematical model by Otmianowska-Mazur et al. (2002), in which the back reaction of the field onto the gas flow was not included. The MHD model of Pakmor & Springel (2013) includes self-gravity and spiral perturbations, but no mean-field dynamo action. There is urgent need for a synergy between these approaches to achieve a comprehensive description of the evolving magnetized ISM in galaxies
4.10. Helically twisted Parker loops
IC 342 is one of the best studied nearby spiral galaxies. Its small distance and bright radio disk allows detailed studies of the magnetic field that are still impossible in most other galaxies.
Faraday rotation measures (Fig. 14) are found to vary periodically along the most prominent northern radio spiral arm. The average distance between the extrema corresponds to about 2.1 kpc. This feature can be interpreted as a magnetic loop (Parker instability) extending out of the galaxy's disk and out of the sky plane, giving rise to a periodic pattern in RM. A regular field bending out of the plane should lead to minima in polarized intensity (tracing the field component in the sky plane) at locations where |RM| (tracing the field component along the line of sight) is at its maximum. Minima of polarized intensity occur roughly at the locations of the extrema in RM, with a similar distance between the maxima or minima of about 2.2 kpc.
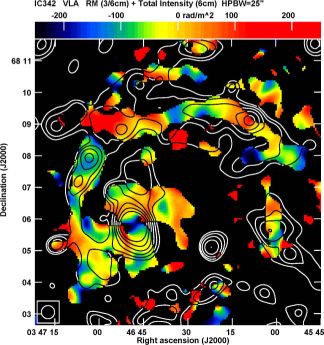 |
Figure 14. Faraday rotation measures (RM) between 3.5 cm and 6 cm wavelengths (colour) and total emission at 6 cm (contours) in the central and northern regions of IC 342, observed with the VLA at 25′′ resolution. RM is shown only at points where the polarized intensities at both wavelengths exceeds 3 times the rms noise (from Beck 2015). |
This is the second indication of a Parker loop in the magnetic field of a nearby galaxy, after M 31 (Beck et al. 1989). The numerical models by Kim et al. (2002) (who assume β = 1) predict a wavelength of the most unstable symmetric mode between 4 π H and 17 H, where H is the scale height of the gas. The peak-to-peak wavelength of about 4 kpc measured in IC 342 corresponds to H ≈ 230−320 pc, which is larger than typical scale heights of H I gas disks of spiral galaxies (Bagetakos et al. 2011). The reason for this discrepancy may be that the assumption of β = 1 is incorrect, because observations indicate β < 1 (Sect. 4.2).
The magnetic field in the northern arm of IC 342 diverts not only in the vertical direction, but also in the disk plane. The ridge line of the polarization spiral arm as well as the magnetic pitch angle (Fig. 6) oscillate around the northern arm with similar periodicity. This gives indication for a large-scale, helically twisted flux tube, as predicted by models of the Parker loops under the Coriolis force (Shibata & Matsumoto 1991; Hanasz et al. 2002).
In the galaxy NGC 7479 (Fig. 24), two jets serve as bright polarized background sources. High-resolution observations revealed several reversals in RM on 1−2 kpc scale, originating in the foreground disk of the galaxy (Laine & Beck 2008), which may represent another case of a helically twisted field loop.
4.11. Large-scale field reversals
A large-scale field reversal exists between the central region and the disk in M 31 (Gießübel & Beck 2014) and in IC 342 (Beck 2015). A large-scale field reversal at about constant azimuthal angle across the whole galaxy disk was found in NGC 4414 (Soida et al. 2002). To fulfil the divergence-free condition, this reversal cannot occur in the same volume, but e.g. between disk and halo. Indication for a large-scale field reversal between disk and halo was also found in M 51 (Berkhuijsen et al. 1997; Fletcher et al. 2011; Mao et al. 2015). New observations and applying Faraday Synthesis (Sect. 3.6) are needed.
Large-scale field reversals between spiral arms, like that observed in the Milky Way (Fig. 26), have not been detected in external galaxies, although high-resolution images of Faraday rotation are available for many spiral galaxies. Possible reasons are discussed in Sect. 5.
Galaxies with massive bars have non-axisymmetic gas flows that interact with magnetic fields. The magnetic field lines in NGC 1097, one of the closest and brightest barred galaxies (Fig. 15), follow a pattern that resembles the flow of cold gas in a bar potential. As the gas rotates faster than the bar pattern of a galaxy, a shock occurs in the cold gas, which has a small sound speed, while the flow of warm, diffuse gas is only slightly compressed but sheared. The ordered field is also hardly compressed, probably coupled to the diffuse gas and strong enough to affect its flow (Beck et al. 2005). The ordered field is also strong in the upstream region (south of the center in Fig. 15), oriented almost perpendicularly to the bar and aligned with the dust filaments seen on the optical image in the background. The polarization pattern in barred galaxies can be used as a tracer of shearing gas flows in the sky plane and complements spectroscopic measurements of radial velocities.
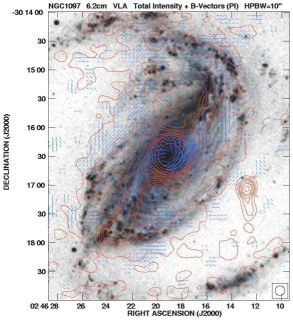 |
Figure 15. Total radio emission (contours) and B–vectors of the barred galaxy NGC 1097, observed at 6 cm wavelength with the VLA and smoothed to 10′′ resolution (from Beck et al. 2005). The background optical image is from Halton Arp. |
The central regions of barred galaxies are often sites of ongoing intense star formation and strong magnetic fields that can affect gas flows. NGC 1097 hosts a bright ring with about 1.5 kpc diameter and an active nucleus in its center (Fig. 16). The ordered field in the ring has a spiral pattern and extends to the nucleus. The orientation of the innermost spiral field agrees with that of the spiral dust filaments visible on optical images. Magnetic stress in the circumnuclear ring due to the strong total magnetic field (about 50 µG) can drive gas inflow (Balbus & Hawley 1998) at a rate of several solar masses per year, which is sufficient to fuel the activity of the nucleus (Beck et al. 2005). MHD modeling confirmed that magnetic fields can strongly enhance the mass gas inflow rate (Kim & Stone 2012).
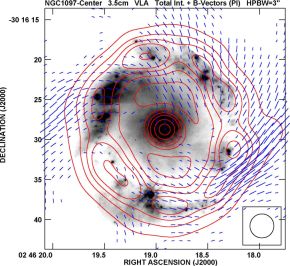 |
Figure 16. Total radio emission (contours) and B–vectors in the circumnuclear ring of the barred galaxy NGC 1097, observed at 3.5 cm wavelength with the VLA at 3′′ resolution. The background optical image is from the HST (from Beck et al. 2005). |
The central region of IC 342 hosts a bar of dust and cold gas with a wealth of molecular lines. In terms of size, dynamical mass, molecular mass, and star-formation rate, the nucleus of IC 342 is a potential twin of the Galactic centre (Meier 2014). While the central bar in total radio intensity coincides with the central bar in the CO line emission from molecular gas, the polarized emission reveals a double-lobe structure that is displaced from the CO bar (Fig. 17).
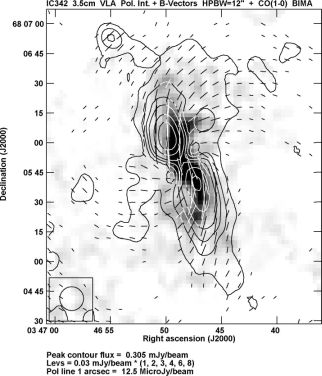 |
Figure 17. Polarized intensity and B–vectors in the central region of IC 342, observed at 3.5 cm wavelength with the VLA at 12′′ resolution, overlaid on a greyscale presentation of the CO(1-0) emission at 2.6 mm from the BIMA survey (Helfer et al. 2003). |
Hot gas, magnetic fields and cosmic rays in galaxy disks drive outflows that extend far beyond the galaxy disks seen at optical wavelengths and form thick disks or halos at radio wavelengths. 5 Radio polarization observations of several edge-on galaxies reveal vertical field components in the halo forming an X-shaped pattern, like in NGC 253 (Heesen et al. 2009b), NGC 891 (Fig. 18), NGC 4631 (Fig. 20), and NGC 5775 (Fig. 19), which may be related to outflows or to dynamo action (Moss et al. 2010) driven by such outflows.
 |
Figure 18. Total radio emission and B–vectors of the edge-on galaxy NGC 891, a galaxy similar to the Milky Way, observed at 3.6 cm wavelength with the Effelsberg telescope at 84′′ resolution (from Krause 2009). The background optical image is from the CFHT. (Copyright: MPIfR Bonn) |
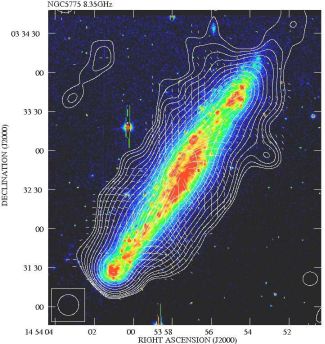 |
Figure 19. Total radio intensity and B–vectors of the edge-on galaxy NGC 5775, combined from observations at 3.6 cm wavelength with the VLA and Effelsberg telescopes at 16′′ resolution (from Soida et al. 2011). The background Hα image is from Tüllmann et al. (2000). (Copyright: MPIfR Bonn) |
The vertical profile of the total radio continuum emission gives information about the outflow speed. The profiles of five edge-on spiral galaxies observed with high resolution can be described by two exponential scale heights Hsyn, 300 ± 50 pc for the thin disk and 1.8 ± 0.2 kpc for the halo (Krause 2014). Neglecting the thermal contributions and assuming energy equipartition between total magnetic fields and total cosmic rays (Sect. 3.4), the scale heights of the total magnetic field are typically HB ≥ (3 + α) Hsyn ≃ 1.2 kpc for the thin disk and about 7 kpc for the halo, but probably larger due to energy losses of CREs. Because the average field strengths and hence the synchrotron lifetimes of CREs are different in different galaxies, the roughly constant halo scale heights indicate that outflow speeds increasing with the average field strength (and hence with the star-formation rate) may balance the smaller CRE lifetimes (Krause 2009).
Stronger magnetic fields in the central regions cause higher synchrotron loss of CREs, leading to the “dumbbell” shape of many radio halos, e.g. in NGC 253 (Heesen et al. 2009a) and NGC 4565 (Krause 2009). From the radio scale heights at several frequencies and the corresponding lifetimes of CREs (depending on synchrotron, inverse Compton and adiabatic losses) a wind speed of about 300 km/s was measured for the electrons in the halo of NGC 253 (Heesen et al. 2009a).
Galaxies without a detectable radio halo are rare. UGC 10288 shows discrete high-latitude radio features, but it does not have a global radio continuum halo (Irwin et al. 2013). No radio halo was found in M 31 (Berkhuijsen et al. 2013) and in NGC 7462 (Heesen et al., MNRAS, in press). These three galaxies have a star-formation rate that is probably too low to drive outflows.
On the other hand, exceptionally large and almost spherical radio halos are observed around interacting galaxies, namely NGC 4631 (Fig. 20) and the starburst galaxy M 82 (Adebahr et al. 2013; Reuter et al. 1994). A few magnetic spurs could be resolved in NGC 4631, connected to star-forming regions (Golla & Hummel 1994). These observations support the ideas of a strong galactic outflow (galactic wind), driven by regions of star formation in the disk, possibly supported by the interaction with neighbouring galaxies.
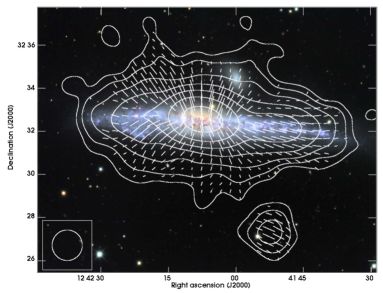 |
Figure 20. Total radio emission (contours) and B–vectors of the edge-on galaxy NGC 4631, observed at 3.6 cm wavelength with the Effelsberg telescope at 85′′ resolution (from Mora & Krause 2013). The background optical image is from the Digital Sky Survey. (Copyright: MPIfR Bonn) |
Above the central starburst region of NGC 253, an outwards-directed helical field of about 20 µG strength, extending to at least 1 kpc height, could be identified in the gas outflow cone with help of high-resolution RM mapping (Heesen et al. 2011a). This field may help to confine the outflow.
In summary, the occurrence of radio halos is governed by the competition between vertical transport of CREs by diffusion and/or convection (galactic wind) and energy losses of CREs, dominated by synchrotron loss. CRE transport can be characterized by the escape time tesc needed to reach the scale height H of the disk, beyond which the synchrotron emission significantly weakens. In case of diffusive transport, tesc ∝ (H2 / D), where D is the diffusion coefficient, while in case of convective transport tesc ∝ H / vwind, where vwind is the average wind speed.
For strong magnetic fields or slow winds or slow diffusion (tsyn ≪ tesc), the CREs cannot leave the disk and no radio halo develops, as in the case of M 31 (Berkhuijsen et al. 2013). For tsyn ≲ tesc, the scale height H of the synchrotron halo increases with distance from the center according to the increase in synchrotron lifetime (“dumbbell” halo) and with radio wavelength (H ∝ λ1/4 for diffusive or H ∝ λ1/2 for convective propagation). For weak fields or fast winds (tsyn > tesc), a large radio halo of elliptical or spherical shape is formed with a wavelength-independent scale height that is determined by the scale height of the total magnetic field and adiabatic losses of the expanding CRE flow. 6
4.14. Rudimentary spirals: flocculent and irregular galaxies
Flocculent galaxies have disks but no gaseous spiral arms. Nevertheless, magnetic spiral patterns have been observed in all flocculent galaxies so far, indicating that the α − Ω dynamo works independently of spiral density waves. Ordered magnetic fields with strengths similar to those in grand-design spiral galaxies have been detected in the flocculent galaxies M 33 (Tabatabaei et al. 2008), NGC 3521 and NGC 5055 (Knapik et al. 2000), and in NGC 4414 (Soida et al. 2002). The mean degree of polarization (corrected for the differences in spatial resolution) is also similar in grand-design and flocculent galaxies.
Radio continuum images of irregular, slowly rotating galaxies may reveal strong total magnetic fields, e.g. in the Magellanic-type galaxy NGC 4449 (Fig. 21), with a partly ordered field of about 7 µG strength, a spiral pattern in the northeast and a radial pattern in the central region (Chyży et al. 2000). Faraday rotation data shows that this ordered field is partly regular and the α − Ω dynamo is operating (Siejkowski et al. 2014).
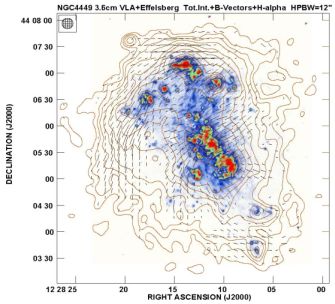 |
Figure 21. Total radio emission (contours) and B–vectors of the dwarf irregular galaxy NGC 4449, observed at 3.6 cm wavelength with the VLA at 12′′ resolution (from Chyży et al. 2000). The background Hα image is from Dominik Bomans (Bochum University). |
The Large and the Small Magellanic Clouds are the closest irregular galaxies at distances of 50 kpc and 60 kpc, respectively, interacting with the Milky Way and each other. Radio observations found the two galaxies to be weakly polarized (Haynes et al. 1991; Mao et al. 2012), with the exception of two highly polarized filaments in the southeast of the LMC. A study based on RM grids suggests that both galaxies host large-scale coherent fields, indicating that a large-scale dynamo also works under the less favourable conditions of slow ordered rotation (Mao et al. 2008; Mao et al. 2012). Due to their low potential well, low-mass galaxies are prone to outflows and galactic winds driven by star formation.
In dwarf irregular galaxies, the strengths of the total (turbulent) field are generally smaller than in spiral galaxies (Chyży et al. 2011), except for starburst dwarfs, e.g. NGC 1569 with 10−15 µG total field strength (Kepley et al. 2010), where star formation activity is sufficiently high for the operation of the small-scale dynamo. Consequently, dwarf galaxies form the low-luminosity tail of the radio–IR correlation for large galaxies (Chyży et al. 2011).
Spots of faint polarized emission were detected in dwarf irregular galaxies, but no large-scale regular fields so far (Heesen et al. 2011b), either due to a lack of telescope sensitivity or a lack of dynamo action. In classical α − Ω dynamo models, the dynamo number is too low for dynamo action because rotation is almost chaotic, while models including support of dynamo action by outflows predict α − Ω dynamos even in dwarf galaxies (Rodrigues et al. 2015).
4.15. Beyond spirals: interacting galaxies
Gravitational interaction between galaxies leads to asymmetric gas flows, compression, shear, enhanced turbulence and outflows that can be traced by observing magnetic fields in radio polarization. Magnetic fields can become aligned along the compression front or perpendicular to the velocity gradients. Such gas flows make turbulent fields highly anisotropic. Large-scale dynamos can be enhanced by ram pressure (Moss et al. 2014).
The classical interacting galaxy pair is NGC 4038/39, the “Antennae” (Chyży & Beck 2004). It shows bright, extended radio emission filling the whole system. In the interaction region between the galaxies, where star formation did not yet start, and at the northeastern edge of the system, the magnetic field is partly ordered, probably the result of compression and shearing motions along the tidal tail. Particularly strong, almost unpolarized emission comes from a region of violent star formation, hidden in dust. The average total magnetic field is stronger than in normal spirals, but the mean degree of polarization is unusually low, implying that the fields are tangled. The Antennae galaxies have been modeled by Kotarba et al. (2010), who could reproduce the main features observed in the radio image.
The total magnetic field in a sample of 16 systems in different interaction stages increases with advancing interaction, which indicates enhanced production of random magnetic fields (Drzazga et al. 2011). The strength of the ordered magnetic field are sensitive tools for revealing global galactic distortions. The pattern of the ordered field traces the orientation of gas flow in tidally stretched spiral arms and in tidal tails. Such outflows may have contributed to the magnetization of the intergalactic medium in the early cosmological epoch.
Interaction with a dense intergalactic medium also imprints unique signatures onto magnetic fields and thus onto the radio emission. The Virgo cluster is a location of especially strong interaction effects (Fig. 22), and almost all cluster galaxies observed so far show asymmetries of their polarized emission because the outer magnetic fields were compressed (Vollmer et al. 2007; Vollmer et al. 2013; Weżgowiec et al. 2007; Weżgowiec et al. 2012). Ordered fields are an excellent tracer of past interactions between galaxies or with the intergalactic medium.
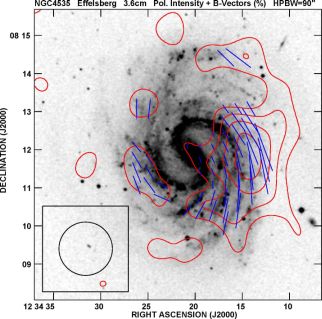 |
Figure 22. Polarized radio emission (contours) and B–vectors of the Virgo galaxy NGC 4535, observed at 3.6 cm wavelength with the Effelsberg telescope at 90′′ resolution (from Weżgowiec et al. 2012 and priv. comm.). The background optical image is from the Digital Sky Survey. |
4.16. Spiral galaxies with jets
Nuclear jets are observed in only a few spiral galaxies. These jets are weak and small compared to those of radio galaxies and quasars. Detection is further hampered by the fact that they emerge at some angle with respect to the disk, so that little interaction with the ISM occurs. If the nuclear disk is oriented at a large angle to the disk, the jet hits a large amount of ISM matter, CREs are accelerated in shocks, and the jet becomes radio-bright. However, not all jets are consistent with this morphology.
NGC 4258 is one of the rare cases where large radio jets of at least 15 kpc length are observed (Fig. 23). A nuclear disk is observed in water maser emission, has an inner radius of 0.13 pc and is seen almost edge-on (Greenhill et al. 1995). As the jets emerge perpendicular to the nuclear disk, they have to pass the galactic disk at a rather small angle. The magnetic field orientation is mainly along the jet direction. The equipartition field strength is about 300 µG at the resolution of about 100 pc (Krause & Löhr 2004), which is a lower limit due to energy losses of the CREs and the limited resolution.
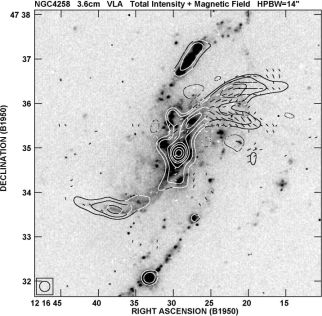 |
Figure 23. Total radio intensity (contours) and B–vectors of the jets in NNGC 4258, observed at 3.5 cm wavelength with the VLA at 14′′ resolution. The background Hα image is from the Hoher List Observatory of the University of Bonn (from Krause & Löhr 2004). |
The barred galaxy NGC 7479 also shows remarkable jet-like radio continuum features: bright, narrow, 12 kpc long in projection, and containing an aligned magnetic field (Fig. 24). The lack of any optical or near-infrared emission associated with the jets suggests that at least the outer parts of the jets are extraplanar features, although close to the disk plane. The equipartition strength is 35−40 µG for the total magnetic field and about 10 µG for the ordered magnetic field in the jets. According to Faraday rotation measurements, the large-scale regular magnetic field along the bar points towards the nucleus on both sides. Multiple reversals on scales of 1−2 kpc are detected, probably occurring in the galaxy disk in front of the eastern jet by anisotropic fields in the shearing gas flow in the bar potential.
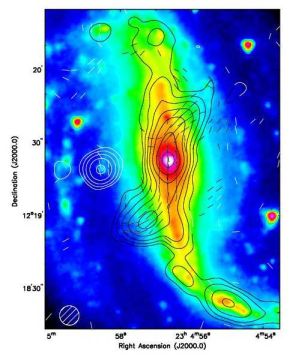 |
Figure 24. Total radio intensity (contours) and B–vectors of the jets in NGC 7479, observed at 3.5 cm wavelength with the VLA at 8′′ resolution. The background shows a Spitzer/IRAC image at 3.6 µm (NASA/JPL-Caltech/Seppo Laine) (from Laine & Beck 2008). |
Highly polarized radio emission from kpc–size jets has also been detected in NGC 3079 (Cecil et al. 2001), with the field orientations perpendicular to the jet's axis, and in the outflow lobes of the Circinus Galaxy (Elmouttie et al. 1995). Two members of the Virgo cluster, NGC 4388 and NGC 4438, have elongated radio features emerging from the active Seyfert–type nuclei and extending roughly perpendicular to the planes of the disks (Hummel & Saikia 1991). Detailed images including polarization are forthcoming as results of the CHANG-ES survey of edge-on galaxies (Irwin et al. 2012).
Jets in spiral galaxies may be more frequent than the available radio observations suggest. Future low-frequency observations will help to search for weak synchrotron emission from interface regions between the jets and the low-density halo gas.
4 The nonlinearity of the Kennicutt-Schmidt law can be interpreted as a dependence of the star-formation efficiency (SFE) on the stellar mass surface density (Shi et al. 2011). Interestingly, effects of the magnetic field on the SFE have not been investigated so far. Back.
5 As a definition of how to distinguish “thick disk” from “halo” is missing, “halo” is used in the following. Back.
6 Detailed models of radio halos are presented in Lerche & Schlickeiser (1982a); Lerche & Schlickeiser (1982b). Back.