


Inference is the method by which we translate experimental/observational information into constraints on our mathematical models. The model is a representation of the physical processes that we believe are relevant to the quantities we plan to observe. To be useful, the model must be sufficiently sophisticated as to be able to explain the data, and simple enough that we can obtain predictions for observational data from it in a feasible time. At present these conditions are satisfied in cosmology, with the best models giving an excellent representation of that data, though the computation of theoretical predictions for a representative set of models is a supercomputer class problem. Particularly valued are models which are able to make distinctive predictions for observations yet to be made, though Nature is under no obligation to behave distinctively.
The data which we obtain may be subject only to experimental uncertainty, or they may also have a fundamental statistical uncertainty due to the random nature of underlying physical processes. Both types of data arise in cosmology. For instance, the present expansion rate of the Universe (the Hubble constant), could in principle be measured to near-arbitrary accuracy with sufficiently advanced instrumentation. By contrast, the detailed pattern of cosmic microwave anisotropies, as measured by WMAP, is not believed to be predictable even in principle, being attributed to a particular random realization of quantum processes occurring during inflation [2]. Observers at different locations in the Universe see different patterns in the CMB sky, the cosmological information being contained in statistical measures of the anisotropies such as the power spectrum. Observers at any particular location, such as ourselves, can witness only our own realization and there is an inherent statistical uncertainty, cosmic variance, that we cannot overcome, but which fortunately can be modelled and incorporated in addition to measurement uncertainty.
A model will typically not make unique predictions for observed quantities; those predictions will instead depend on some number of parameters of the model. Examples of cosmological parameters are the present expansion rate of the Universe, and the densities of the various constituents such as baryons, dark matter, etc. Such parameters are not (according to present understanding, anyway) predictable from some fundamental principle; rather, they are to be determined by requiring that the model does fit the data to hand. Indeed, determining the values of such parameters is often seen as the primary goal of cosmological observations, and Chapter 3 is devoted to this topic.
At a more fundamental level, several different models might be proposed as explanations of the observational data. These models would represent alternative physical processes, and as such would correspond to different sets of parameters that are to be varied in fitting to the data. It may be that the models are nested within one another, with the more complex models positing the need to include extra physical processes in order to explain the data, or the models may be completely distinct from one another. An example of nested models in cosmology is the possible inclusion of a gravitational wave contribution to the observed CMB anisotropies. An example of disjoint models would be the rival explanations of dark energy as caused by scalar field dynamics or by a modification to the gravitational field equations. Traditionally, the choice of model to fit to the data has been regarded as researcher-driven, hopefully coming from some theoretical insight, with the model to be validated by some kind of goodness-of-fit test. More recently, however, there has been growing interest in allowing the data to distinguish between competing models. This topic, model selection or model comparison, is examined in Chapter 4.
The comparison of model prediction to data is, then, a statistical inference problem where uncertainty necessarily plays a role. While a variety of techniques exist to tackle such problems, within cosmology one paradigm dominates — Bayesian inference. This article will therefore focus almost exclusively on Bayesian methods, with only a brief account of alternatives at the end of this section. The dominance of the Bayesian methodology in cosmology sets it apart from the traditional practice of particle physicists, though there is now increasing interest in applying Bayesian methods in that context (e.g. Ref. [5]).
The Bayesian methodology goes all the way back to Thomas Bayes and his theorem, posthumously published in 1763 [6], followed soon after by pioneering work on probability by Laplace. The technical development of the inference system was largely carried out in the first half of the 20th century, with Jeffreys' textbook [7] the classic source. For several decades afterwards progress was held up due to an inability to carry out the necessary calculations, and only in the 1990s did use of the methodology become widespread with the advent of powerful multiprocessor computers and advanced calculational algorithms. Initial applications were largely in the fields of social science and analysis of medical data, the volume edited by Gilks et al. [8] being a particularly important source. The publication of several key textbooks in the early 21st century, by Jaynes [9], MacKay [10] and Gregory [11], the last of these being particularly useful for physical scientists seeking to apply the methods, cemented the move of such techniques to the mainstream. An interesting history of the development of Bayesianism is given in Ref. [12].
The essence of the Bayesian methodology is to assign probabilities to all quantities of interest, and to then manipulate those probabilities according to a series of rules, amongst which Bayes theorem is the most important. The aim is to update our knowledge in response to emerging data. An important implication of this set-up is that it requires us to specify what we thought we knew before the data was obtained, known as the prior probability. While all subsequent steps are algorithmic, the specification of the prior probability is not, and different researchers may well have different views on what is appropriate. This is often portrayed as a major drawback to the Bayesian approach. I prefer, however, to argue the opposite — that the freedom to choose priors is the opportunity to express physical insight. In any event, one needs to check that one's result is robust under reasonable changes to prior assumptions.
An important result worth bearing in mind is a theorem of Cox [13], showing that Bayesian inference is the unique consistent generalization of Boolean logic in the presence of uncertainty. Jaynes in particular sees this as central to the motivation for the Bayesian approach [9].
In abstract form, Bayes theorem can be written as
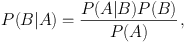 |
(1) |
where a vertical line indicates the conditional probability, usually read as ‘the probability of B given A'. Here A and B could be anything at all, but let's take A to be the set of data D and B to be the parameter values θ (where θ is the N-dimensional vector of parameters being varied in the model under consideration), hence writing
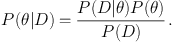 |
(2) |
In this expression, P(θ) is the prior probability,
indicating what we thought the probability of different values of
θ was before we employed the data D. One of our objectives
is to use this equation to obtain the posterior probability of the
parameters given the data, P(θ|D). This is achieved by
computing the likelihood P(D|θ), often
denoted  (θ) with the
dependence on the dataset left implicit.
(θ) with the
dependence on the dataset left implicit.
2.3. Alternatives to Bayesian inference
The principal alternative to the Bayesian method is usually called the frequentist approach, indeed commonly a dichotomy is set up under which any non-Bayesian method is regarded as frequentist. The underpinning concept is that of sampling theory, which refers to the frequencies of outcomes in random repeatable experiments (often caricatured as picking coloured balls from urns). According to MacKay [10], the principal difference between the systems is that frequentists apply probabilities only to random variables, whereas Bayesians additionally use probabilities to describe inference. Frequentist analyses commonly feature the concepts of estimators of statistical quantities, designed to have particular sampling properties, and null hypotheses which are set up in the hope that data may exclude them (though without necessarily considering what the preferred alternative might be).
An advantage of frequentist methods is that they avoid the need to specify the prior probability distribution, upon which different researchers might disagree. Notwithstanding the Bayesian point-of-view that one should allow different researchers to disagree on the basis of prior belief, this means that the frequentist terminology can be very useful for expressing results in a prior-independent way, and this is the normal practice in particle physics.
A drawback of frequentist methods is that they do not normally distinguish the concept of a model with a fixed value of a parameter, versus a more general model where the parameter happens to take on that value (this is discussed in greater detail below in Section 4), and they find particular difficulties in comparing models which are not nested.