3. COSMOLOGICAL PARAMETER ESTIMATION

3.1. Goals and methodology

In cosmological parameter estimation, we take for granted that we have a dataset D, plus a model with parameter vector θ from which we can extract predictions for those data, in the form of the likelihood (θ) ≡ P(D|θ). Additionally, we will have a prior distribution for those parameters, representing our knowledge before the data was acquired. While this could be a distribution acquired from analyzing some previous data, more commonly cosmologists take the prior distribution to be flat, with a certain range for each parameter, and reanalyze from scratch using a compilation of all data deemed to be useful.

Our aim is then to figure out the parameter values which give the best fit to the data, or, more usefully, the region in parameter space within which the fit is acceptable, i.e. to find the maximum likelihood value and explore the shape of the likelihood in the region around it. In many cases one can hope that the likelihood takes the form of a multi-variate gaussian, at least as long as one doesn't stray too far from the maximum.

The task then is to find the high-likelihood regions of the function (θ), which sounds straightforward. However, there are various obstacles

• The likelihood function may be extremely sharply peaked, and it may have several maxima masquerading as the true maximum.
• The parameter space may have a high dimensionality, cosmological examples often having 6 to 10 parameters independently varying.
• There may be parameter degeneracies, where likelihood varies only weakly, or not at all, along some direction in parameter space.
• The evaluations of the likelihood may be computationally demanding, either in generating the theoretical predictions from the model, or in computing the likelihood of those predictions. A typical likelihood evaluation in a cosmological calculation involving CMB anisotropies is a few seconds of CPU time.

In combination, these seriously obstructed early data analysis efforts, even when the dataset was fairly limited, because available computer power restricted researchers to perhaps 10⁵ to 10⁶ likelihood evaluations. Once beyond five or six parameters, which is really the minimum for an interesting comparison, brute-force mapping of the likelihood on a grid of parameters becomes inefficient, as the resolution in each parameter direction becomes too coarse, and anyway too high a fraction of computer time ends up being used in regions where the likelihood turns out to be too low to be of interest.

This changed with a paper by Christensen and Meyer [14], who pointed out that problems of this kind are best tackled by Monte Carlo methods, already extensively developed in the statistics literature, e.g. Ref. [8]. Subsequently, Lewis and Bridle wrote the CosmoMC package [15], implementing a class of Monte Carlo methods for cosmological parameter estimation. The code has been very widely adopted by researchers, and essentially all cosmological parameter estimation these days is done using one of a variety of Monte Carlo methods.

3.2. Monte Carlo methods

Monte Carlo methods are computational algorithms which rely on random sampling, with the algorithm being guided by some rules designed to give the desired outcome. An important subclass of Monte Carlo methods are Markov Chain Monte Carlo (MCMC) methods, defined as those in which the next ‘step' in the sequence depends only upon the previous one. The sequence of steps is then known as a Markov chain. Each step corresponds to some particular value of the parameters, for which the likelihood is evaluated. The Markov chain can therefore be viewed as a series of steps (or jumps) around the parameter space, investigating the likelihood function shape as it goes.

You may find it convenient to visualize the likelihood surface as a mountainous landscape with one dominant peak. The simplest task that such a process could carry out would be to find the maximum of the likelihood: choose a random starting point, propose a random jump to a new point, accept the jump only if the new point has a higher likelihood, return to the proposal step and repeat until satisfied that the highest point has been found. Even this simple algorithm obviously needs some tuning: if the steps are too large, the algorithm may soon find it difficult to successfully find a higher likelihood point to jump to, whereas if they are small the chain may get stuck in a local maximum which is not the global maximum. That latter problem may perhaps be overcome by running a series of chains from different starting points.

Anyway, the maximum itself is not of great interest; what we want to know is the region around the maximum which is compatible with the data. To do this, we desire an algorithm in which the Markov chain elements correspond to random samples from the posterior parameter distribution of the parameters, i.e. that each chain element represents the probability that those particular parameter values are the true ones. The simplest algorithm which achieves this is the Metropolis–Hastings algorithm, which is a remarkably straightforward modification of the algorithm described in the previous paragraph.

3.2.1. Metropolis–Hastings algorithm

The Metropolis–Hastings algorithm is as follows:

1. Choose a starting point within the parameter space.
2. Propose a random jump. Any function can be used to determine the probability distribution for the length and direction of the jump, as long as it satisfies the ‘detailed balance' condition that a jump back to the starting point is as probable as the jump away from it. This is most easily done using a symmetric proposal function, e.g. a multivariate gaussian about the current point. Evaluate the likelihood at the new point, and hence the probability by multiplying by the prior at that point. [If the prior is flat, the probability and likelihood become equivalent.]
3. If the probability at the new point is higher, accept the jump. If it is lower, we accept the jump with a probability given by the ratio of the probabilities at the new and old point. If the jump is not accepted, we stay at the same point, creating a duplicate in the chain.
4. Repeat from Step 2, until satisfied that the probability distribution is well mapped out. This may be done for instance by comparing several chains run from different starting points, and/or by using convergence statistics amongst which the Gelman–Rubin test [16, 8] is the most commonly used.

By introducing a chance of moving to a lower probability point, the algorithm can now explore the shape of the posterior in the vicinity of the maximum. The generic behaviour of the algorithm is to start in a low likelihood region, and migrate towards the high likelihood ‘mountains'. Once near the top, most possible jumps are in the downwards direction, and the chain meanders around the maximum mapping out its shape. Accordingly, all the likelihood evaluations, which is where the CPU time is spent, are being carried out in the region where the likelihood is large enough to be interesting. The exception is the early stage, which is not representative of the posterior distribution as it maintains a memory of the starting position. This ‘burn-in' phase is then deleted from the list of chain points.

Although any choice of proposal function satisfying detailed balance will ultimately yield a chain sampling from the posterior probability distribution, in practice, as with the simple example above, the algorithm needs to be tuned to work efficiently. This is referred to as the convergence of the chain (to the posterior probability). The proposal function should be tuned to the scale of variation of the likelihood near its maximum, and if the usual choice of a gaussian is made its axes should ideally be aligned to the principal directions of the posterior (so as to be able to navigate quickly along parameter degeneracies). Usually, a short initial run is carried out to roughly map out the posterior distribution which is then used to optimize the proposal function for the actual computation. ¹ The resulting acceptance rate of new points tends to be around 25%.

The upshot of this procedure is a Markov chain, being a list of points in parameter space plus the likelihood/posterior probability at each point. A typical cosmological example may contain 10⁴ to 10⁵ chain elements, and some collaborations including WMAP make their chains public. There is usually some short-scale correlation of points along the chain due to the proposal function; some researchers ‘thin' the chain by deleting elements to remove this correlation though this procedure appears unnecessary. By construction, the elements correspond to random samples from the posterior, and hence a plot of the point density maps it out.

The joy of having a chain is that marginalization (i.e. figuring out the allowed ranges of a subset of the full parameter set, perhaps just one parameter) becomes trivial; you just ignore the other parameters and plot the point density of the one you are interested in. By contrast, a grid evaluation of the marginalized posterior requires an integration over the uninteresting directions.

Figure 2 shows a typical outcome of a simple MCMC calculation.

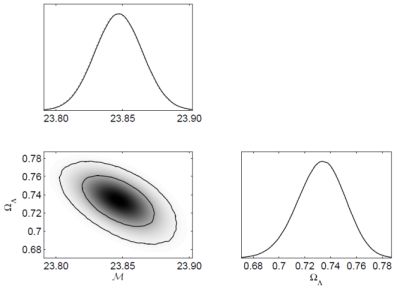Figure 2. Output of a very simple two-parameter MCMC analysis. The data set is a combination of supernova, CMB, and galaxy correlation data, and the two parameters are the cosmological constant ΩΛ and the standardized supernova brightness . The two-dimensional distribution is in the bottom left and the marginalized single-parameter constraints in the other two boxes. In this case, both parameters have accurately gaussian distributions and are correlated. [Figure reproduced from Ref. [17].]

• Importance sampling. If new data becomes available, rather than computing new chains from scratch one can importance sample existing chains, by reweighting the elements according to the new likelihood [15]. One can also use importance sampling to study the effect of varying the prior. These operations mean that the points now have non-integer weights, but this creates no new issue of principle. However importance sampling may result in an insufficient density of points in the new preferred region, making the sampling of the posterior noisier than would be possible with new chains.
• Bayesian complexity. This quantity measures the number of parameters actually constrained by the data in hand [18, 19], which may be less than the number of parameters of the model, either because overall the data are poorly constraining, or because of specific parameter degeneracies leaving some parameter combinations unconstrained. It can also be used to determine a semi-Bayesian model selection statistic known as the Deviance Information Criterion, discussed briefly in Section 4.5

3.2.2. Other sampling algorithms

Metropolis–Hastings achieves the desired goal, but may struggle to do so efficiently if it is difficult to find a good proposal function or if the assumption of a fixed proposal function proves disadvantageous. This has tended not to be a problem in cosmological applications to date, but it is nevertheless worthwhile to know that there are alternatives which may be more robust. Some examples, all discussed in MacKay's book [10], are

• Slice sampling: This method allows the proposal function to change during the calculation, tuning itself to an appropriate scale, though there is an additional computational cost associated with enforcing the detailed balance condition. The steps are made in a single parameter direction at a time, hence the name, and cycle through the parameter directions either sequentially or randomly. Slice sampling is implemented in CosmoMC as an alternative to Metropolis–Hastings, as are some other more specialized sampling algorithms.
• Gibbs sampling: This relies on obtaining a proposed step by sampling from conditional probability distributions, e.g. to step in the θ₁ direction we sample from P(θ₁|θ₂) and vice versa. It turns out that such proposals are always accepted, enhancing the efficiency. The method can however struggle to make progress along highly correlated parameter directions, traversing the diagonal through a series of short steps parallel to the axes.
• Hamiltonian sampling: This more sophisticated approach uses an analogy with Hamiltonian dynamics to define a momentum from derivatives of the likelihood. The momentum associated with a point enables large proposal steps to be taken along trajectories of constant ‘energy' and is particularly well adapted to very high dimensionality problems. See Refs. [20, 21] for cosmological applications.

3.2.3. Machine learning

The slow likelihood evaluations, stemming mainly from the time needed to predict observational quantities such as the CMB power spectra from the models, remain a significant stumbling block in cosmological studies. One way around this may be to use machine learning to derive accurate theoretical predictions from a training set, rather than carry out rigorous calculations of the physical equations at each parameter point. Two recent attempts to do this are PICO [22] and CosmoNet [23], the former also allowing direct estimation of the WMAP likelihood from the training set. This is a promising method, though validation of the learning output when new physical processes are included may still mean that many physics-based calculations need to be done.

3.2.4. Overview

In conclusion, cosmological parameter estimation from data is increasingly regarded as a routine task, albeit one that requires access to significant amounts of computing resource. This is principally attributed to the public availability of the CosmoMC package, and the continued work by its authors and others to enhance its capabilities. On the theoretical side, an impressive range of physical assumptions are supported, and many researchers have the expertise to modify the code to further broaden its range. On the observational side, researchers have recognized the importance of making their data available in formats which can readily be ingested into MCMC analyses. The WMAP team were the first to take this aspect of delivery very seriously, by publically releasing the ‘WMAP likelihood code' at the same time as their science papers, allowing cosmologists everywhere to immediately explore the consequences of the data for their favourite models. Indeed, I would argue that by now the single most important product of an observational programme would be provision of a piece of software calculating the likelihood as a function of input quantities (e.g. the CMB power spectra) computable by CosmoMC.

3.3. Uncertainties, biases and significance

The significance with which results are endowed appears to be strongly dependent on the science community obtaining them. At one extreme lies particle physics experimentalists, who commonly set a ‘five-sigma' threshold to claim a detection (in principle, for gaussian uncertainties, corresponding to 99.99994% probability that the result is not a statistical fluke). By contrast, astrophysicists have been known to get excited by results at or around the ‘two-sigma' level, corresponding to 95.4% confidence for a gaussian. At the same time, there is clearly a lot of skepticism as to the accuracy of confidence limits; some possibly apocryphal quotes circulating in the data analysis community include “Once you get to three-sigma you have about a half chance of being right.” and “95% of 95% confidence results do not turn out to be right; if anything 95% of them turn out to be wrong”.

There are certainly good reasons to think that results are less secure than the stated confidence from a likelihood analysis would imply. Amongst these are

• In realistic cases, the probability may not fall as fast as a gaussian in the tails of the distribution even if accurately gaussian near the peak.
• There may be unmodelled systematic errors. The natural trend in a maturing observational field is to be initially dominated by statistical uncertainty, but as instrumental accuracy improves to then reach a systematic floor where it becomes difficult or impossible to model extraneous physical effects (e.g. population evolution in supernovae which one is planning to use as standard candles over cosmic epochs).
• The likelihood function may be uncertain in a way not included in the quoted uncertainty. For instance there are now several different treatments of the WMAP likelihood, differing in the way the beam profiles, source subtraction, or low multipole likelihoods are calculated.
• The researchers may, consciously or otherwise, have adopted a model motivated by having seen the data, and then attempted to verify it from the same data. It has recently been claimed that this problem is widespread in the neuroscience field [24], with the authors of that study suspecting the issue extends to other disciplines. An example of this would be to spot an unusual feature in, say, a cosmic microwave background map, and then attempt to assess the probability of such a feature using Monte Carlo simulations. This ignores the fact that there may have been any number of other no more unlikely features, that weren't seen in the data. Consider the well-publicized appearance of Stephen Hawking's initials in the WMAP maps, obviously massively improbable a priori but nonetheless visible in Fig. 1 (in blue, just above the middle axis, somewhat left of center).
• Publication bias: positive results are more likely to get published than negative ones, e.g. the 95% confidence result you just read about arose from one of 20 studies, the other 19 of which generated null results. This is widely recognized in the medical statistics community, ² leading to introduction of costly treatments that may be ineffective or even harmful. In this context, the additional problem may exist that trials are funded by large companies whose profitability depends on the outcome, and who may be in a position to influence whether they are published. In cosmology, this may be a particular problem for cosmic non-gaussianity studies, where many different independent tests can be carried out.
• Model uncertainty: the possibility of different models, rather than just parameter values, describing the data has not be consistently allowed for.

I'm aware of situations where all of these have been important, and in my view 95% confidence is not sufficient to indicate a robust result. This appears to increasingly be the consensus in the cosmology community, perhaps because too much emphasis was put on two 95% confidence level results in the first-year WMAP data (a high optical depth and running of the spectral index) which lost support in subsequent data releases.

On the other hand, ‘five-sigma' may be rather too conservative, intended to give a robust result in all circumstances. In reality, the confidence level at which a result becomes significant should depend on the nature of the model(s) under consideration, and the nature of the data obtained. Some guidance on where to draw the line may be obtained by exploring the issue of model uncertainty, the topic of the next section.

¹ One can also help things along by using variables which respect known parameter degeneracies in the data, e.g. that the CMB data is particularly good at constraining the angular-diameter distance to the last-scattering surface through the position of the peaks. Back.

² Ioannidis [25] goes so far as to claim a proof that most published results are false, publication bias being partly responsible. Back.