


Over the past few decades, the very meaning of the phrase “dark matter” has evolved considerably. Today, this phrase is most frequently used as the name – a proper noun – of whatever particle species accounts of the bulk of our Universe's matter density. When a modern paper discusses the distribution of dark matter, or the impact of dark matter on structure formation, or the prospects for detecting dark matter with a gamma-ray telescope, the reader does not have to ask themselves whether the authors might have in mind white dwarfs, neutron stars, or cold clouds of gas – they don't. This is in stark contrast to the earlier usage of the phrase, in which the word “dark” was a mere adjective, and “dark matter” included all varieties of astrophysical material that happened to be too faint to be detected with available telescopes.
This linguistic transition reflects a larger change that has taken place over the past several decades within the astrophysics and particle physics communities. And although this transformation was driven and initiated by new scientific results and understanding, it also reflects a sociological change in the underlying scientific culture. Half a century ago, cosmology was something of a fringe-science, perceived by many astronomers and particle physicists alike to have little predictive power or testability. This can be easy to forget from our modern vantage point in the age of precision cosmology. Furthermore, prior to the last few decades, particle physicists did not often study or pursue research in astrophysics, and most astrophysicists learned and knew little about particle physics. As a result, these scientists did not frequently contribute to each other's fields of research. When Fermilab founded its theoretical astrophysics group in 1983, for example, the decision to do so was seen by many as a radical departure from the lab's particle physics mission. From the perspective of many particle physicists in the early 1980s, it was not obvious what astrophysics had to do with the questions being asked by particle physics. This view is shared by few today. As an illustration, we need only to note that the report of the US Particle Physics Project Prioritization Panel (P5) describes the “Cosmic Frontier”, along with the Energy and Intensity Frontiers, as co-equal areas of inquiry within the larger field of particle physics.
From our contemporary perspective, it can be easy to imagine that Fritz Zwicky, Vera Rubin, and the other early dark matter pioneers had halos of weakly interacting particles in mind when they discussed dark matter. In reality, however, they did not. But over time, an increasing number of particle physicists became interested in cosmology, and eventually in the problem of dark matter. By the late 1980s, the hypothesis that the missing mass consists of one or more yet-unknown subatomic particle species had gained enough support to become established as the leading paradigm for dark matter. As alternatives were ruled out one-by-one (see Chapters VI and VII), this view came to be held almost universally among both particle physicists and astrophysicists, as well as among their new and now increasingly common hybrids – the particle-astrophysicists.
When one considers the dark matter problem from the perspective of the standard model of particle physics, the three neutrinos clearly stand out. Unlike all other known particle species, the neutrinos are stable – or at least very long lived – and do not experience electromagnetic or strong interactions. These are essential characteristics for almost any viable dark matter candidate. And although we know today that dark matter in the form of standard model neutrinos would be unable to account for our Universe's observed large scale structure, these particles provided an important template for the class of hypothetical species that would later be known as WIMPs – weakly interacting massive particles. In this way, standard model neutrinos served as an important gateway particle, leading astrophysicists and particle physicists alike to begin their experimentation with a variety of other, more viable, particle dark matter candidates. And although the first scientists to consider the role of neutrinos in cosmology did not have the dark matter problem in mind – many being unaware that there was any such problem to solve – their work helped to establish the foundations that the field of particle dark matter would later be built upon.
The earliest discussion of the role of neutrinos in cosmology appeared in a 1966 paper by S. S. Gershtein and Ya. B. Zeldovich [132]. To many scientists working in fields of cosmology and particle-astrophysics, it will be no surprise to see Zeldovich's name attributed to this pioneering work. Yakov Borisovich Zeldovich was an utterly prolific and versatile physicist, making major contributions to the fields of material science, nuclear physics (including the Soviet weapons program), particle physics, relativity, astrophysics, and cosmology. In terms of research at the interface between particle physics and cosmology, it can sometimes seem like Zeldovich did almost everything first.
In the early 1960s, Zeldovich was one of only a handful of particle physicists who were also thinking about problems in cosmology. During this period, he made early contributions to black hole thermodynamics, recognized that accretion disks around black holes could power quasars, discussed the possibility of primordial black holes, and studied the problem of how the large scale structure of the Universe formed. He is probably most famous for his paper with Rashid Sunyaev, which predicted that the cosmic microwave background would be distorted by its inverse Compton scattering with high-energy electrons in galaxy clusters [306]. This so-called “Sunyaev-Zeldovich effect” was observed for the first time in 1983, and continues to be of considerable importance in modern cosmology. So sweeping were Zeldovich's contributions to cosmology, that upon being introduced, Stephen Hawking is said to have expressed to him, “Before I met you, I believed you to be a collective author, like Bourbaki 5.”
In their 1966 paper, Zeldovich and Gershtein considered the production of neutrinos under the conditions that existed shortly after the Big Bang. Making use of the knowledge of the newly discovered three degree cosmic microwave background [242], they predicted how many electron and muon neutrinos would have existed in thermal equilibrium in the early Universe, and at what temperature those particles would have ceased to efficiently self-annihilate, leading to a population of neutrinos that survived as a thermal relic 6. Considering how the density of those neutrinos would impact the expansion history of the Universe, and comparing that to existing estimates of the Hubble constant and the age of the oldest observed stars, Zeldovich and Gershtein concluded that the masses of the electron and muon neutrinos must each be less than approximately 400 eV; if they had been heavier, the neutrinos would have unacceptably slowed, or even reversed, the rate of cosmic expansion. For the muon neutrino, this result represented an improvement of three orders of magnitude over the previously existing upper limits.
Looking back at this result from a modern perspective, we see the seeds of particle dark matter, and even WIMPs. In particular, Zeldovich and Gershtein showed that a neutrino species with a mass of a few tens of eV or greater would come to dominate the energy density of the Universe. But there was no mention in their paper of any missing mass that these neutrinos might be able to account for; they only required that the density of the relic neutrinos not be so high as to cause the expansion rate of the Universe to slow down faster than observed.
This is essentially the same perspective that was expressed years later, when papers on this topic began to appear in the West. The first of these papers appeared in 1972, in which Ram Cowsik and J. McClelland used an approach similar to Zeldovich and Gershtein's to derive an upper limit of 8 eV on the mass of a single (Dirac) neutrino species [82] (see also Ref. [207]). If it had not been for this paper, one might be tempted to conclude that interest in this topic would have developed much sooner among American and Western European scientists if word of Zeldovich and Gershtein's work had reached them earlier.
But the paper by Cowsik and McClelland (who were both at the University of California, Berkeley, at the time) seems to disprove this counterfactual. Even after the appearance of this paper, there was no discernible rush to further explore the role of neutrinos (or other thermal relics) in the early Universe.
Eventually, however, interest in neutrino cosmology did begin to pick up. In 1976, A. S. Szalay and G. Marx published a paper that not only derived an upper limit on neutrino masses from cosmology, but also discussed the possibility that ∼10 eV neutrinos might make up the “missing mass” in the Universe, and in galaxy clusters. Then, a few years later, a sequence of related papers appeared in rapid succession. In a paper received in April of 1977, Piet Hut presented a limit on the neutrino mass from cosmological considerations, ruling out masses in the range of 120 eV to 3 GeV [164]. In contrast to the authors of the preceding papers, Hut pointed out that quite heavy neutrinos (mν> 3 GeV) would be produced in the Big Bang with an abundance that would not overclose the Universe. Only about a week later, Ben Lee and Steven Weinberg submitted a paper that included a very similar lower bound (mν > 2 GeV) [194]. In the same month, a paper by K. Sato and H. Kobayashi [278] presented similar conclusions, and another by Duane Dicus, Edward “Rocky” Kolb and Vigdor Teplitz pointed out that such bounds could be evaded if neutrinos were unstable [91]. A month later, a new paper by Zeldovich (with M. I. Vysotskii and A. D. Dolgov) appeared, updating their own cosmological constraints on neutrino mass [322].
Despite the very interesting and important results of these papers, it is notable that most of them did not attempt to address, or even acknowledge, the possibility that neutrinos could account for the missing mass observed by astronomers on galactic and cluster scales. Exceptions to this include the 1976 paper of Szalay and Marx, and the 1977 paper of Lee and Weinberg, whose final sentence reads as follows [194]:
Of course, if a stable heavy neutral lepton were discovered with a mass of order 1-15 GeV, the gravitational field of these heavy neutrinos would provide a plausible mechanism for closing the universe.
While this is still a long way from acknowledging the dynamical evidence for dark matter, it was an indication that physicists were beginning to realize that weakly interacting particles could be very abundant in our Universe, and may have had an observable impact on its evolution. The connection between particle physics and the missing mass problem did gradually become more appreciated over the years to come. In 1978, for example, a paper by James Gunn, Ben Lee, Ian Lerche, David Schramm, and Gary Steigman included the following statement in their abstract [144]:
... such a lepton is an excellent candidate for the material in galactic halos and for the mass required to bind the great clusters of galaxies.
By the end of the decade, a number of scientists – including Zeldovich and his Moscow group [99, 100, 344] – had begun to argue in favor of neutrinos as dark matter. Interest in this possibility grew considerably in and after 1980, when a group studying tritium beta decay reported that they had measured the mass of the electron anti-neutrino (and presumably also the electron neutrino) to be approximately 30 eV [201]. With a mass of this value, neutrinos would be expected to have played a very significant role in cosmology. And although this “discovery” was eventually refuted, it motivated many particle physicists to further investigate the cosmological implications of their research, and encouraged many astrophysicists to consider the possibility that the dark matter halos surrounding galaxies and galaxy clusters might not be made up of faint stars or other astrophysical objects, but instead might consist of a gas of non-baryonic particles.
By the middle of the 1980s, a new tool had come into use that would put neutrino dark matter to the test. This tool — numerical simulations — could be used to predict how large numbers of dark matter particles would evolve under the force of gravity in an expanding Universe, and thus was able to assess the cosmological role and impact of dark matter particles on the formation of large scale structure. Importantly, such tests could be used to discriminate between different dark matter candidates, at least in some cases.
The primary characteristic of a given particle dark matter candidate that can be probed by numerical simulations is whether it was relativistic (hot) or non-relativistic (cold) during the epoch of structure formation 7. Standard model neutrinos, being very light thermal relics, are predicted to emerge from the early Universe with a highly relativistic velocity distribution, and thus represent an example of hot dark matter [281, 240]. Simulations have shown that hot dark matter particles would tend to collapse and form very large structures first, and only later go on to form smaller (i.e. galaxy-sized) halos through the fragmentation of larger halos. In contrast to this “top-down” sequence of structure formation, cold dark matter particles form structures through a “bottom-up” sequence, beginning with the smallest halos, which go on to form larger halos through a succession of mergers.
From these early simulations, it quickly became clear that hot and cold dark matter lead to very different patterns of large scale structure. By comparing the results of these simulations with those of galaxy surveys (in particular the CfA survey, which was the first extensive 3D survey of galaxies in the local Universe [85]), it was determined that standard model neutrinos – or any other examples of hot dark matter – could not account for most of the dark matter in the Universe [333]. In their 1983 paper, Simon White, Carlos Frenk and Marc Davis make the following statement about a neutrino-dominated Universe [333]:
We find [the coherence length] to be too large to be consistent with the observed clustering scale of galaxies... The conventional neutrino-dominated picture appears to be ruled out.
We will discuss numerical simulations, and their role in the history of dark matter, in greater detail in Sec. VIII C.
As it became accepted that standard model neutrinos could not make up most of the Universe's dark matter 8, it also became clear that there must exist at least one currently unknown particle species that makes up the missing mass. But although standard model neutrinos were far too light and hot to make up the dark matter, this new information did not preclude the possibility that other types of neutrino-like particles might make up this elusive substance (see, for example, Ref. [224]). In 1993, Scott Dodelson and Lawrence Widrow proposed a simple scenario in which an additional neutrino species, without the electroweak interactions experienced by standard model neutrinos, could be produced in the early Universe and realistically make up the dark matter [98]. Other than through gravity, the particles envisioned by Dodelson and Widrow interact only through a small degree of mixing with the standard model neutrinos. With such feeble interactions, such particles would have never been in thermal equilibrium in the early Universe, but instead would have been produced through the oscillations of the other neutrino species. Depending on their mass, such sterile neutrinos could be produced with a wide range of temperatures, and thus could constitute either a warm (mνs ∼ keV) or a cold (mνs ≫ keV) candidate for dark matter.
Among the particle species contained within the standard model, neutrinos are the only examples that are stable, electrically neutral, and not strongly interacting, and therefore are the only known particles that were viewed as potentially viable candidates for dark matter. Physicists' imagination, however, would not remain confined to the standard model for long, but instead would turn to the contemplation of many speculative and yet undiscovered candidates for the dark matter of our Universe. In particular, beginning in the early 1970s, many physicists began to consider the possibility that nature may contain a spacetime symmetry relating fermions to bosons, dubbed “supersymmetry” [133, 136, 186, 330]. Supersymmetry requires that for every fermion, a boson must exist with the same quantum numbers, and vice versa. Supersymmetry, therefore, predicts the existence of several new electrically neutral and non-strongly interacting particles, including the superpartners of the neutrinos, photon, Z boson, Higgs boson, and graviton. If any of these superpartners were stable, they could be cosmologically abundant, and may have played an important role in the history and evolution of our Universe.
The cosmological implications of supersymmetry began to be discussed as early as the late 1970s. In Piet Hut's 1977 paper on the cosmological constraints on the masses of neutrinos (as described above), the discussion was not entirely limited to neutrinos, or even to weakly interacting particles. Even the abstract of that paper mentions another possibility [164]:
Similar, but much more severe, restrictions follow for particles that interact only gravitationally. This seems of importance with respect to supersymmetric theories.
The paper goes on to close with the first cosmological bounds on the mass of the supersymmetric partner of the graviton, the spin 3/2 gravitino:
Assuming the standard big bang model to be relevant in the context of supergravity theories, one can make the following remark. If there exist light massive spin 3/2 particles interacting only gravitationally, having four spin degrees of freedom, their mass must be less than 15 eV if they are their own antiparticles, otherwise their mass is less than 1.5 eV. Also, they may exist with masses very much larger than 1 TeV.
Although such bounds would be revised in the decades to follow, in particular being shown to depend on the temperature to which the Universe was reheated following inflation, this result is essentially the basis of what is known today as the “cosmological gravitino problem”.
In their 1982 paper, Heinz Pagels and Joel Primack also considered the cosmological implications of gravitinos [23]. But unlike Hut's paper, or the other preceding papers that had discussed neutrinos as a cosmological relic, Pagels and Primack were clearly aware of the dark matter problem, and explicitly proposed that gravitinos could provide the solution by making up the missing mass [232]:
Gravitinos could also provide the dark matter required in galactic halos and small clusters of galaxies.
In many ways, Pagel and Primack's letter reads like a modern paper on supersymmetric dark matter, motivating supersymmetry by its various theoretical successes and attractive features, and going on to discuss not only the missing mass in galaxies and clusters, but also the role that dark matter could play in the formation of large scale structure. At the time of Pagel and Primack's submission, however, supersymmetry itself had not yet taken its modern form, and no truly realistic supersymmetric models had been proposed (although many important steps had been made in this direction [118, 119, 120, 121]). This changed in December of 1981, when a paper by Savas Dimopoulos and Howard Georgi described a model that would become known as the minimal supersymmetric standard model (MSSM) [93].
The advent of the MSSM opened the door to considering superpartners other than the gravitino as cosmological relics. In particular, in the MSSM, the superpartners of the photon, the Z, and two neutral scalar Higgs bosons mix to form four particles that would become known as neutralinos. Over the past three and a half decades, neutralinos have been the single most studied candidate for dark matter, having been discussed in many thousands of scientific publications. In order to be the dark matter, however, something must stabilize the lightest neutralino, preventing these particles from decaying shortly after being created.
In supersymmetric extensions of the standard model, there exist interactions that violate the conservation of baryon and lepton number. Unless the relevant couplings are highly suppressed, such interactions are expected to cause the proton to decay on unacceptably short timescales, on the order of a year or less. It was recognized early in supersymmetry's development, however, that the proton's lifetime could be made to safely exceed observational limits if an additional – and well-motivated – symmetry known as R-parity [118, 269, 121, 117] is imposed. The R-parity of a given particle is defined as follows:
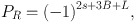 |
(1) |
where s is the spin of the particle, and B and L are the particle's baryon number and lepton number, respectively. Under this definition, all of the standard model particles have positive R-parity, PR = +1, while all of their superpartners have PR = −1. As a consequence, this parity ensures that superpartners can only be created or destroyed in pairs. A heavy superpartner can decay into a lighter superpartner, along with any number of standard model particles, but the lightest of the superpartners cannot decay. Thus if the lightest superpartner of the MSSM is either a neutralino or a sneutrino (the superpartner of a standard model neutrino), R-parity will stabilize it, allowing it to be a potentially viable dark matter candidate. As far as we are aware, it was Pagels and Primack who were the first to invoke R-parity in order to stabilize a dark matter candidate [232].
Papers discussing the cosmological implications of stable neutralinos began to appear in 1983 9. In the first two of these papers, Steven Weinberg [328] and Haim Goldberg [134] independently discussed the case of a photino – a neutralino whose composition is dominated by the superparter of the photon – and derived a lower bound of 1.8 GeV on its mass by requiring that the density of such particles does not overclose the Universe. A few months later, a longer paper by John Ellis, John Hagelin, Dimitri Nanopoulos, Keith Olive and Mark Srednicki considered a wider range of neutralinos as cosmological relics [113]. In Goldberg's paper, there is no mention of the phrase dark matter or of any missing mass problem, and Ellis et al. took a largely similar approach, simply requiring that the cosmological abundance of neutralinos not be so large as to overly slow or reverse the Universe's expansion rate. Ellis et al., however, did mention the possibility that neutralinos could make up the dark matter, although only in a single sentence [113]:
A more restrictive constraint follows from the plausible assumption that a non-relativistic [supersymmetric] fermion would participate in galaxy formation, in which case the limits on “dark matter” in galaxies allow one to deduce that ρχ ≤ 2 × 10−30 (Ω h2) gm/cm3.
and in a passing footnote of Ref. [114]:
This bound comes from the overall density of the universe and is very conservative. One can argue that massive neutral fermions probably condense into galaxies in which case a more stringent limit coming from missing galactic matter could be applied.
Although far from a full embrace of a particle physics solution to the dark matter problem, these sentences (along with those expressed by Pagels and Primack [232], and by Jim Peebles within the context of massive neutrinos [240]) reflected the emergence of a new perspective 10. Throughout the decades to follow, a countless number of particle physicists would motivate their proposals for physics beyond the standard model by showing that their theories could account for the Universe's dark matter. Despite any other attractive features that a given theory might possess, if it cannot provide a dark matter candidate, it would come to be viewed as incomplete.
That supersymmetric particles, and the lightest neutralino in particular, have received so much attention as dark matter candidates is due, in large part, to the fact that the motivation for supersymmetry does not primarily rely on the dark matter problem. Particle physicists have been drawn to supersymmetry over the past four decades for its ability to solve the electroweak hierarchy problem, and to enable gauge coupling unification [94, 165, 206], combined with its unique nature as both a spacetime symmetry and an internal symmetry [148]. If in some other universe, astrophysicists had measured the cosmological density of matter to be consistent with the observed density of stars, gas, and other baryons, particle physicists in that universe may have been just as interested in supersymmetry as they are in ours. In this respect, supersymmetry's ability to provide a viable dark matter candidate is seen by many particle physicists as something of a bonus, rather than as the primary motivation to study such theories.
Supersymmetry, however, is not the only particle physics framework that is both strongly motivated in its own right, and able to provide a viable candidate for the dark matter of our Universe. In the next section, we will turn our attention to perhaps the second most studied candidate for dark matter, the axion.
By all measures, quantum chromodynamics (QCD) has been an incredibly successful theory, and describes the strong force and the quarks and gluons which experience it with remarkable precision. That being said, QCD does suffer from one troubling issue, known as the strong-CP problem. This problem comes down to the fact that the QCD Lagrangian contains the following term:
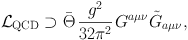 |
(2) |
where Ga µ ν is the gluon field strength tensor and Θ is a quantity closely related to the phase of the QCD vacuum. If Θ were of order unity, as would naively be expected, this term would introduce large charge-parity (CP) violating effects, causing the electric dipole moment of the neutron to be ∼ 1010 times larger than experimental upper bounds permit. Therefore, to be consistent with observations, the quantity Θ must be smaller than ∼ 10−10. While this could be nothing more than a highly unlikely coincidence, it has been interpreted by many as an indication that some new physics comes in to explain why Θ is so small. This is the essence of the strong-CP problem.
What is perhaps the most promising solution to this problem was proposed in 1977 by Roberto Peccei and Helen Quinn [234, 235]. They showed that by introducing a new global U(1) symmetry that is spontaneously broken, the quantity Θ can be dynamically driven toward zero, naturally explaining the small observed value. Later in the same year, Frank Wilczek [336] and Steven Weinberg [327] each independently pointed out that such a broken global symmetry also implies the existence of a Nambu-Goldstone boson, called the axion. The axion acquires a small mass as a result of the U(1) symmetry's chiral anomaly, on the order of ma ∼ λQCD2 / fPQ, where fPQ is the scale at which the symmetry is broken.
In its original conception, fPQ was taken to be near the weak scale, leading to an MeV-scale axion mass. This scenario was quickly ruled out, however, by a combination of laboratory and astrophysical constraints. In particular, in contradiction with observation, axions heavier than ∼10 keV are predicted to induce sizable rates for a number of exotic meson decays, such as K+ → π+ + a and J / ψ → γ + a. Similarly, axions heavier than ∼1 eV would lead to the very rapid cooling of red giant stars, again in contradiction with observations. Some years later, after the occurrence and observation of Supernova 1987A, even stronger constraints were placed on the axion mass, ma ≲ 10−3 eV.
In order to evade these constraints, axions must be much lighter, and much more feebly interacting [179, 286, 96], than had been originally envisioned by Wilczek and Weinberg. Such light and “invisible” axions, however, can have very interesting consequences for cosmology. Being stable over cosmological timescales, any such axions produced in the early Universe will survive and, if sufficiently plentiful, could constitute the dark matter.
A number of mechanisms have been considered for the production of axions in the early Universe. As with other particle species, axions can be produced thermally [313, 176]. For axions light enough to avoid the above mentioned constraints, however, the thermal relic abundance is predicted to be very small, and would only be able to account for a small fraction of the dark matter density. There is, however, another production mechanism, related to the misalignment of the Peccei-Quinn field, that is likely to be more important in the mass range of interest [95, 7, 249]. Although the quantity Θ is dynamically driven to zero by the mechanism proposed by Peccei and Quinn, its initial value was likely to be some much larger value, presumably determined through some random process. As the temperature of the Universe dropped below T ∼ λQCD, and the value of Θ was driven toward zero, the energy that had been stored in the Peccei-Quinn field gets transferred into the production of a non-thermal axion population. For typical initial conditions, this process of misalignment production is predicted to generate a density of axions that is comparable to the dark matter density for masses on the order of ma ∼ 10−5 eV. Alternatively, it was pointed out that as a consequence of Θ taking on different initial values in different locations throughout space, a network of topological defects (axionic strings and domain walls) may be expected to form. The subsequent decay of these defects is predicted to generate a quantity of axions that is comparable to that resulting from misalignment production [86]. Inflation will erase this network of topological defects, however, unless it occurs prior to the breaking of the Peccei-Quinn symmetry.
In light of these considerations, axions with masses in the range of ma ∼ 10−6 − 10−4 eV, and generated largely via misalignment production, have become one of the most popular and well-studied candidates for dark matter. Alternatively, it was also pointed out that if inflation occurs after the breaking of the Peccei-Quinn symmetry, then there may also be a viable anthropic scenario in which the axion mass could be much lighter [200, 337, 308]. In this scenario, the initial value of Θ is of order unity in most regions, leading to very high axion densities and to the rapid contraction of space.
In a small fraction of the overall cosmic volume, however, the initial value of Θ will be much lower, leading to far less axion production. If we speculate that life is only able to emerge in those regions in which the Universe is allowed to expand for millions or billions of years or more, we should expect to find ourselves in a region with a density of axions that is similar to the observed density of dark matter, even if the axion is much lighter than non-anthropic estimates would lead us to expect.
By the end of the 1980s, the conclusion that most of the mass in the Universe consists of cold and non-baryonic particles had become widely accepted, among many astrophysicists and particle physicists alike. And while alternatives continued to be discussed (see the following two chapters), cold dark matter in the form of some unknown species of elementary particle had become the leading paradigm. In addition to massive neutrinos (sterile or otherwise), supersymmetric particles (neutralinos, gravitinos, sneutrinos, axinos) and axions were each widely discussed as prospective dark matter candidates. And as the evidence in favor of non-baryonic dark matter became increasingly compelling, an ever greater number of particle physicists began to openly speculate about the nature of this invisible substance. The result of this was a long and diverse list of exotic possibilities, ranging from topological defects produced through spontaneous symmetry breaking in the early Universe (monopoles, cosmic strings) [177], to macroscopic configurations of quark matter (centimeter-scale “nuggets”, with nuclear-scale densities) [339], and even “pyrgons” (Kaluza-Klein excitations) that could appear within the context of models with extra spatial dimensions [185].
While this proliferation of dark matter candidates was taking place, however, a commonality among many of the proposed particles was becoming increasingly appreciated. In order for a particle species to freeze-out of thermal equilibrium in the early Universe to become a cold relic, it must not be too light (roughly heavier than ∼1-100 keV). Furthermore, for the predicted thermal relic abundance of such a species to match the observed dark matter density, the dark matter particles must self-annihilate with a cross section on the order of σ v ∼ 10−26 cm3/s (where v is the relative velocity between the annihilating particles). This number is strikingly similar to the cross section that arises from the weak force. For example, a stable neutrino with a mass of several GeV, annihilating through the exchange of a Z-boson, would freeze-out with a relic abundance that is roughly equal to the measured density of dark matter. Furthermore, such conclusions are not limited to neutrinos, but apply to a broad range of electroweak-scale dark matter candidates – including any number of stable particles with MeV-TeV masses and interactions that are mediated by the exchange of electroweak-scale particles.
This observation, combined with theoretical arguments in favor of the existence of new physics at or around the electroweak scale, have elevated weakly interacting massive particles (WIMPs) [305] to the leading class of candidates for dark matter 11. WIMPs have been the subject of thousands of theoretical studies, leading to the refinement of many calculations, including that of the dark matter's thermal relic abundance [300, 137, 143]. Furthermore, WIMPs (and to a somewhat lesser degree, axions) have motivated an expansive experimental program that continues to this day. With the advent of the Large Hadron Collider at CERN, and ever more sensitive astrophysical experiments, many believe that the moment of truth has come for WIMPs: either we will discover them soon, or we will begin to witness the decline of the WIMP paradigm [46].
5 Nicolas Bourbaki was a collective pseudonym adopted by a group of 20th-century mathematicians. Back.
6 As there existed no evidence for a third generation at the time, Gershtein and Zeldovich did not consider the tau neutrino. Back.
7 he terms “hot” and “cold” dark matter were coined in 1983 by Joel Primack and Dick Bond (J. Primack, private communication). Back.
8 A possible exception being the tau neutrino, whose mass would not be measured for another two decades, and thus could not at the time be ruled out as a cold dark matter candidate. Back.
9 Unstable but long-lived photinos had been considered earlier, in 1981, by Nicola Cabibbo, Glennys Farrar and Luciano Maiani [711] Back.
10 Early evidence for this transition can found in the conferences that took place over this period of time, including the “Study Week on Cosmology and Fundamental Physics”, that was held at the Vatican in September and October of 1981. Back.
11 Although the term WIMP, as coined by Gary Steigman and Michael Turner in 1984, was originally intended to include all particle dark matter candidates, including axions, gravitinos, etc., the definition of this term has since evolved to more often denote only those particles that interact through the weak force. Back.