


2.1. Evolution of the Energy Density in the Early Universe
The basic question addressed when investigating the history of the Universe as a whole in the framework of modern physics is the following: Why do we see something instead of detecting nothing? It originates from the common wisdom that any isolated system after long enough evolution will reach thermal equilibrium, characterized by a homogeneous structureless distribution of its energy. Nearly 14 billion years after the Big Bang, one observes the presence of complicated hierarchical structures on all scales, starting from the subnuclear world, through chemical elements, and up to the scale of galaxy clusters. This section will review our present understanding of how the structured evolution of the Universe could be sustained for a time more than 60 orders of magnitude longer than the characteristic timescale of the particle physics processes present at the moment of its 'birth.'
The information concerning the constitution of the early Universe has increased tremendously during the past decade, mainly due to improved observations of the cosmic microwave background radiation (CMBR). The most important cosmological parameters (the total energy density, the part contained in baryonic matter, the part of nonbaryonic dark matter (DM), other components, etc.) have been determined with percent level accuracy as a result of projects completed in the first decade of the twenty-first century and now appear in tables of fundamental physical data (Amsler et al. 2008).
The existence of CMBR was predicted by Alpher et al. (1948) as a direct consequence of the Hot Big Bang Universe of Gamow (Lamarre and Puget 2001). It was discovered by Penzias and Wilson (1965). It originates from the combination of the once free electrons and protons into neutral atoms when the temperature of the Universe dropped below kT = 13.6 eV (the ionization energy of the H-atom, i.e., T = 1.58 × 105 K) to nearly 1 eV (1.16 × 104 K). (Note that in certain branches of physics it is customary to express temperature in eV units through the equation E = kT. The conversion is given by 1 eV corresponds to 1.16045 × 104 K.) After the recombination, the Universe became transparent to this radiation, which at present reaches the detectors with a redshift determined by the kinematics of the expansion of the Universe (Lamarre and Puget 2001). It appears to be a perfect thermal radiation with Planckian power distribution over more than three decimal orders of magnitude of frequency, having a temperature of T = 2.725 ± 0.001 K.
The first quantitative evidence for the temperature anisotropy of CMBR was provided by the COBE (Cosmic Background Explorer) satellite in 1992. The angular resolution of its detectors was 7°. This enabled the collaboration to determine the first 20 multipole moments of the fluctuating part of CMBR beyond its isotropic component. It has been established that the degree of anisotropy of CMBR is one part in one hundred thousand (10−5). There are two questions of extreme importance related to this anisotropy:
Section 2.4 returns to the answer to the first question. To the second question, the answer will be briefly outlined below.
Following the success of the COBE mission several more refined (ground based and balloon) measurements of the CMBR fluctuations were performed between 1998 and 2001. An angular resolution of about 1° has been achieved, which was further refined to the arc-minute level by the satellite mission Wilkinson Microwave Anisotropy Probe (WMAP). The combined efforts of these investigations allowed the determination of the multipole projection of CMBR on the sky up to angular moments l = 2,000. The fluctuation information extracted until 2007 is presented in Fig. 1 with lmax = 2,000. One easily recognizes the presence of three pronounced maxima in this figure (possible additional, weaker maxima are discussed further below).
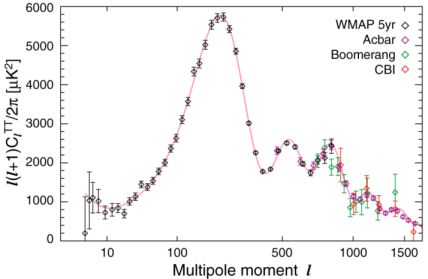 |
Figure 1. Multipole fluctuation strength of the cosmic microwave background radiation as a function of the spherical harmonic index l. The location and the height of the first minimum favors a spatially flat Universe, while the level of the fluctuations in the higher multipoles (l > 400) indicates the presence of a low-density baryonic component (< 5%). The measurements cover already the damping region (l > 1,000). Wilkinson Microwave Anisotropy Probe (WMAP) data are displayed together with results of earlier balloon observations (Reprinted from Nolta et al. 2009 with kind permission of the first author, the WMAP Science Team, and AAS) |
Another important characteristic of the CMBR anisotropy is its spectral power distribution. The measured distribution is nearly scale invariant; it is the so-called Zel'dovich–Harrison spectrum (see Peebles 1993). This means that every unit in the logarithm of the wave number contributes almost equally to the total power.
The small-amplitude and almost scale-invariant nature of the fluctuation spectra, described above, reflects the very early fluctuations of the gravitational field. First of all, one has to emphasize that the coupled electron–proton–photon plasma near recombination was oscillating in a varying gravitational field (Hu 2001). Where the energy density was higher the plasma experienced the effect of a potential well, and the radiation emerging from this region was hotter than average. On the contrary, diminutions of the energy density led to a colder emission. Still, an observer located far from the sources detects lower temperature from denser sources due to the Sachs–Wolfe effect (Peebles 1993). In any case, the CMBR anisotropy actually traces the inhomogeneity of the gravitational potential (or total energy density) in the era of recombination.
Thomson scattering of the anisotropic CMBR on the ionized hot matter of galaxy clusters and galaxies results in roughly 5% linear polarization of CMBR. Its presence in CMBR was first detected by the Degree Angular Scale Interferometer (DASI) experiment (Kovac et al. 2002). Starting from 2003, the WMAP experiment also measured the temperature–polarization cross correlation jointly with the temperature–temperature correlation. The significance of this type of measurement is obvious since the presence of ionized gases corresponds to the beginning of the epoch of star formation.
Inflationary Interpretation of the CMBR
A unique particle physics framework has been proposed, which can account
for the energy density fluctuations with the characteristics found in
CMBR. One conjectures that the large-scale homogeneity of the Universe
is due to a very early period of exponential inflation in its scale
(Peebles 1993).
One assumes that during the first era after the Big Bang the size of the
causally connected regions (the horizon) remained constant, while the
global scale of the Universe increased exponentially. This is called
inflationary epoch. The wavelength of any physical object is redshifted
in proportion with the global scale. Therefore, at a certain moment,
fluctuations with a wavelength bigger than the horizon were "felt" as
constant fields and did not influence anymore the gravitational
evolution of the matter and radiation at smaller length scale.
The inflationary period in the evolution of the Universe ended at about
10−32 s after the Big Bang. At this moment, the
constant ordered potential energy density driving the inflation decayed
into the particles observed today. Some of them may have belonged to a
more exotic class, which can contribute to the violation of the
matter–antimatter symmetry if they exhibit sufficiently long
lifetimes (see Sect. 2.2). The rate of expansion of
the horizon in the subsequent radiation- and matter-dominated eras was
always faster than the global expansion of the Universe (see
Fig. 2). Radiation-dominated means that the main
contribution to the energy density comes from massless and nearly
massless particles with much lower rest energy than the actual average
kinetic energy. Therefore, the long-wavelength fluctuations having left
during inflation continuously reentered the horizon and their
gravitational action was "felt" again by the plasma oscillations. The
first maximum of the CMBR multipole moments corresponds to the largest
wavelength fluctuations that were just entering the horizon in the
moment of the emission of CMBR.
Since during its evolution beyond the horizon, any dynamical change in
the fluctuation spectra was causally forbidden, the fluctuating
gravitational field experienced by the recombining hydrogen atoms was
directly related to the fluctuation spectra of the inflationary epoch,
determined by the quantum fluctuations of the field(s) of that era. This
observation leads promptly to the conclusion that the spectra should be
very close to the Zel'dovich–Harrison spectra. Detailed features
of the power spectra seem to effectively rule out some of the concurrent
inflationary models.
Also the simplest version of the field-theoretical realization of
inflation predicts a total energy density very close to the critical
density ρc, which separates the parameter region of a
recollapsing Universe from the region where a non-accelerating expansion
continues forever. Such a Universe is spatially flat. In the apparently
relevant case of accelerated expansion, the borderline is shifted and
universes somewhat above the critical densities might expand with no
return. It is customary to measure the density of a specific constituent
of the Universe in proportion to the critical density:
Ωi = ρi / ρc.
An important prediction of the inflationary scenario for the origin of
CMBR anisotropy is a sequence of maxima in the multipole spectrum
(Hu 2001).
The latest results (see Fig. 1) confirm the
existence of at least two further maxima, in addition to the main
maximum known before. The new satellite-based CMBR observations by the
European satellite PLANCK launched in May 2009 will improve the accuracy
of the deduced cosmological parameters to 0.5% and determine the
multipole projection of the anisotropy up to angular momentum l
∼ 2,500.
The positions and the relative heights of these maxima allow the
determination of the relative density of baryonic constituents among the
energy carriers. The increased level of accuracy leads to the conclusion
that the baryonic matter (building up also the nuclei of all chemical
elements) constitutes no more than 5% of the energy content of the
Universe. This conclusion agrees very convincingly with the results of
the investigation of the primordial abundance of the light chemical
elements to be described in detail in
Sect. 3. These facts lead us to the
unavoidable conclusion that about 95% of the energy content of the
Universe is carried by some sort of nonbaryonic matter. (More accurate
numbers will be given at the end of this section). The discovery of its
constituents and the exploration of its extremely weak interaction with
ordinary matter is one of the greatest challenges for the scientific
research in the twenty-first century.
Dark Matter: Indications, Candidates, and Signals
Beyond CMBR, growing evidence is gathered on a very wide scale for the
existence of an unknown massive constituent of galaxies and galaxy
clusters. It is tempting to follow a unified approach describing the
"missing gravitating mass" from the galactic to cosmological scale
(i.e., from a few tens of kpc to Mpc, with 1 pc = 3.26 light-years =
3.0856 × 1013 km). In this subsection the main
evidence already found and the ongoing experimental particle physics
efforts for direct detection of the dark matter (DM) constituents are
shortly reviewed.
First hints of some sort of gravitating Dark Matter below the
cosmological scale came from galactic rotation curves (some tens of
kpc), then from gravitational lensing (up to 200 kpc), and from the
existence of hot gas in galaxy clusters. The anomalous flattening of the
rotation curves of galaxies was discovered in the 1970s. Following
Kepler's law, one expects a decrease of the orbiting velocity of all
objects (stars as well as gas particles) with increasing distance from
the galactic center. Instead, without exception a tendency for
saturation in the velocity of bright objects in all studied galaxies is
observed. The simplest explanation is the existence of an enormous dark
matter halo. Since velocity measurements are based on the 21 cm hydrogen
hyperfine radiation, they cannot trace the galactic gravitational
potential farther than a few tens of kiloparsecs. Therefore, with this
technique only the rise of the galactic dark matter (DM) haloes can be
detected but one cannot find their extension.
Dark supermassive objects of galactic cluster size are observable by the
lensing effect exerted on the light of farther objects located along
their line of sight. According to general relativity the light of
distant bright objects (galaxies, quasars,gamma ray bursts(GRBs))
will be bent by massive matter located between the light source and the
observer along the line of sight. Multiple and/or distorted images
arise, which allow an estimate of the lensing mass. The magnitude of
this effect, as measured in the Milky Way, requires even more DM out to
larger distances than it was called for by the rotation curves
(Adelmann-McCarthy
et al. 2006).
The large-scale geometry of the galactic DM profile semiquantitatively
agrees with results of Newtonian many-body simulations, though there are
definite discrepancies between the simulated and observed gravitating
densities at shorter distances. Interesting propositions were put
forward by Milgrom to cure the shorter-scale deviations with a modified
Newtonian dynamics (MOND) (reviewed by
Milgrom 2008).
Gravitational lensing combined with X-ray astronomy can trace the
separation of bright and dark matter, occurring when two smaller
galaxies collide. The motion of the radiating matter is slowed down more
than that of the DM components. As a consequence, the centers of the
lensing and X-ray images are shifted relative to each other. A recent
picture taken by the Chandra X-ray Telescope is considered as the first
direct evidence for the existence of DM on the scale of galaxy clusters
(Clowe et
al. 2006).
Another way to estimate the strength of the gravitational potential in
the bulk of large galaxy clusters is offered by measuring
spectroscopically the average kinetic energy (e.g., the temperature) of
the gas. One can relate the very high temperature values (about
108 K) to the depth of the gravitational potential assuming
the validity of the virial theorem for the motion of the intergalactic
gas particles. Without the DM contribution to the binding potential the
hot gas would have evaporated long ago.
Three most popular DM candidates could contribute to the explanation of
the above wealth of observations. Historically, faint stars/planetary
objects constituted of baryonic matter were invoked first, with masses
smaller than 0.1 solar mass (this is the mass limit minimally needed for
nuclear burning and the subsequent electromagnetic radiation). The
search for massive compact halo objects (MACHOs) was initiated in the
early 1990s based on the so-called microlensing effect – a
temporary variation of the brightness of a star when a MACHO crosses the
line of sight between the star and the observer. This effect is
sensitive to all kind of dark matter, baryonic or nonbaryonic. The very
conservative combined conclusion from these observations and some
theoretical considerations is that at most 20% of the galactic halo can
be made up of stellar remnants
(Alcock et
al. 2000).
Complementary to this astronomy-based proposition elementary particle
physics suggests two distinct nonbaryonic "species", which originate
from the extreme hot period of the Universe and therefore could be
present nearly homogeneously on all scales. Axions are
hypothetical particles of small (10–(3–6)
eV/c2) rest energy. They were introduced
(Peccei and Quinn
1977)
for the theoretical explanation of the strict validity of the symmetry
of strong interactions (QCD) under the combined application of space-
and charge reflections (CP-invariance). Although they are very light,
their kinetic energy is negligible, since they are produced in
nonthermal processes. This way they represent the class of cold dark
matter. The parameter space was and is thoroughly searched for axions in
all particle physics experiments of the last 2 decades. The presently
allowed mass range is close to the limit of the astrophysical
significance of these particles.
The most natural DM candidates from particle physics are weakly
interacting massive particles (WIMPs). Assuming that the thermal
abundance of the WIMPs is determined by the annihilation and
pair-production processes with themselves, one can estimate their
present density as a function of the annihilation cross section. It is
quite remarkable (even qualified sometimes as "WIMP
miracle") that, using cross sections typical of the
supersymmetric extension of the standard particle physics model, just
the gravitating density missing on the cosmological scale is found. By
this coincidence, one identifies WIMPs with the lightest stable
supersymmetric particle (called neutralino). The neutralino's mass is on
the scale of heavy nuclei; usually one assumes it to equal the mass of
the tungsten atom. It would constitute pressureless cold dark matter,
with a density calculable by analyzing its decoupling from thermal
equilibrium.
An important milestone in the WIMP-story will be reached once the Large
Hadron Collider (LHC) at CERN begins working. The available energy
covers the expected mass range of the most popular variants of
supersymmetric extensions. Currently, extensive strategies are worked
out for the identification of prospective new massive particles to be
observed at LHC, along with their cosmologically motivated counterparts
(Baltz et
al. 2006).
A positive identification at CERN would give new impetus to the
underground direct searches for WIMPs. Such research is based on looking
for heat deposition by particles arriving from the nearest galactic
neighborhood into cryogenic detectors, well isolated from any other type
of heat exchange. At present, only a single such experiment, i.e., the
Dark Matter (DAMA) experiment in Gran Sasso, Italy, has reported a
positive signal in the DM particle search. For more than 5 years now, a
seasonal variation in the heat deposition rate is observed, which may be
caused by the DM particle flux variation along the orbit of the Earth
(Bernabei et
al. 2003).
Although the analysis of CMBR excludes the domination of hot dark
matter, i.e., relativistic weakly interacting particles, like light
neutrinos, there still exists a plethora of more exotic propositions for
the constituents of dark matter, not yet accessible for experimental
verification, like primordial black holes, nonthermal WIMPzillas, and
the so-called Kaluza–Klein excitations of higher-dimensional
theories.
Dark Energy, the Accelerating Universe, and the
Problem of Distance Measurements
The expansion of the Universe is conventionally characterized by the
Hubble law, stating that cosmological objects uniformly recede from the
observer with a velocity proportional to their distance. The
proportionality factor H has not remained constant during the
evolution of the Universe, the rate of change being characterized by the
deceleration parameter q0 =
dH–1 / dt – 1
(Peebles 1993).
The deceleration can be probed by distance measurements using type Ia
supernovae. As explained in Sect. 5.3
these very energetic cosmic events occur in a rather narrow mass range
of compact objects, with a minimal scatter in their energy output or
luminosity L, which determines also the energy flux F
reaching the observer at distance dL called
luminosity distance. Therefore, type Ia supernovae are standardizable
light sources (standard candles), their light curves can be transformed
into a universal form.
Standard candles are important tools to measure astronomical
distances. Knowing the luminosity (i.e., energy output) of an object, it
is straightforward to calculate its distance by the observed brightness,
which drops with the inverse square of the distance 1 /
r2. The advantage of using SN Ia is that they are
outshining all the stars in a regular galaxy and thus can be seen and
studied over vast distances.
More recently, the method of measuring distances with SN Ia has acquired
some fame by showing that the Universe is expanding faster at large
distances than expected by the standard cosmological model
(Perlmutter et
al. 1999;
Riess et al. 1998;
Leibundgut 2001a,
b).
The luminosities of 42 SN Ia were analyzed in these pioneering
publications as a function of their
redshift. The survey comprised objects
with redshift z ≤ 1, which corresponds to an age
≤ 10 Ga (gigayears). Assuming that the absolute magnitude of these
objects is independent of the distance (excluding evolution effects) the
apparent luminosities were detected on an average 60% fainter than
expected in a Universe, whose energy density is dominated by
nonrelativistic matter. A number of data points with z ≤
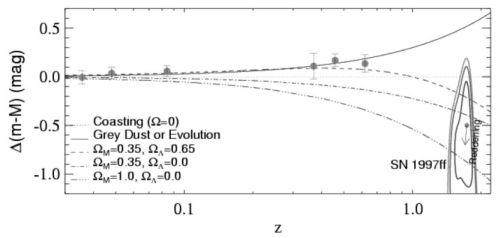
0.7 are displayed in Fig. 3, all having positive
deviation for the
difference of the apparent and absolute luminosities,
m – M (note that the fainter is a source the larger is
its magnitude). The simplest interpretation is to assume the scattering
of the light on its way from the source by some sort of
"dust" (full line) leading to objects that are fainter
than foreseen. A less conventional interpretation is to assume positive
acceleration of the global expansion. (An accelerating source is located
farther away, and will appear to be fainter at a certain z than
expected in standard cosmology.)
Figure 3. Variation of the difference of
the observed (m) and absolute (M) luminosity for the
SN Ia with redshift z, measured in a special astronomical
unit, called magnitude. The zero level corresponds to
supernovae in an empty (Ω = 0) Universe. A positive
difference signals sources that are fainter than expected. A brighter
(negative) value is naturally interpreted as the decelerating action of
the gravitational force exerted on the source by a nonzero rest energy
(ΩM ≠ 0). See text for models corresponding to the
different curves possibly producing positive values (Reprinted from
Riess et al. 2001
with kind permission of the first author and AAS)
The quantitative argument is based on relating the measurements to the
deceleration parameter defined above. In fact the luminosity distance of
an object at redshift z can be expressed as an integral of an
expression of the varying Hubble-parameter H(z) on the
interval (0, z), where z = 0 corresponds to the
observer's position today. When the redshift is not too large, one can
expand this integral into a series of z and arrive in the first
approximation at a simple linear relation expressing Hubble's law of the
dependence of the luminosity distance on the redshift. Its first
nonlinear correction involves the deceleration parameter:
dL = (c / H0) z [1 +
(1 - q0) z / 2 + ...]. Dust absorption
diminishes the source brightness irrespective of the value of
z. On the other hand, the presence of both matter and a
cosmological constant will change the sign of the deceleration parameter
with z.
In the past decade several projects contributed to the luminosity
distance measurements and by now (i.e., as of 2009) the list includes
over 200 events. Specifically with the help of the Hubble telescope 13
new Sn Ia were found with spectroscopically confirmed redshifts
exceeding z = 1 and at present the full sample contains already
23 z > 1 objects
(Riess et
al. 2007).
Such objects most strongly influence the value of the deceleration
parameter. A combined analysis of all Sn Ia data yields a deceleration
parameter value of -0.7 ± 0.1
(Kowalski et
al. 2008).
Its negative value signals an accelerating expansion rate at distance
scales comparable to the size of the Universe.
A nonzero cosmological constant Λ in the equations describing the
dynamics of the Universe can account for such an acceleration. The
cosmological constant is related to a vacuum energy
density (ρ) characterized by negative pressure (equation of state
p = w ρ, with w = -1). Nowadays, the
more general term 'dark energy' is used for the
hypothetical agent of such an accelerating
effect (acceleration requires w < -1/3).
The fraction of the total energy density stored in Λ is
not constant in time. Although Λ is constant by
definition, the energy densities in the radiation and matter components
are varying respectively as quartic and cubic inverse powers of the
distance scale of the Universe. The early Universe until the decoupling
of the photons is radiation-dominated and the Λ energy
density is negligible. Initially, the matter density (including
nonbaryonic dark matter) is dominating after decoupling, exerting a
conventional decelerating effect on the motion of cosmological
objects. Because of the reduction of the matter density with the
expansion of the Universe, its contribution to the total energy density
(and total Ω = ΩM + ΩΛ)
may become smaller than the one of Λ at a given point in
time. How early this crossover happens depends on the absolute value of
Λ, which is not constrained by any current theory. From
this point of view, it is remarkable that ΩM and
ΩΛ are of the same order of magnitude in the
Universe at present. Because of this and the rather small value of
Λ its impact on the cosmic expansion can only be
detected over large distances, i.e., when studying distances of objects
with large redshift z. In the distant future, the repulsive
action of a nonzero Λ will more and more
dominate. Without any additional effect, this leads to a 'Big
Rip' scenario in which smaller and smaller volumes become
causally isolated because the repulsion will be pushing everything apart
faster than the speed of light.
The different fits in Fig. 3
correspond to different matter – dark energy
compositions. Without cosmological constant, the deviation is always
negative but its rate of decrease depends on ΩM. The
two lower curves show cases (ΩM = 0.35 and 1.00,
respectively), which do not fit the measurements at all. Evidently, if
the measurements are correct, some sort of dust or dark energy will be
needed.
Because of the important consequences of these observations on
cosmology, astronomers seriously investigate possible alternatives or
data biases, such as possible effects of the evolution of SN Ia objects
(deviation from the 'standard candle' behavior at low metallicity),
effects of light absorption by the galaxy clusters hosting the
supernovae, and by the intergalactic dust, lensing effects,
etc. Although the actual dust content in the line of sight is not well
determined, dust is not a problem in recent observations because
astronomers make use of an empirical relation between the width of the
SN Ia lightcurve (between rise and decay) and its absolute magnitude. By
studying samples of closer SN Ia it was found that more energetic,
brighter explosions also lead to a wider lightcurve. This is called the
Phillips relation. It is not affected by dust absorption and the only
assumption entering is that it is universally valid for all SN Ia. Thus,
knowing the easily determinable lightcurve width, the absolute magnitude
can be derived and the distance calculated by comparison to the observed
relative magnitude of the explosion.
The best fit rather indicates the presence of dark energy. This
conclusion was largely determined by the object with largest z
observed to date. In 2001, a SN Ia with z = 1.6 was reported
with larger apparent luminosity than expected in a matter dominated or
in an empty Universe
(Riess et
al. 2001<>,
see 3). It can be reconciled with the small
z observations by assuming that it exploded in an epoch when
the matter part of the energy density was still dominant and the rate of
the expansion was decreasing. Quantitatively, the fit led to
ΩM = 0.35, ΩΛ = 0.65.
The important question to be addressed in this context is the one
regarding alternatives concerning the nature of the repulsive force. A
cosmological constant implies an equation-of-state with w = -1
but any w < -1/3 yields repulsion. An additional, previously
unknown, form of energy has been postulated as an alternative to the
cosmological constant: Quintessence
(Caldwell et
al. 1998;
Armendariz-Picon et
al. 2000).
It has repulsive properties but w ≠ -1. Therefore, it can be
time-dependent and even have different values at different spatial
points, contrary to a cosmological constant. Detailed SN Ia
investigations try to put bounds not just on the size of the
acceleration but also on the type of dark energy, i.e., the
equation-of-state of the Universe.
The most recent analyses
(Riess et
al. 2007;
Wood-Vasey et
al. 2007)
employing much larger data sets than before are all compatible with the
cosmological constant (w = -1) interpretation of the data and
give ΩM = 0.274 with 20% statistical error. A final
conclusion concerning the acceleration driven by a substantial
cosmological constant might be reached by the proposed Supernova
Acceleration Probe space mission. The project aims at the observation of
around 2,000 SN Ia up to a redshift z ≤ 1.2. Its launch
is tentatively scheduled for 2013.
The results of 5 years of WMAP satellite mission were published and
their cosmological interpretation was studied
(Komatsu et
al. 2009),
taking into account the
effect of the above-listed investigations. The results were interpreted
by assuming that our Universe is flat and its energy content is a
mixture of ordinary matter, gravitating dark matter, and dark
energy. The most important cosmological parameters were determined with
unprecedented accuracy. The accuracy was substantially increased by
combining the WMAP CMBR data, type Ia supernova luminosity distance
measurements, and the largest scale components of the 2dF galaxy cluster
catalogue
(Percival et
al. 2007).
The supernova data are
sensitive to the energy density component of cosmological constant type,
while the galaxy clusters represent the aggregates of the gravitating
(mainly dark) matter. The analysis results in a value of the Hubble
parameter H at present time of (70.1 ± 1.3) km
s-1 Mpc-1. The ordinary matter content is (4.62
± 0.15)%, the cold (nonrelativistic) dark matter represents (23.3
± 1.3)%, the part of the dark energy in the full energy density
is 72.1 ± 1.5%. The projection of the motion of such a Universe
back in time leads to a highly accurate estimate of its age: 13.73
± 0.12 billion years.
Concluding, it becomes a more and more established fact that the
chemical elements formed from baryonic matter contribute less than 5% to
the total energy density of the present Universe. In view of the
complete symmetry of laws governing matter and antimatter in our
present-day Universe it is actually a rather nontrivial fact that
baryonic matter did not completely annihilate into radiation in the hot
Universe directly after the inflationary epoch and also that the
original energy density was transformed into a high-temperature gas of
ordinary elementary particles.
2.2. Origin of the Matter–Antimatter
Asymmetry
On the interface of neighboring domains of baryonic and antibaryonic
matter, quark–antiquark (proton–antiproton) annihilation
would lead to the emission of hard X-rays. The absence of this signal
makes it highly probable that even if antibaryons were present in the
early, hot Universe they had disappeared before the CMBR was
emitted. Therefore, the observed baryonic density actually proves the
presence of a matter–antimatter asymmetry within the present
horizon in our Universe
(Rubakov and
Shaposhnikov 1996;
Riotto and Trodden
1999).
In 1967, Sakharov analyzed the conditions that might lead to this
asymmetry dynamically, instead of simply assuming it to be fixed by some
initial conditions
(Sakharov 1967).
If, in a certain moment,
The elementary interactions violate the symmetry under the combined
transformation consisting of spatial reflection (P) followed by charge
conjugation (C) – the so-called CP symmetry,
The elementary interactions violate the baryon-antibaryon symmetry,
The Universe is out of thermal equilibrium,
then a matter–antimatter density difference is produced. One can
deduce the actual amount of asymmetry with detailed quantitative
calculations.
Without going into details, some of the scenarios proposed by
theoretical particle physicists for the creation process of this
fundamental asymmetry will be outlined below. For this, a short account
of the Standard Model of elementary interactions
(Perkins 2000)
is given first. (See also Chap. 10, Vol. 1)
Known elementary constituents of matter are quarks and leptons
(see Table 1). Three families have been
discovered. In each family one has two flavors of quarks and one lepton
with the associated neutrino. The decay of the free neutron observed in
1932 and described first by the Fermi theory of weak interactions is
understood today as the decay of a d-quark (one of three quarks
composing the neutron) into a u-quark (which forms the final proton with
the unchanged other two quarks) and an electron plus its
antineutrino. The particles participating in this process constitute the
lightest (first) particle family of the Standard Model.
Three elementary interactions act among these particles. Each of them is
mediated by vector particles. The electromagnetic quanta, the photons,
bind nuclei and electrons into atoms and molecules. Weak interactions
are mediated by three vector fields, the W± and the
Z0, all discovered in 1983. Gluon fields bind the quarks
into protons and neutrons. The strong interaction quanta come in eight
different, so-called colored states and also each quark can appear in
one of three different colored states.
It has been shown that the three Sakharov conditions might be fulfilled
simultaneously in the Standard Model at high temperatures. The
CP-violation, which allows the oscillation of the K0 and of
the B0 mesons into their antiparticles and back, has been
observed experimentally (in 1967 and 2001, respectively) and can be
quantitatively understood with the present theory
(Amsler et
al. 2008).
On the other hand, no sign of baryon number violation has been observed
to date in any elementary particle physics experiment. In the Standard
Model, one cannot find any process that would involve the transformation
of a proton into mesons or leptons. However, in the early 1970s,
't Hooft (1976)
showed that in the presence of specific configurations of electro-weak
vector fields, fermions (leptons and quarks) can be created or
annihilated, but the difference of the baryon number and of lepton
number (B - L) should stay constant (quarks and
antiquarks actually carry ±1/3 unit of baryon charge, while the
lepton charge of the known species is ±1). Today the chance for
such transitions to occur is negligible (the probability is estimated to
about 10-170). However, they must have occurred frequently
when the temperature was of the order of 100 GeV (about 1015
K).
It is a very interesting coincidence that exactly at that temperature
scale one expects the transformation of all elementary particles from
massless quanta into the massive objects observed in today's
experiments. The creation of the mass is due to the so-called Higgs
effect. This consists of the condensation of an elementary scalar field
(a close relativistic analogue of the Cooper-pairing in
superconductivity). If this transformation had proceeded via a
sufficiently strong first-order phase transition, the third of
Sakharov's criteria had been also fulfilled by the behavior of the known
elementary interactions in the very early Universe.
In a first-order phase transition, the low-temperature (massive) phase
would appear via thermal nucleation, which is a truly
far-from-equilibrium process. Inside the bubbles of the new phase the
baryon number-violating processes are stopped. So the question is this:
What is the net baryon concentration frozen?
Quarks and antiquarks traverse the phase boundaries, which represent a
potential barrier for them. As a consequence of the complex CP-violating
phase in the Hamiltonian describing weak interactions, the reflection
and transmission amplitudes for matter and antimatter turn out to be
different leading to an asymmetry in the constitution of matter and
antimatter inside the bubbles.
The quantitative details of this beautiful scenario critically depend on
a single parameter: the strength of the self-coupling of the so-called
Higgs field, whose condensation determines the masses of all
particles. This parameter is still unknown. The latest lower bound
(Amsler et al. 2008)
lies in a region where the phase transformation is actually continuous
(beyond the end point of the first-order transition line). The situation
could be different in supersymmetric extensions of the Standard
Model. The one explored best is the electroweak phase transition within
the so-called Minimal Supersymmetric Standard Model
(Carena et
al. 2009).
One expects considerable guidance from measurements at the Large Hadron
Collider in constraining the parameter space to search for the origin of
baryon–antibaryon asymmetry. Another avenue could be the very
late (low-energy density) exit from the inflationary period of evolution
(Garcia-Bellido et
al. 1999;
Krauss and Trodden
1999;
van Tent et
al. 2004).
If this energy scale coincides with the electroweak mass scale then the
reheating of the Universe from its cold inflationary state would offer
an out-of-equilibrium situation. This is the basis of the proposition of
the cold baryogenesis scenario
(Tranberg et
al. 2007).
The resolution of the matter–antimatter asymmetry problem is an
issue of central importance in particle physics in the twenty-first
century.
2.3. Evolution of the Expanding Universe
The equilibrium in the hot particle "soup" is
maintained through frequent elementary particle reactions mediated by
the quanta of the three fundamental interactions. The expansion of the
Universe dilutes the densities and, consequently, the reaction rates get
gradually lower. The adiabatic expansion lowers monotonically also the
temperature (the average energy density). (Actually, there is a
one-to-one mapping between time and temperature.) The following
milestones can be listed in the thermal history of the Universe
(Kolb and Turner
1990).
First, the weak interaction quanta became massive at the temperature
scale of 100 GeV. Since then, weak reactions have only occurred in
contact interactions of the particles. At about the same time the
t-quark and the Higgs quanta also decoupled from the 'soup'. The same
decoupling happened for the other heavy quark species (b-quark, c-quark)
and for the heaviest of the leptons (τ-particle) in the range
1–5 GeV (a few times 1013 K) of the average energy
density. The τ-neutrinos remain in thermal equilibrium via weak
neutral interactions.
The strong interaction quanta, the gluons became extremely short ranged
at around the temperature kT ∼ 100–200 MeV (a few
times 1012 K). Computer-aided quantum field theoretical
investigations have demonstrated that quarks and gluons are confined to
the interior of nucleons (protons and neutrons) and excited baryonic
resonances below this temperature range
(Petreczky 2007).
This transformation was smooth for baryonic matter densities
characteristic of our Universe at that epoch and for the actual mass
values of the light quarks, very similar to the process of atomic
recombination.
At this stage no nuclear composite objects can be formed yet, since they
would instantly disintegrate in collisions with hard electromagnetic
quanta. The stabilization occurs for temperatures below 0.1
MeV. Primordial synthesis of light nuclei took place at that cooling
stage of the Universe (Sect. 3).
Below this temperature, light nuclei and electrons form a globally
neutral plasma, in which thermal equilibrium is maintained exclusively
by electromagnetic interactions. The gravitational attraction of the
massive and electrically screened constituents of matter was balanced by
the radiation pressure. This dynamical equilibrium is described by
coupled fluid equations and results in acoustic oscillations modulating
the essentially homogeneous distribution of the constituents
(Hu 2001).
The dominant wavelength of these oscillations is determined by those
density fluctuation modes that left the horizon during inflation and are
continuously reentering, since during the radiation-dominated period,
the horizon expands faster than the global scale parameter of the
Universe increases.
The last qualitative change occurred at the energy scale around 1 eV
(∼104 K), when at the end of atomic recombinations the
Universe became transparent to the propagation of electromagnetic
radiation. At this moment the size of the Universe was about 1/1000 of
its present radial scale. Today, the light emitted in the act of the
last scattering is detected as cosmic microwave background radiation. A
consistent interpretation of the details of its features represents
(together with the primordial abundance of light nuclei) a unique test
of all ideas concerning the earlier evolution of the Universe.
2.4. Gravitational Clustering of Matter
At the moment of the decoupling of light, the matter in the Universe
became gravitationally unstable against density fluctuations. The key
feature in understanding the emergence of a large-scale structure in the
Universe is the statistical characterization of the density fluctuations
at this moment. These fluctuations are determined by the spectra of the
acoustic oscillations, which are in turn determined by the reentering
density fluctuations of inflationary origin. This line of thought leads
us to the hypothesis of the quantum origin of the largest-scale
structures observed in the Universe.
Amplitudes of density fluctuations at different wavelengths follow
independent Gaussian (also called normal)
statistics (see Sect. 3.6, Chap. 9, Vol. 1), and their mean spectral
power is distributed in an almost scale-invariant manner, described
above. The absolute normalization was determined by the COBE satellite
to be 1 part in 100,000. Their evolution can be analyzed initially with
the help of the linearized gravitational equations. The classical
analysis, originally performed by
Jeans (1902),
leads to the conclusion that fluctuations above the Jeans-scale are
unstable and they are at the origin of the formation of the oldest
structures (for a modern textbook on the subject, see
Peacock 1999).
The nonlinear stage of the clustering process can only be followed by
numerical integration of Newton's equations of motion for a very large
number (typically 106–107) of equal-mass
particles. The most interesting question studied in these
N-body simulations concerns the mass distribution of the first
galaxies. This feature determines the frequency of the occurrence of
densities sufficiently high to start nuclear fusion reactions in these
first gravitationally bound galactic objects.
The semiempirical theory
(Press and
Schechter 1974)
assumes that this distribution is determined by the probability of
matter fluctuations obeying a Gaussian distribution to exceed an
empirically determined threshold value. This simple idea results in an
∼M-2/3 power scaling for the statistics of the
collapsed objects with different mass M. This means that the
earliest collapsed gas clouds were small, about 105 solar
masses, and had a temperature of a few hundred Kelvin. The thermal
excitation of H2 molecules provides the microscopic mechanism
for the further radiative cooling, which might have led to the formation
of the first minigalaxies and/or quasars. If sufficient quantities of
H2 molecules were present, then the first stars and black
holes were born very early, at a redshift z ∼ 20 i.e., some
12 billion years ago, when the characteristic size of the Universe was
z + 1 times smaller than it is at present). If the dominant
radiative cooling mechanism was the excitation of the atomic hydrogen,
then the first objects with nearly 108 solar masses were
formed at a temperature of 104 K. The first galaxies appeared
in this case only for a redshift z ∼ 10. One
expects that astronomical surveys of the coming years will be able to
reach the distance that can be calculated from the Hubble law d
= H/v, where the Hubble parameter H was
defined in Sect. 2.1.4. The exploration of this
distance scale should bring evidence for the existence of the first
galaxies. According to the latest WMAP results
(Komatsu et
al. 2009)
the first galaxies were formed at z = 10.8 ± 1.4.
The Millenium simulation
(Springel et
al. 2005)
is an N-body
simulation tracing over 10 billion mass points, representing fractions
of the primordial gas, from the time of the CMBR decoupling to the
present-day Universe. This simulation showed that it was necessary to
assume cold dark matter (consisting of slowly moving, heavy particles)
to reproduce the large-scale structures found in galactic surveys. It
was also able to show that bright quasars are formed already at very
early stages, thus confirming the observational results from the Sloane
Digital Sky Survey
(Anderson et
al. 2001;
Abazajian et
al. 2009)
that challenged traditional models of structure formation.
The radiative cooling and further gravitational evolution of the
collapsed clouds lead to the appearance of the first stars (see
Sect. 4.1.1).
Particle families
Matter constituents (each has its own anti-particle)
Interaction vector particles
1st
(uL, dL), uR, dR
(eL, veL), eR
8 gluons
2nd
(cL, sL), cR, sR
Photon (γ)
(μL, vμL), μR
Weak quanta (Z0, W±)
3rd
(tL, bL), tR, bR
(τL, vτL), τR